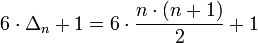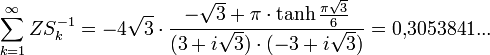Hexazahl

37 Kugeln in Form ineinandergeschachtelter Sechsecke

Eine zentrierte Sechseckszahl oder Hexzahl ist ein Zahl, die sich nach der Formel

3n² + 3n + 1

aus einer natürlichen Zahl n berechnen lässt. Die ersten zentrierten Sechseckszahlen sind

1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, … (Folge A003215 in OEIS)

Eine zentrierte Sechseckszahl beziffert eine Anzahl von Kreisen, so dass ein Kreis in der Mitte so gleichmäßig von Kreisen umgeben ist, das diese ein regelmäßiges Sechseck bilden. Sie gehören zu den zentrierten Polygonalzahlen, also auch zu den figurierte Zahlen.

Beziehungen zu anderen figurierten Zahlen

Kubikzahlen

Die Summe der ersten n zentrierten Sechseckzahlen ZS_i ergibt die n-te Kubikzahl K_n:

1 = 1 ; 1 + 7 = 8 ; 1 + 7 + 19 = 27 ; 1 + 7 + 19 + 37 = 64 ; ...

$K_n=ZS_1+ZS_2+\ldots +ZS_n$

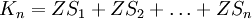
Quadratzahlen

Wenn man die Gleichung 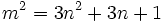$m^2 = 3n^2 + 3n + 1\$ löst, kann man zentrierte Sechseckzahlen finden, die auch Quadratzahlen sind, wie zum Beispiel 169 und 32761.

Dreieckzahlen

Die n-te zentrierte Sechseckszahl lässt sich auch nach der Formel

$6 \cdot \Delta_n + 1 =6 \cdot \frac{n\cdot (n+1)}{2} + 1$

mit Hilfe der n-ten Dreieckszahl Δ_n berechnen.

Wenn man die Gleichung 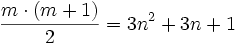$\frac{m\cdot (m+1)}{2} = 3n^2 + 3n + 1\$ löst, kann man zentrierte Sechseckszahlen finden, die auch Dreieckzahlen sind, wie zum Beispiel: 91, 8911 und 873181.

Summe der Kehrwerte

Die Summe der Kehrwerte der zentrierten Sechseckszahlen ist konvergent: Es gilt

$\sum_{k=1}^{\infty} ZS_{k}^{-1} = -4\sqrt{3} \cdot \frac{-\sqrt{3}+ \pi \cdot \tanh{\frac{\pi \sqrt{3}}{6}}}{(3+i\sqrt{3})\cdot (-3+i\sqrt{3})} = 0{,}3053841...$

Weblinks

• Eric W. Weisstein: Zentrierte Sechseckszahl auf MathWorld (englisch)