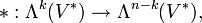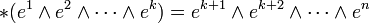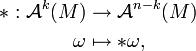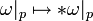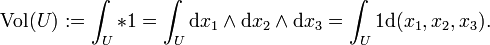Hodge-Operator

Der Hodge-Stern-Operator oder kurz Hodge-Operator ist ein Objekt aus der Differentialgeometrie. Es wurde von dem britischen Mathematiker William Vallance Douglas Hodge eingeführt. Der Operator ist ein Isomorphismus, welcher auf der äußeren Algebra eines endlichdimensionalen Prähilbertraums operiert oder allgemeiner auf dem Raum der Differentialformen.

Motivation

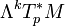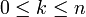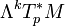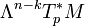Sei M eine n-dimensionale, glatte Mannigfaltigkeit und sei $\Lambda^k T^*_p M$ die k-te äußere Potenz des Kotangentialraums. Für alle k mit $0 \leq k \leq n$ haben die Vektorräume $\Lambda^k T^*_p M$ und $\Lambda^{n-k} T^*_p M$ dieselbe Dimension und sind deshalb isomorph. Hat M nun zusätzlich noch die Struktur einer orientierten, riemannschen Mannigfaltigkeit, so kann man beweisen, dass dieser Isomorphismus natürlich ist. Das heißt, er ist unabhängig von der Wahl der Basis. Die Verallgemeinerung dieses Isomorphismus auf das Tangentialbündel heißt Hodge-Stern-Operator.

Definition

Da der Raum 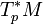$T^*_pM$ aus der obigen Motivation ein endlich-dimensionaler Vektorraum ist, beginnen wir mit der Definition des Hodge-Stern-Operators auf Vektorräumen.

Hodge-Stern-Operator auf Vektorräumen

Sei V ein n-dimensionaler Vektorraum mit Skalarprodukt und V ^* sein Dualraum. Wir bezeichnen mit 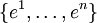$\{e^1, \ldots , e^n\}$ eine Orthonormalbasis des dualen Vektorraums. Betrachte die äußere Algebra Λ(V ^* ) dieses Raumes. Sei 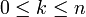$0 \leq k \leq n$, so induziert der Hodge-Stern-Operator einen kanonischen Isomorphismus

$* : \Lambda^k(V^*) \rightarrow \Lambda^{n-k}(V^*),$

welcher durch

$*(e^1\wedge e^2\wedge \cdots \wedge e^k)= e^{k+1}\wedge e^{k+2}\wedge \cdots \wedge e^n$

vollständig beschrieben wird. Der Raum Λ^k(V ^* ) heißt k-te äußere Potenz von V ^* .

Globaler Hodge-Stern-Operator

Nach dieser Vorarbeit kann man den Hodge-Stern-Operator auf die äußere Algebra des Kotangentialbündels 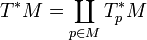$T^*M = \coprod_{p \in M}^{\ } T_p^*M$ übertragen. Wie in der Motivation sei M wieder eine orientierbare, glatte, riemannsche Mannigfaltigkeit. Außerdem setze 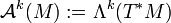$\mathcal{A}^k(M) := \Lambda^k(T^*M)$. Diese Menge nennt man den Raum der Differentialformen. Da T ^* M kein Vektorraum ist, wird der Operator punktweise definiert.

Der Hodge-Stern-Operator ist ein Isomorphismus

$\begin{align} *:\mathcal{A}^{k}(M) &\to \mathcal{A}^{n-k}(M)\\ \omega &\mapsto *\omega, \end{align}$

so dass für jeden Punkt $p \in M$

$\omega|_p \mapsto *\omega|_p$

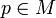
gilt. Die Differentialform ω, ausgewertet an der Stelle p, ist wieder ein Element eines Vektorraums, und damit greift obige Definition für Vektorräume. In dieser verallgemeinerten Definition wurde impliziert, dass die Form * ω wieder eine glatte Differentialform ist. Dies jedoch ist nicht klar und bedarf eines Beweises.

Riemannsche Volumenform

Sei M eine glatte, orientierte, riemannsche Mannigfaltigkeit. Fasst man dann 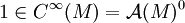$1 \in C^\infty(M) = \mathcal{A}(M)^0$ als konstante Einsfunktion auf, so ist die riemannsche Volumenform definiert als * 1. Diese Volumenform ist wichtiger Bestandteil der Integration mit Differentialformen. Das soll an einem einfachen Beispiel illustriert werden. Sei dafür 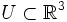$U \subset \R^3$ eine kompakte Teilmenge. Für das Volumen von U gilt 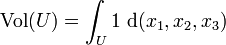$\mathrm{Vol}(U) = \int_U 1\ \mathrm{d}(x_1, x_2, x_3)$. Fasst man nun 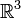$\R^3$ als eine Mannigfaltigkeit und U als eine darin enthaltene kompakte Teilmenge auf, so ist das Volumen in diesem Fall definiert als

$\operatorname{Vol}(U) := \int_U *1 = \int_U \mathrm{d}x_1 \wedge \mathrm{d}x_2 \wedge \mathrm{d} x_3 = \int_U 1 \mathrm{d} (x_1, x_2, x_3).$

Die Integrationstheorie auf Mannigfaltigkeiten beinhaltet also auch die Integration auf reellen Teilmengen. Nach diesem Prinzip kann man auch Funktionen auf Mannigfaltigkeiten integrieren, indem man diese mit der Volumenform multipliziert. Auf abstrakten Mannigfaltigkeiten muss man jedoch die Kartenwechsel beachten.

Siehe auch: Volumenform

Eigenschaften des Hodge-Stern-Operators

Sei M eine orientierte, glatte, riemannsche Mannigfaltigkeit, seien 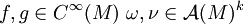$f,g \in C^\infty(M)\ \omega, \nu \in \mathcal{A}(M)^k$, und sei 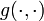$g(\cdot,\cdot)$ eine riemannsche Metrik. Dann hat der Hodge-Stern-Operator folgende Eigenschaften:

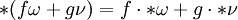1. $*(f \omega + g \nu) = f \cdot *\omega + g \cdot *\nu$ (Linearität),
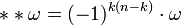2. $**\omega = (-1)^{k(n-k)} \cdot \omega$ (Bijektivität),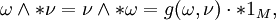
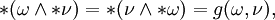
3. $\omega \wedge * \nu = \nu \wedge *\omega = g(\omega , \nu) \cdot *1_M,$
4. $*(\omega \wedge * \nu) = *(\nu \wedge * \omega) = g(\omega, \nu),$
5. g( * ω, * ν) = g(ω,ν) (Isometrie).

Literatur

• R. Abraham, J. E. Marsden, T. Ratiu: Manifolds, Tensor Analysis, and Applications. Springer-Verlag, Berlin 2003, ISBN 3-540-96790-7.
• S. Morita: Geometry of Differential Forms. American Mathematical Society, ISBN 0-821-81045-6.