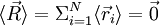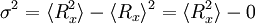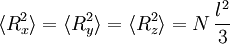- Ideale Kette
-
Das Modell der idealen Kette (Modell der Gauss'schen Kette, Modell der Frei beweglichen Kette) ist das einfachste Modell, das ein Polymer beschreibt. Es nimmt das Polymer lediglich als Random Walk an und vernachlässigt Interaktionen jeder Art zwischen den Monomeren - die sogar denselben Platz im Raum einnehmen können. Trotz seiner Einfachheit gibt dieses Modell einen guten Eindruck des Verhaltens von Polymeren. Genauer ist das Wormlike-Chain-Modell, bei dem die Annahmen realistischer sind.
Ein Polymer wird in diesem Modell als eine Kette von N steifen Stücken der Länge l (Kuhn-Länge) dargestellt - die maximale Länge ist also :
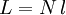 . Die Teilstücke sind "scharnierartig" beweglich, es ergibt sich also ein Random Walk mit der Schrittlänge l und der Schrittzahl N. Für große N gilt der Zentrale Grenzwertsatz.
. Die Teilstücke sind "scharnierartig" beweglich, es ergibt sich also ein Random Walk mit der Schrittlänge l und der Schrittzahl N. Für große N gilt der Zentrale Grenzwertsatz.In diesem simplen Ansatz werden keine Wechselwirkungen zwischen den Monomeren angenommen, die Energie des Polymers wird als unabhängig von seiner Form angenommen. Das bedeutet, im thermodynamischen Gleichgewicht sind alle denkbaren Konfigurationen gleich wahrscheinlich, das Polymer durchläuft sie alle im Laufe der Zeit - die Fluktuationen werden durch die Maxwell-Boltzmann-Verteilung beschrieben.
Sei
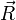 der End-zu-End-Vektor der idealen Kette und
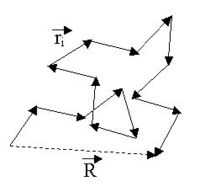
der End-zu-End-Vektor der idealen Kette und 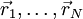 die Vektoren zu einzelnen Monomeren. Diese zufallsverteilten Vektoren haben drei Komponenten in x-, y- und z-Richtung. Wir nehmen an, die Zahl der Monomere N sei groß, so dass der Zentrale Grenzwertsatz gilt. Die Abbildung unten zeigt die Skizze einer kurzen idealen Kette:
die Vektoren zu einzelnen Monomeren. Diese zufallsverteilten Vektoren haben drei Komponenten in x-, y- und z-Richtung. Wir nehmen an, die Zahl der Monomere N sei groß, so dass der Zentrale Grenzwertsatz gilt. Die Abbildung unten zeigt die Skizze einer kurzen idealen Kette:Die Enden der Kette fallen nicht zusammen, aber da sie frei fluktuieren gilt natürlich für den Mittelwert (Erwartungswert):
Da
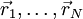 statistisch unabhängig sind, folgt aus dem Zentralen Grenzwertsatz, dass
statistisch unabhängig sind, folgt aus dem Zentralen Grenzwertsatz, dass 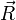 normal verteilt sind: genauer gesagt folgen in 3D Rx,Ry, und Rz gemäß einer Normalverteilung des Mittelwertes 0 mit Varianz:
normal verteilt sind: genauer gesagt folgen in 3D Rx,Ry, und Rz gemäß einer Normalverteilung des Mittelwertes 0 mit Varianz:
Wikimedia Foundation.