- Inferentielle Varianz
-
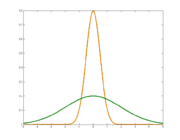 Dichten zweier normalverteilter Zufallsvariablen mit gleichem Erwartungswert aber unterschiedlichen Varianzen. Die orange Kurve hat eine geringere Varianz (entsprechend der Breite) als die grüne. Die Wurzel der Varianz, die Standardabweichung, kann bei der Normalverteilung an den Wendepunkten ersehen werden.
Dichten zweier normalverteilter Zufallsvariablen mit gleichem Erwartungswert aber unterschiedlichen Varianzen. Die orange Kurve hat eine geringere Varianz (entsprechend der Breite) als die grüne. Die Wurzel der Varianz, die Standardabweichung, kann bei der Normalverteilung an den Wendepunkten ersehen werden.Die Varianz ist ein Maß, das beschreibt, wie stark eine Messgröße (genauer eine Zufallsgröße) „streut“. Sie wird berechnet, indem man die Abstände der Messwerte vom Mittelwert quadriert, addiert und durch die Anzahl der Messwerte teilt.
In der Stochastik ist die Varianz ein Streuungsmaß, d. h. ein Maß für die Abweichung einer Zufallsvariable X von ihrem Erwartungswert
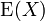 . Die Varianz verallgemeinert das Konzept der Summe der quadrierten Abweichungen vom Mittelwert in einer Beobachtungsreihe. Die Varianz der Zufallsvariable X wird üblicherweise als
. Die Varianz verallgemeinert das Konzept der Summe der quadrierten Abweichungen vom Mittelwert in einer Beobachtungsreihe. Die Varianz der Zufallsvariable X wird üblicherweise als 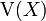 ,
, 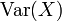 oder σ2 notiert. Ihr Nachteil für die Praxis ist, dass sie eine andere Einheit als die Daten besitzt. Dieser Nachteil kann behoben werden, indem man statt der Varianz die Standardabweichung benutzt. Die Standardabweichung ist die Quadratwurzel der Varianz. Eine einheitenlose Kennzahl für die Varianz ist der Variationskoeffizient, er macht auch die Varianz von Größen unterschiedlicher Einheit vergleichbar.
oder σ2 notiert. Ihr Nachteil für die Praxis ist, dass sie eine andere Einheit als die Daten besitzt. Dieser Nachteil kann behoben werden, indem man statt der Varianz die Standardabweichung benutzt. Die Standardabweichung ist die Quadratwurzel der Varianz. Eine einheitenlose Kennzahl für die Varianz ist der Variationskoeffizient, er macht auch die Varianz von Größen unterschiedlicher Einheit vergleichbar.In der Praxis ist die Varianz der Grundgesamtheit häufig nicht bekannt. Sie muss dann mit einem Varianzschätzer, etwa der Stichprobenvarianz geschätzt werden.
Inhaltsverzeichnis
Definition
Wenn
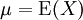 der Erwartungswert der quadratisch integrierbaren Zufallsvariablen X ist, dann berechnet sich die Varianz sowohl für diskrete als auch stetige Zufallsvariablen zu
der Erwartungswert der quadratisch integrierbaren Zufallsvariablen X ist, dann berechnet sich die Varianz sowohl für diskrete als auch stetige Zufallsvariablen zuDie Varianz ist also das zweite zentrale Moment einer Zufallsvariablen.
Die Varianz ist der Durchschnitt der Abweichungsquadrate vom Durchschnitt eines statistischen Merkmals.
Die Quadratwurzel der Varianz heißt Standardabweichung (σ):
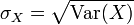 bzw.
bzw. 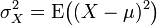
Rechenregeln
Verschiebungssatz
Lineare Transformation
dies kann mittels des Verschiebungssatzes hergeleitet werden:
Varianz von Summen von Zufallsvariablen
Hierin ist Cov(Xi,Xj) die Kovarianz der Größen Xi und Xj.
Sind die Zufallsvariablen paarweise unabhängig, so sind die Kovarianzen gleich Null und damit gilt:
Charakteristische Funktion
Die Varianz lässt sich mit dem Verschiebungssatz und der charakteristischen Funktion
 der Zufallsvariablen X darstellen als:
der Zufallsvariablen X darstellen als:Momenterzeugende Funktion
Da zwischen der charakteristischen und der momenterzeugenden Funktion der Zusammenhang
gilt, lässt sich die Varianz auch in dieser Form ohne die Verwendung komplexer Zahlen abbilden: (Zur obigen Berechnung von
 wird immer
wird immer 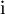 benötigt.)
benötigt.)Beispiele
Diskrete Zufallsvariable
Gegeben ist eine diskrete Zufallsvariable X mit den Wahrscheinlichkeiten
i 1 2 3 xi -1 1 2 f(xi) 0,5 0,3 0,2 wobei der Erwartungswert
beträgt.
Die Varianz ist demnach
Mit dem Verschiebungssatz erhält man entsprechend
Für die Standardabweichung ergibt sich damit
Stetige Zufallsvariable
Eine stetige Zufallsvariable habe die Dichtefunktion
Mit dem Erwartungswert
berechnet sich die Varianz mit Hilfe des Verschiebungssatzes als
Weblinks
Wikimedia Foundation.

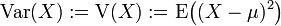
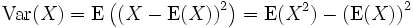
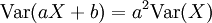
![\begin{align}
\operatorname{Var}(aX+b) &=
\operatorname{E}[ (aX + b - \operatorname{E}(aX + b))^2 ] =
\operatorname{E}[ (aX + b - b - a \operatorname{E}(X))^2 ]\\
&=
\operatorname{E}[ a^2 (X - \operatorname{E}(X))^2 ] =
a^2 \operatorname{E}[ (X - \operatorname{E}(X))^2 ] =
a^2 \operatorname{Var}(X)
\end{align}](/pictures/dewiki/56/8e802a24d50be0210f7e4693dfa85118.png)
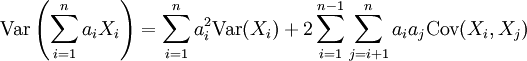
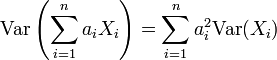
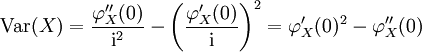
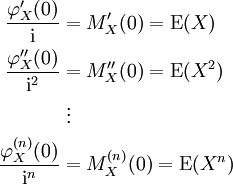
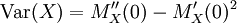
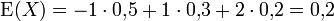
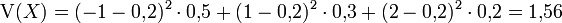
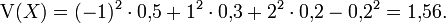
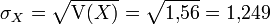
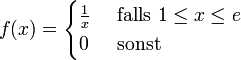
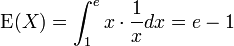
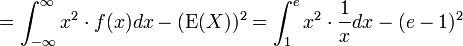
![\qquad = \left[ \frac{x^2}{2}\right] _1^e - (e - 1)^2 = \frac{e^2}{2} - \frac{1}{2} -(e-1)^2 \approx 0{,}242](/pictures/dewiki/57/9ce4f308f7cde58bcf097f9e26f2feba.png)