- Infix-Notation
-
Die allgemein gebräuchliche Schreibweise von Rechenoperationen und formalen logischen Ausdrücken wird als Infixnotation bezeichnet, da sie die Operatoren zwischen die Operanden setzt. Zum Beispiel:
1 + 2 · 8 ÷ 12
Allerdings kann diese Darstellung zu Verwirrung führen, da das Ergebnis von der Reihenfolge der Abarbeitung der Rechenoperationen abhängen kann. Bei o. g. Beispiel sind z. B. folgende Abarbeitungen denkbar:
- von links nach rechts
1 + 2 = 3 3 · 8 = 24 24 ÷ 12 = 2
- Punkt- vor Strich-Rechnung (allgemein gebräuchliche Form)
2 · 8 = 16 16 ÷ 12 = 1,333... 1 + 1,333... = 2,333...
Doch auch da gibt es noch Mehrdeutigkeiten, zum Beispiel bei 1÷2·3:
- von rechts nach links als 1÷(2·3):
2 · 3 = 6 1 ÷ 6 = 0,1666...
- von links nach rechts als (1÷2)·3 (allgemein gebräuchliche Form)
1 ÷ 2 = 0,5 0,5 · 3 = 1,5
Man hat sich deshalb bei der Infixnotation auf bestimmte Regeln zur Abarbeitung komplexerer Rechenoperationen geeinigt. Diese legen Prioritäten für einzelne Operatoren-Gruppen fest. So wird zum Beispiel Punktrechnung (Multiplikation, Division) vor der Strichrechnung (Addition, Subtraktion) ausgeführt. Treffen mehrere Punktrechnungen oder mehrere Strichrechnungen aufeinander, dann werden sie von links nach rechts ausgewertet; man sagt, die betroffenen Operatoren sind linksassoziativ.
Noch vor den Punktrechnungen werden Potenzierungen ausgewertet, sodass z.B.
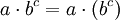 ist. Die Potenzierung ist zudem rechtsassoziativ, wird also im Gegensatz zu Punkt- und Strichrechnungen von rechts nach links ausgewertet. Das bedeutet, dass zum Beispiel der Ausdruck
ist. Die Potenzierung ist zudem rechtsassoziativ, wird also im Gegensatz zu Punkt- und Strichrechnungen von rechts nach links ausgewertet. Das bedeutet, dass zum Beispiel der Ausdruck 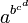 als
als 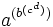 gelesen werden muss.
gelesen werden muss.Um die solcherart vordefinierte Operatorrangfolge zu verändern, benutzt man unterschiedliche Arten von Gliederungszeichen, wie die hier schon verwendeten Klammern. Mehr zum Thema der Gliederungszeichen siehe Operatorrangfolge: Gliederungszeichen.
Siehe auch
- Mehr und tiefergehende Informationen finden sich in den Artikeln Operatorrangfolge und Operatorassoziativität.
- Einige andere Notationen sind in den Artikeln Präfixnotation, Postfixnotation, Begriffsschriftnotation, Existential Graphs beschrieben.
Wikimedia Foundation.
