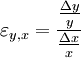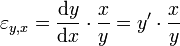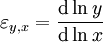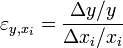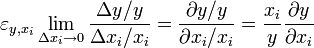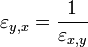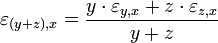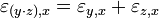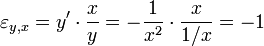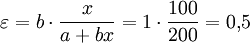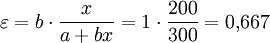Inverse Nachfrageelastizität

In den Wirtschaftswissenschaften ist eine Elastizität ein Maß, das die relative Änderung einer abhängigen Variablen auf eine relative Änderung einer ihrer unabhängigen Variablen angibt. ^[1] Nicht ganz korrekt, aber anschaulich ist dabei folgende Fragestellung: Um wieviel Prozent verändert sich eine Variable y als Reaktion auf die einprozentige Änderung der anderen Variable x? Man nennt diese relative Änderung die Elastizität von y bezüglich x oder die x-Elastizität von y.

Betrachtet man beispielsweise die relative Änderung der Nachfrage bei einer relativen Änderung des Preises, ist das die Nachfrageelastizität bezüglich des Preises oder die Preiselastizität der Nachfrage, auch kurz Preiselastizität genannt.

Die Motivation für die Verwendung der Elastizität ergibt sich daraus, dass die absolute Änderung der abhängigen Variablen nur unzureichend über die Struktur der Reaktion informiert.

Es wird beispielsweise ein Produkt betrachtet, dessen Preis um 1 € erhöht wird, worauf der Absatz um 10.000 Stück sinkt. Anhand der absoluten Größen lässt sich nur wenig über die Reichweite der Nachfrageänderung erkennen. Es fehlt der Vergleichmaßstab: Betrug der Preis im Ausgangspunkt 10 oder 100 €? Ist der Absatz von 50.000 auf 40.000 oder von 1.000.000 auf 990.000 Stück gesunken? Ein sinnvolles Maß für die Wirkung eines Instruments ist dagegen die Elastizität, die von relativen Änderungen ausgeht. Da die Elastizität keine Dimension - wie „€“ oder „Stück“ - enthält, ermöglicht sie die Vergleichbarkeit von gleichartigen Werten.

Mathematische Darstellung

Eine unabhängige Variable x

Um diese Verbaldefinition mathematisch zu fassen, betrachtet man eine Funktion $y = f(x)\,$.

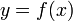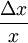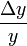Analog zum Konzept des Differenzenquotienten als Hinführung zum Differentialquotienten wird zunächst von der so genannten Bogenelastizität ausgegangen. Man betrachtet eine endlich kleine Änderung Δx der Variablen x und Δy der Variablen y, so dass sich die relativen Änderungen $\frac{\Delta x}{x}$ und $\frac{\Delta y}{y}$ ergeben. Die durchschnittliche relative Änderung von y in Bezug auf eine relative Änderung von x gibt die Bogenelastizität

• $\varepsilon_{y,x} = \frac{\frac{\Delta y}{y}}{\frac{\Delta x}{x}}$

an. Lässt man 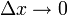$\Delta x \rightarrow 0$ gehen, erhält man als infinitesimale Auffassung die Elastizitätsfunkion von y bezüglich x

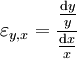• $\varepsilon_{y,x} = \frac{\frac{\mathrm dy}{y}}{\frac{\mathrm dx}{x}}$, die sich auch als

• $\varepsilon_{y,x} = \frac{\mathrm dy}{\mathrm dx} \cdot \frac{x}{y} = y' \cdot \frac{x}{y}$

darstellen lässt, für alle Werte von y, wo keine Nullstelle vorliegt und wo die Funktion differenzierbar ist. Man bezeichnet diese Elastizität auch als Punktelastizität.

Es lässt sich zudem zeigen, dass sich die Elastizität auch darstellen lässt als

• $\varepsilon_{y,x} = \frac{\mathrm d \ln y}{\mathrm d \ln x}$

Mehrere unabhängige Variablen

Man betrachtet eine Funktion 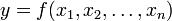$y = f(x_1, x_2, \dots, x_n)\,$, die von einer oder mehreren Einflussgrößen 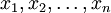$x_1, x_2, \dots, x_n\,$ abhängt. Eine Elastizität 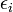$\epsilon_i\,$ gibt an, um welchen relativen Betrag 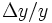$\Delta y/y\,$ sich ceteris paribus der Funktionswert 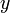$y\,$ ändert, wenn sich eine Einflussgröße um den relativen Betrag $\Delta x_i/x_i\,$ ändert. Damit ergibt sich für die Bogenelastizität

• $\varepsilon_{y,x_i} = \frac{\Delta y/y}{\Delta x_i / x_i}$

und bei infinitesimaler Betrachtung

• $\varepsilon_{y,x_i} \lim_{\Delta x_i\rarr0} \frac{\Delta y/y}{\Delta x_i / x_i} = \frac{\partial y/y}{\partial x_i/x_i} = \frac{x_i}{y} \frac{\partial y}{\partial x_i}$

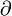wobei $\partial$ eine partielle Ableitung bezeichnet.

Mathematische Eigenschaften der Elastizität

Die Elastizität ist dimensionslos. Ihr Wertebereich ist die Menge der reellen Zahlen.

• $\varepsilon_{y,x} = \frac{1}{\varepsilon_{x,y}}$
• $\varepsilon_{(y+z),x} = \frac{y \cdot \varepsilon_{y,x}+ z \cdot \varepsilon_{z,x}}{y+z}$
• $\varepsilon_{(y\cdot z),x} = \varepsilon_{y,x} + \varepsilon_{z,x}$

Ökonomische Eigenschaften der Elastizität

Die Elastizität ist ein Maß für das Ausmaß der Reagibilität einer Funktion bezüglich einer Änderung des Abszissenwertes. Eine negative Elastizität bedeutet, dass die Funktion in dem betreffenden Bereich fällt.

Es lassen sich bezüglich der Elastizität folgende Erkenntnisse ableiten:

Wert von $\varepsilon$	Bezeichnung	Auswirkung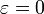
$\varepsilon = 0$	y ist vollkommen unelastisch.	y reagiert nicht auf eine Änderung von x.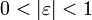
$0 < |\varepsilon| <1$	y ist unelastisch.	y ändert sich relativ weniger stark als x.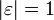
$|\varepsilon| = 1$	y ist proportional elastisch.	Die relative Änderung von y ist gleich der von x.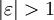
$|\varepsilon| > 1$	y ist elastisch.	y ändert sich relativ stärker als x.
$|\varepsilon| \rightarrow \infty$	y ist vollkommen elastisch.	Die relative Änderung von y ist unendlich hoch, selbst bei der kleinsten Änderung von x.

Alternative Bezeichnungsweisen

Eine Elastizität mit dem Wert 1 wird als proportional elastisch oder fließend bezeichnet. In der Literatur, wie z.B. in dem weitverbreiteten Lehrbuch von Varian "Grundzüge der Mikroökonomik" findet sich aber auch die die Bezeichnung "einheitselastisch" für eine Elastizität mit dem Absolutwert 1. Werte darunter werden als unterproportional elastisch bzw. unelastisch bezeichnet, während Werte darüber als überproportional elastisch bzw. elastisch bezeichnet werden.

Besonderheiten der Elastizität

Vollkommen unelastisch und vollkommen elastisch sind spezielle idealisierte Fälle.

Eine lineare Funktion, wie sie in den Wirtschaftswissenschaften häufig eingesetzt wird, hat in der Regel wie die meisten Funktionen an jedem Punkt eine andere Elastizität (Ausnahme: Ursprungsgeraden). Funktionen, die über ihren gesamten Definitionsbereich die gleiche Elastizität aufweisen, werden als Isoelastische Funktionen bezeichnet.

Beispiel für eine isoelastische Funktion

Die Elastizitätsfunktion von 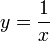$y = \frac{1}{x}$ ist isoelastisch, denn es ist

• $\varepsilon_{y,x} = y' \cdot \frac{x}{y} = -\frac{1}{x^2} \cdot \frac{x}{1/x}=-1$

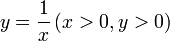$y = \frac{1}{x} \, (x >0, y > 0)$ könnte als Modell einer Preisabsatzfunktion interpretiert werden. In diesem Zusammenhang könnte man etwas salopp sagen, dass in allen Bereichen der Preisabsatzfunktion die Nachfrage um 1% fällt, wenn der Preis um 1% steigt.

Ein weiteres Beispiel für Isoelastizität ist eine Ursprungsgerade 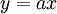$y = a x\,$ mit der Elastizität 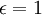$\epsilon = 1\,$. Eine sinnvolle Anwendung wäre eine Umsatzfunktion im polypolistischen Anbietermodell.

Ausgewählte Elastizitäten

In den Wirtschaftswissenschaften spielen unter anderem folgende Elastizitäten eine Rolle:

Elastizitäten in Bezug auf die unabhängige Variable

• Preiselastizitäten: Welchen Einfluss haben Preisänderungen auf Angebot und Nachfrage?
• Kreuzpreiselastizitäten: Welchen Einfluss haben Preisänderungen bei einem Gut auf Angebot und Nachfrage bei anderen Gütern?
• dynamische Preiselastizitäten: Welchen Einfluss hat eine gegenwärtige Preisänderung auf den zukünftigen Absatz?
• Einkommenselastizitäten: Welchen Einfluss haben Einkommensänderungen auf die Nachfrage nach einem Gut?
• Absatzwertelastizitäten: Welchen Einfluss haben Marketingaufwände auf die Nachfrage nach einem Gut?

Man unterscheidet beispielsweise bei der Preis- und Kreuzpreiselastizität noch zwischen Angebot und Nachfrage als abhängiger Variablen.

Verknüpfung

	Angebot als abhängige Variable	Nachfrage als abhängige Variable
Preis als unabhängige Variable	(direkte) Preiselastizität des Angebots: gibt an, wie stark das Angebot an einem Gut auf Veränderungen des eigenen Preises reagiert.	(direkte) Preiselastizität der Nachfrage: gibt an, wie stark die Nachfrage nach einem Gut auf Veränderungen des eigenen Preises reagiert.
Kreuzpreis als unabhängige Variable	Kreuzpreiselastizität des Angebots: gibt an, wie stark das Angebot an einem Gut auf Veränderungen des Preises bei einem Konkurrenzprodukt reagiert.	Kreuzpreiselastizität der Nachfrage: gibt an, wie stark die Nachfrage nach einem Gut auf Veränderungen des Preises eines anderen Produktes reagiert.
Einkommen als unabhängige Variable		Einkommenselastizität der Nachfrage: gibt an, wie stark die Nachfrage nach einem Gut auf Veränderungen des Einkommens reagiert.

Weitere ökonomische Elastizitäten

• Substitutionselastizität: gibt an, wie „leicht“ man bei einer gegebenen Produktionsfunktion und konstant gehaltenem Output einen Produktionsfaktor (z. B. Arbeit) durch einen anderen (z. B. Kapital) ersetzen kann. (Vergleiche beispielsweise die CES-Produktionsfunktion)
• Skalenelastizität, gibt an, wie stark der Output gesteigert werden kann, wenn die Einsatzmengen der Inputs ausgedehnt werden.
• Steuerbetragselastizität misst die Reaktion des Steuerbetrages (Aufkommen) bei einer relativen Veränderung der Bemessungsgrundlage.
• Zinselastizität gibt an, wie eine Zinsposition bei einer relativen Änderung des Zinssatzes reagiert.

Beispiele

Beispiel für eine lineare Funktion

Eine Gerade, die nicht vom Koordinatenursprung ausgeht, hat an jeder Stelle eine andere Elastizität, wie folgendes praktisches Beispiel zeigt.

Gegeben ist die lineare Funktion y = f(x) = x + 100. Es soll die Elastizität am Punkt x = 100 untersucht werden, d.h. die prozentuale Änderung von y, wenn x um ein Prozent erhöht wird.

Zu x = 100 gehört der Funktionswert y = f(100) = 100 + 100 = 200.

x wird um 1% erhöht: x + Δx = 100 + 1. Also erhält man für y = f(101) = 101 + 100 = 201.

Nach der 1%-igen Erhöhung von x ist der y-Wert von 200 auf 201 angewachsen. Er hat sich absolut um 1 erhöht, was einer prozentualen Änderung von 0,5% entspricht.

Unter Verwendung der Elastizitätsfunktion für eine Gerade y = a + bx, die angegeben werden kann als

• $\varepsilon = \frac{dy}{dx} \cdot \frac{x}{y} = y' \cdot \frac{x}{y} = b \cdot \frac{x}{a+bx}$,

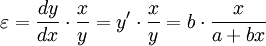würde sich für das Beispiel ergeben

• $\varepsilon = b \cdot \frac{x}{a+bx} = 1 \cdot \frac{100}{200} = 0{,}5$

wobei zu bemerken ist, dass die Elastizitätsfunktion bei positiver Steigung der Geraden und positivem Absolutglied a mit wachsendem x steigt. Bei a < 0 fällt sie streng monoton von 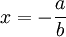$x = -\frac{a}{b}$ an von $\infty$ und strebt mit wachsendem x gegen 1.

Es wird nun die Elastizität für den Punkt x = 200 berechnet, der dem Funktionswert y = f(x) = f(200) = 200 + 100 = 300 entspricht. x wird um 1% erhöht, also absolut um 2. Es folgt y = f(x) = f(202) = 202 + 100 = 302. Die prozentuale Änderung ist dabei 2 / 300 = 0,00667, also 0,667%.

Die Ermittlung mit der Elastizitätsfunktion ergibt hier

• $\varepsilon = b \cdot \frac{x}{a+bx} = 1 \cdot \frac{200}{300} = 0{,}667$

Einzelnachweise

1. ↑ Anton Frantzke: Grundlagen der Volkswirtschaftslehre. Mikroökonomische Theorie und Aufgaben des Staates in der Marktwirtschaft, Schäffer-Poeschel, Stuttgart, 1999, S80

Quellen

Marketing-Planung auf der Basis von Reaktionsfunktionen (I) - Elastizitäten und Absatzreaktionsfunktionen, Karen Gedenk und Bernd Skiera, 1993/1994

Siehe auch

• Amoroso-Robinson-Relation