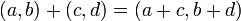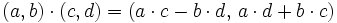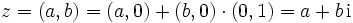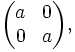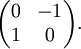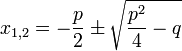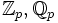- Irreelle Zahlen
-
ℂ
Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können.
Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als imaginäre Einheit bezeichnet. In der Elektrotechnik wird als Symbol statt i ein j benutzt, um eine Verwechslung mit dem Momentanwert der Stromstärke zu vermeiden.
Der Ursprung der Theorie der imaginären Zahlen, das heißt aller Zahlen, deren Quadrat eine negative reelle Zahl ist, geht auf die italienischen Mathematiker Gerolamo Cardano und Rafael Bombelli bis ins 16. Jahrhundert zurück. Die Einführung der imaginären Einheit i als neue Zahl wird Leonhard Euler zugeschrieben.
Komplexe Zahlen werden meist in der Form
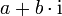 dargestellt, wobei a und b reelle Zahlen sind und i die imaginäre Einheit ist. Auf die so dargestellten komplexen Zahlen lassen sich die üblichen Rechenregeln für reelle Zahlen anwenden, wobei i2 stets durch −1 ersetzt werden kann und umgekehrt. Für die Menge der komplexen Zahlen wird das Symbol
dargestellt, wobei a und b reelle Zahlen sind und i die imaginäre Einheit ist. Auf die so dargestellten komplexen Zahlen lassen sich die üblichen Rechenregeln für reelle Zahlen anwenden, wobei i2 stets durch −1 ersetzt werden kann und umgekehrt. Für die Menge der komplexen Zahlen wird das Symbol  (Unicode: ℂ) verwendet.
(Unicode: ℂ) verwendet.Der so konstruierte Zahlenbereich der komplexen Zahlen bildet einen Körper und hat eine Reihe vorteilhafter Eigenschaften, die sich in vielen Bereichen der Natur- und Ingenieurwissenschaften als äußerst nützlich erwiesen haben. Einer der Gründe für diese positiven Eigenschaften ist die algebraische Abgeschlossenheit der komplexen Zahlen. Dies bedeutet, dass jede algebraische Gleichung vom Grad größer Null über den komplexen Zahlen eine Lösung besitzt, was für reelle Zahlen nicht gilt. Diese Eigenschaft ist der Inhalt des Fundamentalsatzes der Algebra. Ein weiterer Grund ist ein Zusammenhang zwischen trigonometrischen Funktionen und der Exponentialfunktion, der über die komplexen Zahlen hergestellt werden kann. Ferner ist jede einmal komplex differenzierbare Funktion von selbst beliebig oft differenzierbar, anders als in der Mathematik der reellen Zahlen. Die Eigenschaften von Funktionen mit komplexen Argumenten sind Gegenstand der Funktionentheorie, auch komplexe Analysis genannt.
Definition
Als komplexe Zahlen bezeichnet man die Zahlen der Form
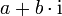 (bzw. in verkürzter Notation a + bi oder auch a + ib) mit reellen Zahlen a und b. Die imaginäre Einheit i ist dabei eine nicht-reelle Zahl mit der Eigenschaft i2 = − 1.
(bzw. in verkürzter Notation a + bi oder auch a + ib) mit reellen Zahlen a und b. Die imaginäre Einheit i ist dabei eine nicht-reelle Zahl mit der Eigenschaft i2 = − 1.Dabei wird a als Realteil und b als Imaginärteil von a + bi bezeichnet. Es haben sich zwei verschiedene Notationen dafür etabliert:
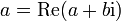 und
und 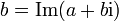 bzw.
bzw.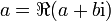 und
und 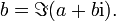
Eine formale Präzisierung wäre beispielsweise die folgende: Die komplexen Zahlen sind ein Körper
 , der die reellen Zahlen als Teilkörper enthält, zusammen mit einem Element
, der die reellen Zahlen als Teilkörper enthält, zusammen mit einem Element 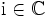 , das die Gleichung i2 = − 1 erfüllt, so dass sich jedes Element von
, das die Gleichung i2 = − 1 erfüllt, so dass sich jedes Element von  auf eindeutige Weise in der Form
auf eindeutige Weise in der Form 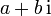 mit
mit 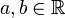 schreiben lässt. Zwei Paare
schreiben lässt. Zwei Paare 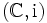 und
und 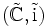 können auf eindeutige Weise miteinander identifiziert werden.
können auf eindeutige Weise miteinander identifiziert werden.Notation
Die Notation in der Form
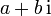 wird auch als (nach René Descartes benannte) kartesische oder algebraische Form bezeichnet. Die Bezeichnung kartesisch erklärt sich aus der Darstellung in der komplexen bzw. gaußschen Zahlenebene (s. weiter unten). Es findet sich auch die Darstellung
wird auch als (nach René Descartes benannte) kartesische oder algebraische Form bezeichnet. Die Bezeichnung kartesisch erklärt sich aus der Darstellung in der komplexen bzw. gaußschen Zahlenebene (s. weiter unten). Es findet sich auch die Darstellung 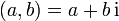 [1]; in der Norm DIN 1302:1999 "Allgemeine mathematische Zeichen und Begriffe" kommt sie allerdings nicht vor.
[1]; in der Norm DIN 1302:1999 "Allgemeine mathematische Zeichen und Begriffe" kommt sie allerdings nicht vor.In der Elektrotechnik wird das kleine i schon für zeitlich veränderliche Ströme verwendet (siehe Wechselstrom) und kann zu Verwechselungen mit der imaginären Einheit i führen. Daher wird in diesem Bereich gemäß DIN 1302 der Buchstabe j verwendet.
In der Physik wird zwischen
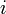 für Wechselstrom und
für Wechselstrom und 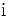 für die imaginäre Einheit unterschieden. Dies führt durch die recht klare Trennung beim aufmerksamen Leser nicht zu Verwechslungen und wird in dieser Form weitgehend sowohl in der physikalisch-experimentellen als auch in der physikalisch-theoretischen Literatur angewendet; handschriftlich ist diese Feinheit allerdings nicht zu halten. Siehe auch: komplexe Wechselstromrechnung
für die imaginäre Einheit unterschieden. Dies führt durch die recht klare Trennung beim aufmerksamen Leser nicht zu Verwechslungen und wird in dieser Form weitgehend sowohl in der physikalisch-experimentellen als auch in der physikalisch-theoretischen Literatur angewendet; handschriftlich ist diese Feinheit allerdings nicht zu halten. Siehe auch: komplexe WechselstromrechnungKomplexe Zahlen werden gemäß DIN 1304-1 und DIN 5483-3 unterstrichen dargestellt, um sie von reellen Zahlen zu unterscheiden. (Manche Autoren benutzen dies jedoch auch, um (Vierer-)Vektoren zu kennzeichnen.)
Rechnen in der algebraischen Form
Addition
Für die Addition zweier komplexer Zahlen
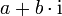 und
und 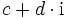 gilt
gilt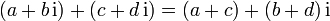 .
.
Subtraktion
Analog zur Addition (siehe oben) funktioniert auch die Subtraktion
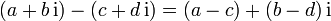 .
.
Multiplikation
Für die Multiplikation gilt entsprechend
 .
.
Diese Formel ergibt sich mit der Definition i2 = − 1 durch einfaches Ausmultiplizieren und Neugruppieren.
Division
Der Quotient zweier komplexer Zahlen
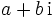 und
und 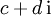 mit
mit 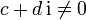 lässt sich berechnen, indem man den Bruch mit der zum Nenner
lässt sich berechnen, indem man den Bruch mit der zum Nenner 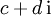 konjugiert komplexen Zahl
konjugiert komplexen Zahl 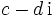 erweitert. Der Nenner wird dadurch reell (und ist gerade das Quadrat des Betrages von
erweitert. Der Nenner wird dadurch reell (und ist gerade das Quadrat des Betrages von  ):
):Rechenbeispiele
Addition:
Subtraktion:
Multiplikation:
Division:
Weitere Eigenschaften
- Der Körper
 der komplexen Zahlen ist einerseits ein Oberkörper von
der komplexen Zahlen ist einerseits ein Oberkörper von  , andererseits ein zweidimensionaler
, andererseits ein zweidimensionaler  -Vektorraum. Der Isomorphismus
-Vektorraum. Der Isomorphismus 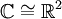 wird auch als natürliche Identifikation bezeichnet.
wird auch als natürliche Identifikation bezeichnet. - Die Körpererweiterung
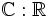 ist vom Grad
ist vom Grad ![[\Bbb C:\R]=2](/pictures/dewiki/100/de7c84b79a74a28bbdbb6e7ae62ba772.png) ; genauer ist
; genauer ist  isomorph zum Faktorring
isomorph zum Faktorring ![\R[X]/(X^2+1)](/pictures/dewiki/97/a9dc8e69251c016fa9403836e5f573b4.png) , wobei X2 + 1 das Minimalpolynom von i über
, wobei X2 + 1 das Minimalpolynom von i über  ist. Ferner bildet
ist. Ferner bildet  bereits den algebraischen Abschluss von
bereits den algebraischen Abschluss von  .
. - Als
 -Vektorraum besitzt
-Vektorraum besitzt  die Basis {1,i}. Daneben ist
die Basis {1,i}. Daneben ist  wie jeder Körper auch ein Vektorraum über sich selbst, also ein eindimensionaler
wie jeder Körper auch ein Vektorraum über sich selbst, also ein eindimensionaler  -Vektorraum mit Basis {1}.
-Vektorraum mit Basis {1}. - i und − i sind genau die Lösungen der quadratischen Gleichung x2 + 1 = 0. In diesem Sinne kann i (aber auch − i) als „Wurzel aus − 1“ aufgefasst werden.
 ist im Gegensatz zu
ist im Gegensatz zu  kein geordneter Körper, d. h., es gibt keine mit der Körperstruktur verträgliche lineare Ordnungsrelation „<“ auf
kein geordneter Körper, d. h., es gibt keine mit der Körperstruktur verträgliche lineare Ordnungsrelation „<“ auf  . Von zwei unterschiedlichen komplexen Zahlen kann man daher nicht sagen, welche von beiden die größere bzw. die kleinere Zahl ist.
. Von zwei unterschiedlichen komplexen Zahlen kann man daher nicht sagen, welche von beiden die größere bzw. die kleinere Zahl ist.
Komplexe Zahlenebene
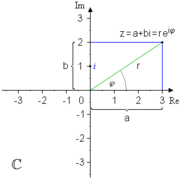 Gaußsche Ebene mit einer komplexen Zahl in kartesischen und in Polarkoordinaten
Gaußsche Ebene mit einer komplexen Zahl in kartesischen und in PolarkoordinatenWährend sich die Menge
 der reellen Zahlen durch Punkte auf einer Zahlengeraden veranschaulichen lässt, kann man die Menge
der reellen Zahlen durch Punkte auf einer Zahlengeraden veranschaulichen lässt, kann man die Menge  der komplexen Zahlen als Punkte in einer Ebene (komplexe Ebene, gaußsche Zahlenebene) darstellen. Dies entspricht der „doppelten Natur“ von
der komplexen Zahlen als Punkte in einer Ebene (komplexe Ebene, gaußsche Zahlenebene) darstellen. Dies entspricht der „doppelten Natur“ von  als zweidimensionalem reellem Vektorraum. Die Teilmenge der reellen Zahlen bildet darin die waagerechte Achse, die Teilmenge der rein imaginären Zahlen (d. h. mit Realteil 0) bildet die senkrechte Achse. Eine komplexe Zahl
als zweidimensionalem reellem Vektorraum. Die Teilmenge der reellen Zahlen bildet darin die waagerechte Achse, die Teilmenge der rein imaginären Zahlen (d. h. mit Realteil 0) bildet die senkrechte Achse. Eine komplexe Zahl 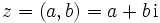 ,
, 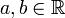 besitzt dann die horizontale Koordinate a und die vertikale Koordinate b.
besitzt dann die horizontale Koordinate a und die vertikale Koordinate b.Gemäß Definition entspricht die Addition komplexer Zahlen der Vektoraddition. Die Multiplikation ist in der gaußschen Ebene eine Drehstreckung, was nach Einführung der Polarform weiter unten klarer werden wird. Besonders in der Physik wird die geometrisch anschauliche Ebene häufig als die komplexe Zahlenebene aufgefasst und der Notation der komplexen Zahlen der Vorzug vor der Vektordarstellung gegeben.
Polarform
Verwendet man anstelle der kartesischen Koordinaten a und b die Polarkoordinaten
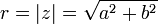 und
und  , so kann die komplexe Zahl
, so kann die komplexe Zahl 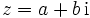 auch in der Form
auch in der Formdargestellt werden, da
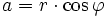 und
und 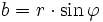 ist. Diese Darstellung einer komplexen Zahl heißt Polarform.
ist. Diese Darstellung einer komplexen Zahl heißt Polarform.Die Darstellung
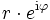 mit Hilfe der komplexen e-Funktion heißt Exponentialform, die Darstellung
mit Hilfe der komplexen e-Funktion heißt Exponentialform, die Darstellung 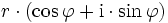 heißt trigonometrische Form.
heißt trigonometrische Form.Wegen der eulerschen Identität sind Exponentialform und trigonometrische Form bedeutungsgleich und stellen alternative Schreibweisen für die Polarform dar. Des weiteren gibt es für die Polarform auch die alternativen Schreibweisen
die einer vereinfachten Schreibung dienen. Statt Form werden auch die Bezeichnungen Darstellung oder Darstellungsform verwendet,
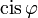 steht für
steht für  .
.In der komplexen Zahlenebene entspricht dabei r der euklidischen Vektorlänge (d. h. dem Abstand zum Ursprung 0) und
 dem mit der reellen Achse eingeschlossenen Winkel der Zahl z.
dem mit der reellen Achse eingeschlossenen Winkel der Zahl z.Üblicherweise wird r der Betrag oder Modul von z (Schreibweise r = | z | ) genannt,
 wird ein Argument (oder auch Winkel oder Phase) von z (Schreibweise
wird ein Argument (oder auch Winkel oder Phase) von z (Schreibweise 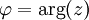 ) genannt. Da
) genannt. Da  und
und 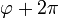 derselben Zahl zugeordnet werden können, ist die Polardarstellung zunächst nicht eindeutig. Deshalb schränkt man
derselben Zahl zugeordnet werden können, ist die Polardarstellung zunächst nicht eindeutig. Deshalb schränkt man  meist auf das Intervall ( − π;π] ein, also
meist auf das Intervall ( − π;π] ein, also 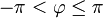 , und spricht dann von dem Argument (oder dem Hauptwert des Argumentes) von
, und spricht dann von dem Argument (oder dem Hauptwert des Argumentes) von 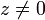 ; der Zahl 0 ließe sich jedes beliebige Argument zuordnen. Zum Zwecke einer eindeutigen Darstellung kann dieses beispielsweise auf 0 festgelegt werden.
; der Zahl 0 ließe sich jedes beliebige Argument zuordnen. Zum Zwecke einer eindeutigen Darstellung kann dieses beispielsweise auf 0 festgelegt werden.Das Argument ist auch der Imaginärteil des komplexen natürlichen Logarithmus
Mit der Wahl eines auf ganz
 definierten Zweiges des Logarithmus ist also auch eine Argumentfunktion bestimmt (und umgekehrt).
definierten Zweiges des Logarithmus ist also auch eine Argumentfunktion bestimmt (und umgekehrt).Alle Werte
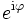 bilden den Einheitskreis der komplexen Zahlen mit dem Betrag 1.
bilden den Einheitskreis der komplexen Zahlen mit dem Betrag 1.Komplexe Konjugation
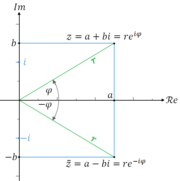 Eine komplexe Zahl z = a+bi mit ihrer konjugiert komplexen Zahl
Eine komplexe Zahl z = a+bi mit ihrer konjugiert komplexen Zahl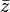 = a−bi
= a−biDreht man das Vorzeichen des Imaginärteils b einer komplexen Zahl
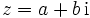 um, so erhält man die zu z konjugiert komplexe Zahl
um, so erhält man die zu z konjugiert komplexe Zahl 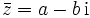 (manchmal auch z * geschrieben).
(manchmal auch z * geschrieben).Die Konjugation
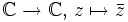 ist ein Körperautomorphismus (involutorischer Automorphismus), da sie mit Addition und Multiplikation verträglich ist, d. h., für alle
ist ein Körperautomorphismus (involutorischer Automorphismus), da sie mit Addition und Multiplikation verträglich ist, d. h., für alle 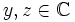 gilt
gilt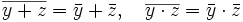 .
.
In der Polardarstellung hat die konjugiert komplexe Zahl
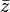 bei unverändertem Betrag gerade den negativen Winkel von z. Man kann die Konjugation in der komplexen Zahlenebene also als die Spiegelung an der reellen Achse identifizieren. Insbesondere werden unter der Konjugation genau die reellen Zahlen auf sich selbst abgebildet.
bei unverändertem Betrag gerade den negativen Winkel von z. Man kann die Konjugation in der komplexen Zahlenebene also als die Spiegelung an der reellen Achse identifizieren. Insbesondere werden unter der Konjugation genau die reellen Zahlen auf sich selbst abgebildet.Das Produkt aus einer komplexen Zahl z = a + bi und ihrer komplex Konjugierten
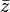 ergibt das Quadrat ihres Betrages:
ergibt das Quadrat ihres Betrages: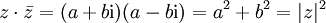 .
.
Die Summe aus einer komplexen Zahl z = a + bi und ihrer komplex Konjugierten
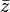 ergibt das 2-fache ihres Realteils:
ergibt das 2-fache ihres Realteils: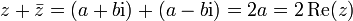 .
.
Die Differenz aus einer komplexen Zahl z = a + bi und ihrer komplex Konjugierten
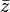 ergibt das 2i-fache ihres Imaginärteils:
ergibt das 2i-fache ihres Imaginärteils: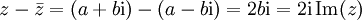 .
.
Umrechnungsformeln
Von der algebraischen Form in die Polarform
Für
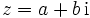 in algebraischer Form ist
in algebraischer Form istFür z = 0 kann das Argument mit 0 definiert werden.
Für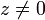 kann das Argument
kann das Argument  mit Hilfe des Arkustangens wie folgt im Intervall ( − π;π] bestimmt werden:
mit Hilfe des Arkustangens wie folgt im Intervall ( − π;π] bestimmt werden:Die Berechnungsvariante über den Arcustangens benötigt relativ umständliche Fallunterscheidungen, da der Sonderfall a = 0 gesondert behandelt werden muss und da der Tangens denselben Wert zweimal im Intervall [0,2π] annimmt. Die neueren Programmiersprachen stellen aber meist eine Variante der Arkustangensfunktion zur Verfügung, die den Wert je nach Vorzeichen von a und b dem passenden Quadranten zuordnet (häufig mit dem Namen atan2 bezeichnet).
Mit Hilfe des Arkuskosinus kommt man mit nur drei Fallunterscheidungen aus:
Berechnung des Winkels im Intervall [0, 2π)
Die Berechnung des Winkels φ' im Intervall [0, 2π) kann im Prinzip so durchgeführt werden, dass der Winkel zunächst wie vorstehend beschrieben im Intervall (−π, π] berechnet wird und dann um 2π vergrößert wird, falls er negativ ist:
(siehe Polarkoordinaten)
Von der Polarform in die algebraische Form
Wie weiter oben, stellt a den Realteil und b den Imaginärteil jener komplexen Zahl dar.
Multiplikation und Division in der Polarform
Bei der Multiplikation in der Polarform werden die Beträge multipliziert und die Phasen addiert. Bei der Division wird der Betrag des Dividenden durch den Betrag des Divisors geteilt und die Phase des Divisors von der Phase des Dividenden subtrahiert:
Trigonometrische Form
Exponentialform
Rechenoperationen 3. Stufe
Zu den Rechenoperationen der dritten Stufe gehören Potenzieren, Radizieren, also Wurzelziehen und das Logarithmieren.
Potenzen
Natürliche Exponenten
Die n-te Potenz berechnet sich in der polaren Form
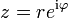 zu
zuoder für die algebraische Form z = a + bi zu
Beliebige komplexe Exponenten
Die allgemeine Definition einer Potenz mit komplexer Basis und komplexem Exponent lautet
wobei ln(z) für den Hauptwert des komplexen Logarithmus steht (siehe unten)
Wurzeln
- Hauptartikel: Wurzel (Mathematik)
Beim Rechnen mit Wurzeln ist größte Vorsicht angebracht, da die bekannten Rechenregeln für nichtnegative reelle Zahlen hier nicht gelten. Egal, welchen der beiden möglichen Werte i oder − i man für
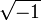 festlegt, erhält man z. B.
festlegt, erhält man z. B.Bei der Berechnung der n-ten Wurzel der komplexen Zahl z = reiφ dient die Formel
wobei k die Werte
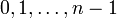 durchläuft. Eine Zahl hat also n komplexe n-te Wurzeln.
durchläuft. Eine Zahl hat also n komplexe n-te Wurzeln.Logarithmen
Der komplexe natürliche Logarithmus ist im Gegensatz zum Reellen nicht eindeutig. Man arbeitet daher mit Hauptwerten, d. h. Werten eines bestimmten Streifens der komplexen Ebene.
Der Hauptwert des natürlichen Logarithmus der komplexen Zahl z = reiφ ist
- lnz = lnr + iφ.
Pragmatische Rechenregeln
Am einfachsten lassen sich die Berechnungen folgendermaßen durchführen:
- Addition und Subtraktion komplexer Zahlen werden (in der algebraischen Form) komponentenweise durchgeführt.
- Die Multiplikation komplexer Zahlen kann je nach Vorgabe vorteilhaft in algebraischer Form oder in Exponentialform (Multiplikation der Beträge und Addition der Argumente (Winkel)) durchgeführt werden.
- Bei der Division komplexer Zahlen werden in Exponentialform ihre Beträge dividiert und ihre Argumente (Winkel) subtrahiert, oder in algebraischer Form mit dem konjugierten multipliziert und durch dessen Betragsquadrat dividiert.
- Beim Potenzieren einer komplexen Zahl mit einem reellen Exponenten wird ihr Betrag potenziert und ihr Argument (Winkel) mit dem Exponenten multipliziert; die Benutzung der algebraischen Form (mit Newtons Binomialsatz) ist, bis auf Ausnahmen, insbesondere für höhere Potenzen meist umständlicher.
- Beim Radizieren (Wurzelziehen) einer komplexen Zahl mit einem reellen Exponenten wird ihr Betrag radiziert und ihr Argument (Winkel) durch den Exponenten dividiert. Hierdurch entsteht die erste Lösung. Bei einer n-ten Wurzel entstehen n Lösungen, die im Winkel von 2π / n um den Ursprung der gaußschen Ebene verteilt sind. Siehe Wurzel (Mathematik). Eine Quadratwurzel kann auch recht einfach in kartesischer Form berechnet werden.
Konstruktion der komplexen Zahlen
Damit die obige axiomatische Definition einen Sinn hat, muss nachgewiesen werden, dass es überhaupt einen Körper
 mit den benötigten Eigenschaften gibt. Dies leisten die folgenden Konstruktionen.
mit den benötigten Eigenschaften gibt. Dies leisten die folgenden Konstruktionen.Paare reeller Zahlen
Die Konstruktion nimmt zunächst keinerlei Bezug auf die imaginäre Einheit i: Im 2-dimensionalen reellen Vektorraum
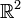 der geordneten reellen Zahlenpaare z = (a,b) wird neben der Addition
der geordneten reellen Zahlenpaare z = (a,b) wird neben der Addition(das ist die gewöhnliche Vektoraddition) eine Multiplikation durch
definiert.
Nach dieser Festlegung schreibt man
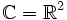 , und
, und 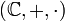 wird zu einem Körper, dem Körper der komplexen Zahlen.
wird zu einem Körper, dem Körper der komplexen Zahlen.Erste Eigenschaften
- Die Abbildung
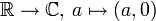 ist eine Körpereinbettung von
ist eine Körpereinbettung von  in
in  , aufgrund derer wir die reelle Zahl a mit der komplexen Zahl (a,0) identifizieren.
, aufgrund derer wir die reelle Zahl a mit der komplexen Zahl (a,0) identifizieren.
Bezüglich der Addition ist:
- die Zahl 0 = (0,0) das Nullelement in
 und
und - die Zahl − z = ( − a, − b) das inverse Element in
 .
.
Bezüglich der Multiplikation ist:
- die Zahl 1 = (1,0) das neutrale Element (das Einselement) von
 und
und - das Inverse (Reziproke) zu
 ist
ist 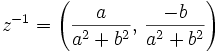 .
.
Bezug zur Darstellung in der Form a + bi
Durch i = (0,1) wird die imaginäre Einheit i festgelegt; für diese gilt i2 = − 1.
Jede komplexe Zahl
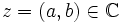 besitzt die eindeutige Darstellung der Form
besitzt die eindeutige Darstellung der Formmit
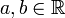 ; dies ist die übliche Schreibweise für die komplexen Zahlen.
; dies ist die übliche Schreibweise für die komplexen Zahlen.Polynome: Adjunktion
Eine weitere Konstruktion der komplexen Zahlen ist der Faktorring
des Polynomringes in einer Unbestimmten über den reellen Zahlen. Die Zahl i entspricht dabei dem Bild der Unbestimmten X, die reellen Zahlen werden mit den konstanten Polynomen identifiziert.
Dieses Konstruktionsprinzip ist auch in anderem Kontext anwendbar, man spricht von Adjunktion.
Matrizen
Die Menge der
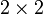 -Matrizen der Form
-Matrizen der Form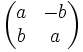 mit
mit 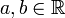
bildet ebenfalls ein Modell der komplexen Zahlen: Reelle Zahlen entsprechen Diagonalmatrizen
die Zahl i ist die Matrix
Die zu diesen Matrizen gehörenden linearen Abbildungen sind, sofern a und b nicht beide null sind, Drehstreckungen im Raum
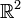 . Es handelt sich genau um dieselben Drehstreckungen wie bei der Interpretation der Multiplikation mit einer komplexen Zahl a + bi in der gaußschen Zahlenebene.
. Es handelt sich genau um dieselben Drehstreckungen wie bei der Interpretation der Multiplikation mit einer komplexen Zahl a + bi in der gaußschen Zahlenebene.Geschichtliches
Die Unmöglichkeit der oben angegebenen Lösung ist bei der Behandlung der quadratischen Gleichung schon sehr früh bemerkt und hervorgehoben worden, z. B. schon in der um 820 n. Chr. verfassten Algebra des Muhammed ibn Mûsâ Alchwârizmî. Aber bei dem nächstliegenden und unanfechtbaren Schluss, dass diese Art von Gleichung nicht lösbar ist, blieb man nicht stehen.
In gewissem Sinne ist bereits der Italiener Gerolamo Cardano (1501–1576) in seinem 1545 erschienenen Buch Artis magnae sive de regulis algebraicis liber unus darüber hinausgegangen. Er behandelt dort die Aufgabe, zwei Zahlen zu finden, deren Produkt 40 und deren Summe 10 ist. Er hebt hervor, dass die dafür anzusetzende Gleichung:
- x(10 − x) = 40 oder x2 − 10x + 40 = 0
keine Lösung hat, fügt aber einige Bemerkungen hinzu, indem er in die allgemeine Lösung der quadratischen Gleichung
für p und q die Werte (−10) und 40 einsetzt. Wenn es also möglich wäre, dem sich ergebenden Ausdruck
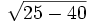 oder
oder 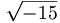
einen Sinn zu geben, und zwar so, dass man mit diesem Zeichen nach denselben Regeln rechnen dürfte, wie mit einer reellen Zahl, so würden die Ausdrücke
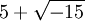 oder
oder 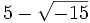
in der Tat eine Lösung darstellen.
Für die Quadratwurzel aus negativen Zahlen und allgemeiner für alle aus einer beliebigen reellen Zahl α und einer positiven reellen Zahl β zusammengesetzten Zahlen
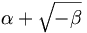 oder
oder 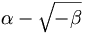
hat sich seit der Mitte des 17. Jahrhunderts die Bezeichnung imaginäre Zahl eingebürgert.
Im Gegensatz dazu wurden als gewöhnliche Zahlen die reellen Zahlen bezeichnet. Eine solche Gegenüberstellung der zwei Begriffe findet sich in der 1637 erschienenen La Géométrie von Descartes und taucht dort wohl zum ersten Mal auf.
Heute bezeichnet man nur noch den Ausdruck, der durch die Wurzel aus einer negativen Zahl gebildet wird, als imaginäre Zahl und die von beiden Arten von Zahlen gebildete Menge von Zahlen als komplexe Zahlen. Man kann daher sagen, dass Cardano zum ersten Mal im heutigen Sinne mit komplexen Zahlen gerechnet hat und damit eine Reihe von Betrachtungen angestellt hat.
Da das Rechnen mit diesen als „sinnlos“ angesehenen Zahlen zunächst als bloßes Spiel erschien, war man umso überraschter, dass dieses „Spiel“ sehr häufig wertvolle Ergebnisse lieferte oder schon bekannten Ergebnissen eine befriedigendere Form zu geben erlaubte. So kam Leonhard Euler zum Beispiel in seiner Introductio in analysin infinitorum zu einigen bemerkenswerten Gleichungen, die nur reelle Zahlen enthielten und sich ausnahmslos als richtig erwiesen, die aber auf anderem Wege nicht so einfach gewonnen werden konnten.
So kam es, dass man diese Zahlen nicht als widersinnig verwarf, sondern sich immer mehr mit ihnen beschäftigte. Trotzdem umgab dieses Gebiet der Mathematik noch immer etwas Geheimnisvolles, Rätselhaftes und Unbefriedigendes. Erst durch die Abhandlung Essai sur la représentation analytique de la direction aus dem Jahre 1797 des norwegisch-dänischen Landmessers Caspar Wessel (1745–1818) wurde die Aufklärung über diese Zahlen angebahnt. Diese Arbeit, die er bei der dänischen Akademie einreichte, fand anfangs keine Beachtung. Ähnlich erging es Arbeiten anderer Mathematiker, sodass diese Betrachtungen noch mehrfach angestellt werden mussten.
Als erster definierte Augustin Louis Cauchy 1821 in seinem Lehrbuch Cours d'analyse eine Funktion einer komplexen Variablen in die komplexe Zahlenebene und bewies viele grundlegende Sätze der Funktionentheorie.
Allgemeine Beachtung fanden sie erst dann, als auch Carl Friedrich Gauß im Jahre 1831 in einem Artikel in den Göttingschen gelehrten Anzeigen dieselben Auffassungen entwickelte, offensichtlich ohne Wissen von irgendwelchen Vorgängern.
Heute machen diese Dinge keinerlei begriffliche oder tatsächliche Schwierigkeiten. Durch die Einfachheit der Definition, der bereits erläuterten Bedeutung und Anwendungen in vielen Wissenschaftsgebieten stehen die komplexen Zahlen den reellen Zahlen in nichts nach. Der Begriff der „imaginären“ Zahlen, im Sinne von eingebildeten bzw. unwirklichen Zahlen, hat sich also im Laufe der Jahrhunderte als schiefe Auffassung erwiesen.
Anwendung
Die komplexen Zahlen in der Physik
Komplexe Zahlen spielen in der Grundlagenphysik eine zentrale Rolle. Sie finden dort Verwendung bei der Definition von Differentialoperatoren in der Schrödingergleichung und der Klein-Gordon-Gleichung. Für die Dirac-Gleichung benötigt man eine Zahlbereichserweiterung der komplexen Zahlen, die Quaternionen. Alternativ ist eine Formulierung mit Pauli-Matrizen möglich, die aber die gleiche algebraische Struktur wie die Quaternionen aufweisen.
Komplexe Zahlen haben in der Physik und Technik eine wichtige Rolle als Rechenhilfe. So lässt sich insbesondere die Behandlung von Differentialgleichungen zu Schwingungsvorgängen vereinfachen, da sich damit die komplizierten Beziehungen in Zusammenhang mit Produkten von Sinus- bzw. Kosinusfunktionen durch Produkte von Exponentialfunktionen ersetzen lassen, wobei lediglich die Exponenten addiert werden müssen. So fügt man dazu beispielsweise in der komplexen Wechselstromrechnung willkürliche aber passende Imaginärteile in die reellen Ausgangsgleichungen ein, die man bei der Auswertung der Rechenergebnisse dann wieder ignoriert. Es handelt sich dabei lediglich um einen Rechentrick ohne philosophischen Hintergrund.
In der Optik werden die brechenden und absorbierenden Effekte einer Substanz in einer komplexen, Wellenlängen-abhängigen Permittivität (Dielektrizitätskonstante) oder der komplexen Brechzahl zusammengefasst, die wiederum auf die elektrische Suszeptibilität zurückgeführt wird.
In der Fluiddynamik werden komplexe Zahlen eingesetzt, um ebene Potentialströmungen zu erklären und zu verstehen. Jede beliebige komplexe Funktion eines komplexen Arguments stellt immer eine ebene Potenzialströmung dar – der geometrische Ort entspricht dem komplexen Argument in der gaußschen Zahlenebene, das Strömungspotenzial dem Realteil der Funktion, und die Stromlinien den Isolinien des Imaginärteils der Funktion mit umgekehrtem Vorzeichen. Das Vektorfeld der Strömungsgeschwindigkeit entspricht der konjugiert komplexen ersten Ableitung der Funktion. Durch das Experimentieren mit verschiedenen Überlagerungen von Parallelströmung, Quellen, Senken, Dipolen und Wirbeln kann man die Umströmung unterschiedlicher Konturen darstellen. Verzerren lassen sich diese Strömungsbilder durch konforme Abbildung – das komplexe Argument wird durch eine Funktion des komplexen Arguments ersetzt. Beispielsweise lässt sich die Umströmung eines Kreiszylinders (Parallelströmung + Dipol + Wirbel) in die Umströmung eines tragflügel-ähnlichen Profils (Joukowski-Profil) verzerren und die Rolle des tragenden Wirbels an einer Flugzeug-Tragfläche studieren. So nützlich diese Methode zum Lernen und Verstehen ist, zur genauen Berechnung reicht sie im Allgemeinen nicht aus.
Komplexe Zahlen in der angewandten Mathematik
Wichtig ist auch die Anwendung komplexer Zahlen bei der Berechnung uneigentlicher reeller Integrale im Rahmen des Residuensatzes der Funktionentheorie.
Komplexe Zahlen in der reinen Mathematik
Die komplexen Zahlen sind der algebraische Abschluss des Körpers der reellen Zahlen. Deshalb treten sie beispielsweise als Eigenwerte reeller Matrizen auf, und dann jeweils zusammen mit dem konjugiert komplexen Eigenwert. Sie ermöglichen auch eine Verbindung zwischen trigonometrischen Funktionen und der Exponentialfunktion, die bei der Fourier-Transformation und den Fourier-Reihen ausgenutzt wird.
Das Studium differenzierbarer Funktionen auf Teilmengen der komplexen Zahlen ist Gegenstand der Funktionentheorie. Sie ist in vieler Hinsicht starrer als die reelle Analysis und lässt weniger Pathologien zu. Beispiele sind die Aussage, dass jede in einem Gebiet differenzierbare Funktion bereits beliebig oft differenzierbar ist, oder der Identitätssatz für holomorphe Funktionen.
Die Funktionentheorie ermöglicht oft auch Rückschlüsse auf rein reelle Aussagen, beispielsweise lassen sich manche Integrale mit dem Residuensatz berechnen. Ein wichtiges Einsatzgebiet dieser Methoden ist die analytische Zahlentheorie, die Aussagen über ganze Zahlen auf Aussagen über komplexe Funktionen zurückführt, häufig in der Form von Dirichletreihen. Ein prominentes Beispiel ist die Verbindung zwischen Primzahlsatz und riemannscher ζ-Funktion. In diesem Zusammenhang spielt die riemannsche Vermutung eine zentrale Rolle.
Die oben erwähnte Starrheit holomorpher Funktionen tritt noch stärker bei globalen Fragen in Erscheinung, d. h. beim Studium komplexer Mannigfaltigkeiten. So gibt es auf einer kompakten komplexen Mannigfaltigkeit keine nichtkonstanten globalen holomorphen Funktionen; Aussagen wie der Einbettungssatz von Whitney sind im Komplexen also falsch. Diese so genannte „analytische Geometrie“ (nicht mit der klassischen analytischen Geometrie von René Descartes zu verwechseln!) ist auch eng mit der algebraischen Geometrie verknüpft, viele Ergebnisse lassen sich übertragen. Die komplexen Zahlen sind auch in einem geeigneten Sinne ausreichend groß, um die Komplexität algebraischer Varietäten über beliebigen Körpern der Charakteristik 0 zu erfassen (Lefschetz-Prinzip).
Komplexe Zahlen in der Elektrotechnik
In der Elektrotechnik besitzt die Darstellung elektrischer Größen mit Hilfe komplexer Zahlen weite Verbreitung. Sie wird bei der Berechnung von zeitlich sinusförmig veränderlichen Größen wie elektrischen und magnetischen Feldern verwendet. Bei der Darstellung einer sinusförmigen Wechselspannung als komplexe Größe und entsprechenden Darstellungen für Widerstände, Kondensatoren und Spulen vereinfachen sich die Berechnungen des elektrischen Stromes, der Wirk- und der Blindleistung in einer Schaltung. Die durch Differentialquotienten oder Integrale gegebene Verkopplung geht über in eine Verkopplung durch trigonometrische Funktionen; die Berechnung der Zusammenhänge lässt sich damit wesentlich erleichtern. Auch das Zusammenwirken mehrerer verschiedener sinusförmiger Spannungen und Ströme, die zu unterschiedlichen Zeitpunkten ihre Nulldurchgänge haben können, lässt sich in komplexer Rechnung leicht darstellen. Genaueres über dieses Thema steht im Artikel über die komplexe Wechselstromrechnung.
In den letzten Jahren hat die digitale Signalverarbeitung außerordentlich an Bedeutung gewonnen, deren Fundament die Rechnung mit komplexen Zahlen bildet.
Siehe auch
Einzelnachweise
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1: Mit Lösungshinweisen zu 420 Übungsaufgaben. 4. Auflage. Springer, Berlin 2007, ISBN 978-3-540-31764-7.
Weblinks
- Schriften, Dokumentationen, Videos
- Wikibooks: Komplexe Zahlen
- Geschichte der komplexen Zahlen
- Eine Facharbeit, die eine Einführung in die komplexen Zahlen gibt
- Rechnen mit komplexen Zahlen
- Dimensions: a math film. Einbettung der komplexen Zahlen in die Darstellung höherer Dimensionen (auch Chaostheorie) insb. Kapitel 5 und 6
- Programme zur direkten Ausführung
Natürliche Zahlen
 | Ganze Zahlen
| Ganze Zahlen  | Rationale Zahlen
| Rationale Zahlen  | Reelle Zahlen
| Reelle Zahlen  | Komplexe Zahlen
| Komplexe Zahlen  | Quaternionen
| Quaternionen  | Oktaven
| Oktaven 
Wikimedia Foundation.

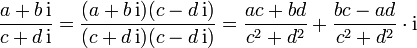
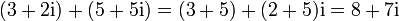
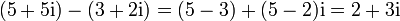
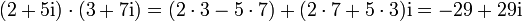
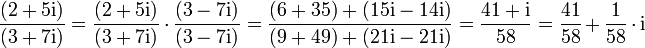
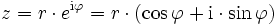
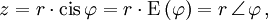

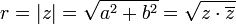

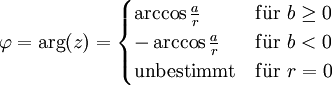

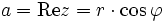
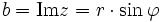
![r\cdot (\cos \varphi + \mathrm{i}\cdot\sin \varphi ) \;\cdot\; s \cdot (\cos \psi + \mathrm{i} \cdot \sin \psi)
= r \cdot s \cdot \left[ \cos (\varphi+\psi) + \mathrm{i} \cdot \sin (\varphi+\psi) \right]](/pictures/dewiki/54/6085dbc5b5bd82187be3ebe8d4232c68.png)
![\frac{r\cdot (\cos \varphi + \mathrm{i} \cdot \sin \varphi)}{s\cdot (\cos \psi + \mathrm{i} \cdot \sin \psi)}
= \frac{r}{s} \cdot \left[ \cos (\varphi-\psi) + \mathrm{i} \cdot \sin (\varphi-\psi) \right]](/pictures/dewiki/54/6e3d460c8d237905944cdef042ab1772.png)

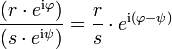
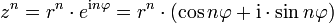
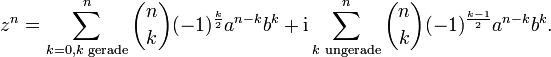

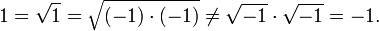
![\sqrt[n]{z} = \sqrt[n]{r}\cdot e^{\mathrm i \frac{\varphi + 2k\pi}n},](/pictures/dewiki/51/35c3d6b701cc5f89be548760d19d21b0.png)