Ist kleiner als

In der Mathematik ist eine Ungleichung eine Aussage über die relative Größe oder Ordnung zweier Objekte.

Die Schreibweise a < b bedeutet a ist kleiner als b und a > b bedeutet a ist größer als b. Weiter bedeutet 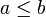$a\le b$, dass a kleiner oder gleich b ist und 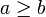$a\ge b$, dass a größer oder gleich b ist.

Wenn die Aussage einer Ungleichung für alle Werte, für die sie definiert ist, die gleiche ist (z. B. n > − 1 für n aus 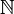$\N$), heißt die Ungleichung absolut oder unbedingt. Gilt die Ungleichung nur für einige Werte der verwendeten Variablen, wird aber für andere Werte umgekehrt oder ist ungültig, so heißt sie bedingt.

Die Richtung einer Ungleichung ändert sich nicht, wenn sie auf beiden Seiten gleich viel verkleinert oder vergrößert wird, oder wenn beide Seiten mit der gleichen positiven Zahl multipliziert oder dividiert werden. Multipliziert oder dividiert man hingegen mit einer negativen Zahl, dreht sich das Ungleichheitszeichen um.

Eigenschaften von Ungleichungen

Trichotomiegesetz

Für zwei reelle Zahlen a und b gilt genau eine der folgenden Beziehungen:

• a < b
• a = b
• a > b

Addition und Subtraktion

Für beliebige reelle Zahlen a,b,c und d gilt:

• Wenn a > b, dann ist a + c > b + c und a − c > b − c.
• Wenn a < b, dann ist a + c < b + c und a − c < b − c.
• Wenn a < b und c < d, dann ist a + c < b + d und a − d < b − c.

Multiplikation und Division

Für beliebige reelle Zahlen a,b und c gilt ($c\ne 0$)

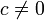• Wenn c positiv ist und a > b, dann ist ac > bc und a / c > b / c
• Wenn c positiv ist und a < b, dann ist ac < bc und a / c < b / c
• Wenn c negativ ist und a > b, dann ist ac < bc und a / c < b / c
• Wenn c negativ ist und a < b, dann ist ac > bc und a / c > b / c

Erweiterung des Begriffes

Der Ungleichungsbegriff wird auch gelegentlich – jedoch nicht einheitlich – z. B. auf komplexe Zahlen, Vektoren oder Matrizen erweitert. Beispiele sind:

• Ist 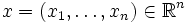$x=(x_1,\ldots,x_n)\in\R^n$, so gilt x > 0 genau dann, wenn x_i > 0 für alle $i\in\{1,\ldots,n\}$.
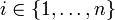  Sind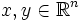 $x,y\in\R^n$, so gilt x > y genau dann, wenn x − y > 0.
  Analog werden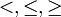 $&amp;lt;,\le,\ge$ definiert.
• Ist 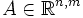$A\in\R^{n,m}$, so gilt A > 0 genau dann, wenn A positiv definit ist.
  Sind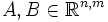 $A,B\in\R^{n,m}$, so gilt A > B genau dann, wenn A − B > 0.
  Ähnlich können auch < oder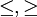 $\le,\ge$ (semidefinit) definiert werden.
• Sei 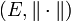$(E,\|\cdot\|)$ ein reeller Banachraum und 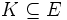$K\subseteq E$ ein Kegel. Sind 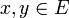$x,y\in E$, so gilt 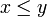$x\le y$ genau dann, wenn $y-x\in K$.

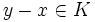Bekannte Ungleichungen

In der Mathematik werden oft Ungleichungen benutzt um Größen, die nicht, oder nur schwer, genau berechnet werden können, einzugrenzen. Folgende Ungleichungen werden sehr häufig benutzt:

• Bernoullische Ungleichung
• Bonferroni-Ungleichungen
• Cauchy-Schwarz-Ungleichung
• Dreiecksungleichung
• Jensensche Ungleichung
• Markow-Ungleichung
• Mittel-Ungleichung

Siehe auch

• Ordnungsrelation, Gleichheit, Lösen von Ungleichungen, Verhältniszeichen, Inversionsgesetz

Literatur

• Godfrey Harold Hardy, John Edensor Littlewood, George Polya: Inequalities. Cambridge University Press, 1952.
• Peter Patzt: Ungleichungstheorie, 2006 (PDF).