- Jacobi-Rotationsverfahren
-
Das Jacobi-Verfahren (nach Carl Gustav Jacob Jacobi (1846)) ist ein iteratives Verfahren zur numerischen Berechnung aller Eigenwerte und -vektoren (kleiner) symmetrischer Matrizen.
Inhaltsverzeichnis
Beschreibung
Da die Ausgangsmatrix
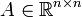 als symmetrisch vorausgesetzt wird, ist sie orthogonal ähnlich zu einer Diagonalmatrix
als symmetrisch vorausgesetzt wird, ist sie orthogonal ähnlich zu einer Diagonalmatrix 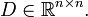
wobei die Diagonale von D die Eigenwerte
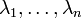 von A enthält und S spaltenweise die zugehörigen Eigenvektoren.
von A enthält und S spaltenweise die zugehörigen Eigenvektoren.
Die Idee des Jacobi-Verfahrens besteht darin, das jeweils betragsgrößte Außerdiagonalelement mit Hilfe einer Givens-Rotation auf 0 zu bringen, und sich auf diese Art mehr und mehr einer Diagonalmatrix anzunähern. Es ergibt sich die Iterationsvorschriftmit
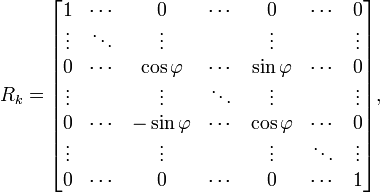
wobei
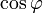 und
und 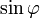 jeweils in der p-ten und q-ten (p < q) Zeile und Spalte stehen und
jeweils in der p-ten und q-ten (p < q) Zeile und Spalte stehen und 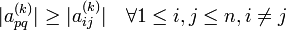 das betragsgrößte Außerdiagonalelement von A(k) darstellt. Die Komponenten von Rk ergeben sich nun aus folgernder Überlegung:
das betragsgrößte Außerdiagonalelement von A(k) darstellt. Die Komponenten von Rk ergeben sich nun aus folgernder Überlegung:Die Transformation
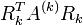 bewirkt speziell in den Kreuzungselementen folgende Veränderungen:
bewirkt speziell in den Kreuzungselementen folgende Veränderungen:- Da
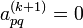 sein soll, ergibt sich aus
sein soll, ergibt sich aus 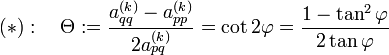
Da die Rotationsmatrizen orthogonal sind und Produkte orthogonaler Matrizen wieder orthogonal sind, wird auf diese Art eine orthogonale Ähnlichkeitstransformation beschrieben. Es lässt sich zeigen, dass die Folge der Matrizen A(k) gegen eine Diagonalmatrix konvergiert. Diese muss aufgrund der Ähnlichkeit dieselben Eigenwerte besitzen.
Klassisches und zyklische Jacobi-Verfahren
Beim klassischen Jacobi-Verfahren wird in jedem Iterationsschritt das betragsmäßig größte Element zu Null gesetzt. Da die Suche nach diesem der Hauptaufwand des Algorithmus ist, wendet das zyklische Jacobi-Verfahren in jedem Iterationsschritt je eine Givensrotation auf jedes Element des strikten oberen Dreiecks an.
Literatur
- Kaspar Nipp, Daniel Stoffer: Lineare Algebra: Eine Einführung für Ingenieure unter besonderer Berücksichtigung numerischer Aspekte. VDF Hochschulverlag AG 2002, ISBN 9783728128188. Abschnitt 10.2 (S. 222-228) (eingeschränkte Online-Version (Google Books))
Weblinks
Wikimedia Foundation.

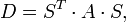

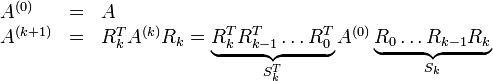
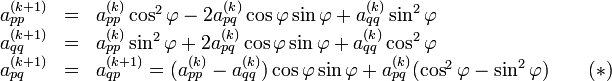
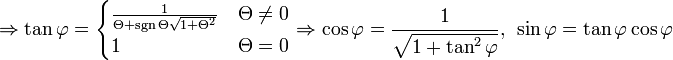
![A^{(k)} \xrightarrow[k\rightarrow\infty]{}\,diag(\lambda_1, \ldots, \lambda_n)](/pictures/dewiki/56/802cd7cf1def36dc0313ba7cf4feedba.png)