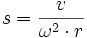Johnston-Ogston-Effekt

Der Sedimentationskoeffizient ist der Quotient aus der maximalen Sedimentationsgeschwindigkeit eines Teilchens in einer Zentrifuge geteilt durch die Stärke des Zentrifugalfelds. Die Dimension des Koeffizienten ist Zeit, seine Maßeinheit ist Svedberg, abgekürzt S, entsprechend 10⁻¹³ s. Benannt ist die Maßeinheit nach dem schwedischen Chemiker Theodor Svedberg.

Definition

Die Größe des Sedimentationskoeffizienten hängt ab von der Masse und Form des Teilchens sowie seiner Wechselwirkung mit dem Medium, in dem das Teilchen sedimentiert. Er kann deshalb bei Verwendung eines Mediums mit bekannten Eigenschaften zur Bestimmung der Beschaffenheit des Teilchens, insbesondere seiner Masse, verwendet werden. Hauptsächlich werden so in der Biologie mittels einer Zentrifuge die Massen sehr kleiner Teilchen bestimmt, zum Beispiel Ribosomen, Virionen, Proteinmoleküle. Um bei derartig kleinen Teilchen ein ausreichendes Zentrifugalfeld zu erhalten, werden in der Regel Ultrazentrifugen verwendet.

Beim Zentrifugieren entsteht ein Zentrifugalfeld, dessen Stärke bei einer Winkelgeschwindigkeit ω (= 2π · Umdrehungsfrequenz) im Abstand r von der Rotationsachse ω²·r beträgt. Auf ein Teilchen wirkt in diesem Abstand eine Zentrifugalkraft, die gleich dem Produkt der effektiven Masse des Teilchens m_e und der Stärke des Zentrifugalfelds ist, also gleich m_e·ω²·r. Hier ist die effektive Masse m_e maßgeblich, die wegen des Auftriebs des Teilchens im Medium geringer ist als die tatsächliche Masse m. Zwischen der tatsächlichen Masse m und der effektiven Masse m_e besteht die Beziehung m_e = m(1 – V·ρ), worin V das partielle spezifische Volumen des Teilchens und ρ die Dichte des Mediums ist.

Die Zentrifugalkraft beschleunigt das Teilchen radial nach außen. Mit zunehmender Geschwindigkeit des Teilchens steigt die Reibung zwischen dem sedimentierenden Teilchen und dem umgebenden Medium an. Der Reibungswiderstand f·v ist proportional zur Sedimentationsgeschwindigkeit v, der Proportionalitätsfaktor f ist der Reibungskoeffizient des Teilchens in diesem Medium, der von der Form, der Größe und der Hydratation des Teilchens sowie von der Viskosität des Mediums abhängt. Die Sedimentation des Teilchens wird so lange beschleunigt, bis der Reibungswiderstand gleich der Zentrifugalkraft ist, sie also kompensiert, bis also v·f = m_e·ω²·r ist. Von da an sedimentiert das Teilchen mit gleichbleibender Geschwindigkeit v. Dividiert man diese Sedimentationsgeschwindigkeit v durch die Stärke des Zentrifugalfelds ω²·r, so erhält man eine Größe, die nur noch von der Beschaffenheit des Teilchens und seinem Reibungskoeffizienten in dem betreffenden Medium abhängig ist, mit der also bei bekannter Wechselwirkung mit dem umgebenden Medium die Beschaffenheit (u. a. Masse) des Teilchens bestimmt werden kann. Diese Größe wird als Sedimentationskoeffizient s bezeichnet.

$s=\frac {v}{\omega^2 \cdot r}$

Seine Dimension ergibt sich aus $[s] = \frac{\frac{\mathrm{L\ddot{a}nge}}{\mathrm{Zeit}}}{\frac{1}{\mathrm{Zeit}^2} \cdot \mathrm{L\ddot{a}nge}} = \frac{\mathrm{L\ddot{a}nge} \cdot \mathrm{Zeit}^2}{\mathrm{Zeit} \cdot \mathrm{L\ddot{a}nge}} = \mathrm{Zeit}$

Bei der Bestimmung der Masse von Teilchen aus ihrem Sedimentationskoeffizienten ist zu berücksichtigen, dass zwei Teilchen gleicher Masse unterschiedliche Sedimentationskoeffizienten haben können, wenn sie unterschiedliche Dichten (Einfluss auf den Auftrieb) und Formen (Einfluss auf den Reibungskoeffizient) haben. Deshalb können auch bei Zusammenlagerung zweier Teilchen deren Sedimentationskoeffizienten nicht einfach addiert werden. Zum Beispiel hat ein komplexes Ribosom aus zwei ribosomalen Untereinheiten von 30 S und 50 S keinen Sedimentationskoeffizienten von 80 S, sondern von „nur“ 70 S.

Ist der Sedimentationskoeffizient zweier Stoffe jeweils von der Konzentration des anderen Stoffes abhängig, ist zu beobachten, dass der langsamer sedimentierende Stoff relativ zum schnelleren höher konzentriert ist, als erwartet. Dies nennt man Johnston-Ogston-Effekt, der nach den Biochemikern Joseph Johnston und Alexander Ogston benannt ist.

Weblinks

• Arbeitsmethoden der Biochemie, von Alfred Pingoud, Alfred Pingoud, Claus Urbanke (als Google-Book)