Jonkheere-Terpstra-Test

Der Jonkheere-Terpstra-Test ist ein parameterfreier statistischer Test, mit dem ähnlich wie beim Kruskal-Wallis-Test im Rahmen einer Varianzanalyse verglichen wird, ob sich verschiedene unabhängige Stichproben (Gruppen) hinsichtlich einer ordinalskalierten Variable unterscheiden. Der Unterschied zum Kruskal-Wallis-Test ist, dass hier auf das Vorliegen eines Trends zwischen den Gruppen getestet wird.

Die Nullhypothese H₀ lautet für die Erwartungswerte G der Gruppen: $G_1\ =\ G_2\ = \ \dots\ = \ G_c$

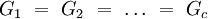
Als Alternativhypothese H_A gilt: 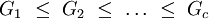$G_1\ \leq\ G_2\ \leq\ \dots\ \leq\ G_c$, wobei mindestens eine strikte Ungleichung gilt.

Berechnung

Die Teststatistik J lautet für eine Anzahl c von Gruppen mit jeweils n Messungen:

$J\ = \ \sum_{i<j}^c U_{ij} \ = \ \sum_{i=1}^{c-1}\ \sum_{j=i+1}^{c}U_{ij}$

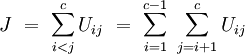
Dabei ist U_ij definiert als

$U_{ij}\ = \ \sum_{s=1}^{n_i}\ \sum_{t=1}^{n_j}\Psi (X_{jt}\ -\ X_{is})$

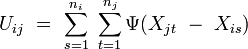
mit

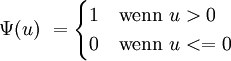$\Psi (u)\ = \begin{cases} 1 & \text{wenn } u > 0 \\ 0 & \text{wenn } u <= 0 \end{cases}\$ oder im Falle von Bindungen (gleichen Messwerten)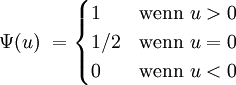 $\ \Psi (u)\ = \begin{cases} 1 & \text{wenn } u > 0 \\ 1/2 & \text{wenn } u = 0 \\ 0 & \text{wenn } u < 0 \end{cases}$

Die berechnete Prüfgröße J wird größer, wenn ein Trend zwischen den Gruppen vorhanden ist.

Unter allgemeinen Bedingungen weist die Prüfgröße J eine Normalverteilung auf. Für den Erwartungswert μ_J und dessen Varianz σ_J gelten folgende Formeln:

$\mu _J\ = \ \frac{N^2\ - \ \sum_{i=1}^{c}n_i^2}{4}\$

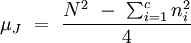
und

$\ \sigma _J\ = \ \sqrt{\frac{N^2(2N + 3)\ - \ \sum_{i=1}^{c}n_i^2(2n_i+3)}{72}}$

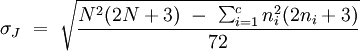
Die daraus folgende Variable Z ist standardnormalverteilt, wenn die Gesamtzahl aller Stichproben größer 12 ist:

$Z\ = \ \frac{J\ - \ \mu _J}{\sigma _J}$

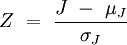
Oder anders ausgedrückt: bei einem einseitigen Test auf 5% Niveau (Irrtumswahrscheinlichkeit) ist der Test signifikant, wenn

$J\ >\ \mu _J\ +\ 1,645\sigma _J$

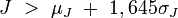
Verallgemeinerung

Es lassen sich neben einem monotonen Trend auch Modelle bearbeiten, bei denen ein anfänglicher Aufwärtstrend an einem bestimmten Punkt in einen Abwärtstrend übergeht. Dieses ist dann die Verallgemeinerung des Jonkheere-Terpsta-Tests, der Umbrella-Test nach Mack und Wolfe.^[1]

Literatur

1. ↑ H. B. Mack: K-sample rank tests for umbrella alternatives. In: J. Amer. Statist. Ass.. 76, 1981, S. 175-81

• A. R. Jonckheere: A distribution-free k-sample test against ordered alternatives. In: Biometrica. 41, 1954, S. 133-45
• A. R. Jonckheere: A test of significance for the relation between m rankings and k ranked categories. In: British Journal of Statistical Psychology. 7, 1954, S. 93-100
• T. J. Terpstra: The asymptotic normality and consistency of Kendall's test against trend, when ties are present in one ranking. In: Indagationes Mathematicae. 14, 1952, S. 327-33
• W.J. Conover: Practical Nonparametric Statistics, 3, S. 5.4, New York: John Wiley & Sons, Inc. 1999, ISBN 0-471-16068-7