Analog-zu-Digital-Umsetzer

Ein Analog-Digital-Umsetzer ADU, englisch ADC für Analog-to-Digital-Converter (auch Analog-Digital-Wandler oder A/D-Wandler) setzt nach unterschiedlichen Methoden analoge Eingangssignale in digitale Daten bzw. einen Datenstrom um, die dann weiterverarbeitet oder gespeichert werden können. Das Gegenstück ist der Digital-Analog-Umsetzer oder DAU.

Funktion

Spektrum eines bandbegrenzten Signals (blau) und dessen hypothetische Spiegelfrequenzen (grün) ohne Überlappung, also korrekter Abtastung.

Der ADU quantisiert ein kontinuierliches Spannungssignal sowohl in der Zeit als auch in der Amplitude. Jedes Signal stellt sich dadurch nach der Umsetzung in einem Amplituden-Zeit Diagramm (Oszilloskop) treppenförmig dar. Die Hauptparameter eines ADUs sind seine Auflösung in Bit und seine Umsetzungsgeschwindigkeit, wovon die maximale Umsetzungsrate abhängt. Die Auflösung ist gleichzeitig die Genauigkeitsgrenze für die Umsetzung. Die nutzbare Genauigkeit wird durch Nichtlinearitäten im analogen Schaltungsteil des ADUs verringert. Die Umsetzungsgeschwindigkeit ist meistens konstant, kann aber bei speziellen Umsetzertypen vom Wert der anliegenden Spannung abhängen.

Zeitliche Quantisierung und Aliasing

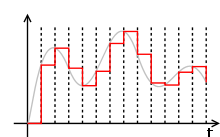
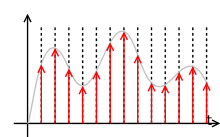Zeitliche Quantisierung durch Sample-and-Hold-Schaltung, wertmäßig kontinuierlich

Jeder A/D-Umsetzer braucht zur Konvertierung Zeit. Je kürzer diese ist, desto höher kann die Umsetzgeschwindigkeit oder Abtastfrequenz sein. Die Wahl einer geeigneten Abtastfrequenz hängt jedoch auch vom erwarteten Eingangssignal ab.

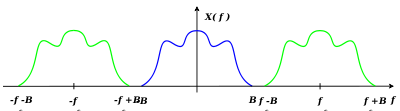
Um das Signal später richtig rekonstruieren zu können (Alias-Effekt), muss die Abtastfrequenz mindestens das Doppelte der maximal möglichen Eingangsfrequenz betragen (Nyquist-Frequenz). Manchmal ist das abzutastende Signal allerdings so hochfrequent, dass man diese Bedingung technisch nicht realisieren kann. In diesem Fall kommt es zu einer Unterabtastung, die zunächst einmal keine korrekte Rekonstruktion mehr erlaubt (vergl. Nyquist-Shannon-Abtasttheorem). Wenn das Eingangssignal jedoch stationär ist, kann man durch Mehrfachabtastung mit zeitlichem Versatz dennoch eine Rekonstruktion ermöglichen, ohne dabei das Abtasttheorem zu verletzen.

Im Idealfall findet die A/D-Umsetzung in immer exakt gleichen Zeitabständen statt. In der Realität ist diese Bedingung schwierig zu erreichen. Durch kleine Variationen der Abstände tritt ein Effekt auf, den man als Jitter bezeichnet. Auch ein Jitter beeinträchtigt die spätere Rekonstruktion des Ursprungssignals.

In der späteren Rekonstruktion des Ursprungssignals treten außerdem Artefakte auf, die durch die Abtastung selbst entstehen und die in der Regel unerwünscht sind. Um sie zu entfernen, setzt man in der Regel einen Tiefpass-Filter (Anti-Aliasing-Filter) ein, der die unerwünschten Frequenzbereiche unterdrückt. Mit zunehmender Überabtastung (mit mehr als der doppelten Signalfrequenz) wird dieser Filter einfacher zu konstruieren.

Während der Signalumsetzung darf sich das Eingangssignal idealerweise nicht ändern. In der Regel schaltet man dem eigentlichen A/D-Umsetzer deshalb eine Sample-and-Hold-Schaltung (engl. Sample and hold circuit) vor, die den Signalwert analog so zwischenspeichert, dass er während der Digitalisierung konstant ist. Dies trifft besonders auf die stufen- und bitweisen Umsetzer zu, die längere Konvertierungszeiten benötigen. Integrierte Umsetzer enthalten heute meist eine Abtast-Halte-Schaltung, falls diese notwendig ist.

Wertmäßige Quantisierung

Zeit- und wertmäßig quantisiertes Signal wie am Ausgang eines A/D-Umsetzers

Die Quantisierung in eine endliche Anzahl von Quantierungsstufen, die praktisch immer in Bits vorgenommen wird, hat eine reduzierte Auflösung und Quantisierungsfehler zur Folge. Bei Wechselspannung werden diese Fehler als Fehler-Wechselspannungen betrachtet, die Quantisierungsrauschen genannt werden und bei einem idealen Analog-Digital-Umsetzer einen Rauschabstand von etwa 6 dB pro Bit ermöglichen. Selbstverständlich unterliegt auch ein ADU dem analogen Rauschen.

Quantisierungskennlinie

Bei einem idealen Analog-Digital-Umsetzer besteht ein offset-freier, linearer Zusammenhang zwischen Eingangs- und Ausgangsgröße. Es gibt auch A/D-Umsetzer mit nichtlinearer Quantisierungskennlinie z. B. nach dem logarithmischen A-law- und µ-law-Verfahren für Telefonnetze, die aber aus binären Werten abgeleitet werden.

Bezugswert

Da das dem ADU zugeführte Analogsignal in einen größenlosen Digitalwert umgesetzt wird, muss es mit einem vorgegebenen elektrischen Wert oder Signal bewertet werden (Eingangsspannungsbereich). Im allgemeinen wird ein feststehender Bezugswert (z. B. intern erzeugte Referenzspannung) verwendet. Das analoge Eingangssignal wird digital abgebildet, die Referenz legt die maximale Amplitude des Eingangssignals fest.

Grundsätzlich ist mit einer Variation des Bezugswertes eine 2-Quadranten-Multiplikation oder Modulation möglich, wobei im Gegensatz zu D/A-Umsetzern der Bereich der Referenzspannung nur in einem geringeren Umfang variieren kann.

Genauigkeit

Nichtlinearität und Amplitudenfehler

Durch den Vergleich der Kennlinien von idealem und realem Umsetzer sind folgende Fehler definiert (siehe Abb. 3):

• Verstärkungsfehler (engl. Gain-Error)
• Nullpunktfehler (Offset)
• Nichtlinearität

Der amplitudenmäßige Fehler wird auch oft in Bruchteilen des LSB angegeben. Für eine nicht monotone Kennlinie gilt, dass es innerhalb des Kurvenverlaufes Intervalle gibt, für die U_aus(n) < U_aus(n − 1) gilt. Als Gesamtwert aller Ungenauigkeiten wird gerade für Wechselspannungen auch oft die effektive Anzahl von Bits als Rechenwert des Rauschabstands angegeben.

Zeitliche und Apertur-Fehler

Bei der Digitalisierung einer Sinusspannung 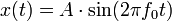$x(t)=A\cdot\sin (2 \pi f_0 t)$ entsteht durch zeitliche Schwankungen des Taktes Δt (clock jitter) sowie Varianz der Schaltung ein der Eingangsfrequenz proportionaler Fehler 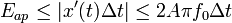$E_{ap} \le |x'(t) \Delta t| \le 2A \pi f_0 \Delta t$. Der maximal erlaubte Jitter bei einer Auflösung q des ADU kann berechnet werden zu: $\Delta t &amp;amp;lt; \frac{1}{2^q \pi f_0}$.

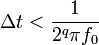ADU- Auflösung in Bit	Eingangsfrequenz
	1 Hz	44,1 kHz	192 kHz	1 MHz	10 MHz	100 MHz	1 GHz
8	1243 µs	28,2 ns	6,48 ns	1,24 ns	124 ps	12,4 ps	1,24 ps
10	311 µs	7,05 ns	1,62 ns	311 ps	31,1 ps	3,11 ps	0,31 ps
12	77,7 µs	1,76 ns	405 ps	77,7 ps	7,77 ps	0,78 ps	0,08 ps
14	19,4 µs	441 ps	101 ps	19,4 ps	1,94 ps	0,19 ps	0,02 ps
16	4,86 µs	110 ps	25,3 ps	4,86 ps	0,49 ps	0,05 ps	–
18	1,21 µs	27,5 ps	6,32 ps	1,21 ps	0,12 ps	–	–
20	304 ns	6,88 ps	1,58 ps	0,16 ps	–	–	–
24	19,0 ns	0,43 ps	0,10 ps	–	–	–	–
32	74,1 ps	–	–	–	–	–	–

Realisierungsverfahren

Es gibt eine große Anzahl von Verfahren, die zur Umsetzung von analogen in digitale Signale benutzt werden können. Im Folgenden sind die wichtigsten Prinzipien aufgeführt:

Stufenweise Umsetzer (Zählverfahren)

---

Beim Zählverfahren wird so lange der kleinste gewünschte Schritt (LSB) aufeinander addiert und an einen Komparator geliefert, bis der Wert gleich oder größer der angelegten analogen Referenzgröße ist. Die Schritte werden mit einem Zähler erzeugt, der dem Verfahren seinen Namen gibt. Der Schaltungsaufwand ist sehr gering, allerdings ist die Umsetzungszeit abhängig von der Eingangsgröße, im ungünstigsten Fall muss der Zähler alle Stufen durchlaufen. Verbesserte Varianten des Zählverfahrens sind der:

Single-Slope-Umsetzer (Sägezahn-/Einrampenverfahren/Zählverfahren)

Funktionsprinzip eines ADUs nach dem Sägezahnverfahren

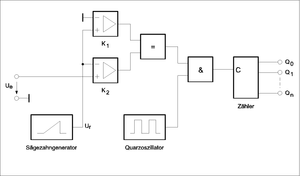
Beim Sägezahnverfahren wird die Ausgangsspannung U_r eines Sägezahngenerators über zwei Komparatoren K₁ und K₂ mit dem Massepotential (0 V) und mit der ADU-Eingangsspannung U_e verglichen. Während des Zeitraums, in dem die Sägezahnspannung den Bereich zwischen 0 V und der Spannung U_e durchläuft, werden die Pulse eines Quarzoszillators durch einen Zähler summiert. Aufgrund der konstanten Steigung der Sägezahnspannung ist die verstrichene Zeit und somit der Zählerstand bei Erreichen von U_r = U_e proportional zur Höhe der ADU-Eingangsspannung. Nach dem Ende des Zählvorgangs wird das Zählergebnis in ein Register übertragen und steht als digitales Signal zur Verfügung. Anschließend wird der Zähler zurückgesetzt und ein neuer Umsetzungsvorgang beginnt.

Die Umsetzungszeit bei diesem ADU ist abhängig von der Eingangsspannung. Zeitlich schnell veränderliche Signale können mit diesem Umsetzertyp nicht korrekt umgesetzt werden. Umsetzer nach dem Sägezahnverfahren sind sehr ungenau, da der Sägezahngenerator mit Hilfe eines temperatur- und alterungsabhängigen Integrationskondensators arbeitet. Sie werden wegen ihres relativ geringen Schaltungsaufwandes für einfache Aufgaben eingesetzt, z. B. in Spielkonsolen, um die Stellung eines Potentiometers, das durch einen Joystick oder ein Lenkrad bewegt wird, zu digitalisieren.

Dual-, Quad- und Multislope-Umsetzer (Mehrrampenverfahren)

Dual-, Quad- und Multislope-Umsetzer sind eine Weiterentwicklungen der Einrampen-Umsetzer und bestehen im Wesentlichen aus einem Integrator und mehreren elektronischen Schaltern. Der Integrator arbeitet mit einem externen, hochwertigen Kondensator, der in zwei oder mehr Zyklen geladen und entladen wird. Zunächst wird der Integratoreingang mit der unbekannten ADU-Eingangsspannung verbunden und es erfolgt die Ladung über ein fest vorgegebenes Zeitintervall. Für die anschließende Entladung wird der Integrator mit einer bekannten Referenzspannung entgegengesetzter Polarität verbunden. Die benötigte Entladezeit bis zum Erreichen von null am Integratorausgang wird durch einen Zähler ermittelt und daraus die unbekannte Eingangsspannung bestimmt. Zur Kompensation von internen Offsetfehlern des ADU wird beim Vierrampenverfahren noch ein weiterer Lade-/Entladezyklus bei kurzgeschlossenem Integratoreingang durchgeführt. Die Referenzspannung muss immer konstant gehalten werden, d. h. beispielsweise, dass thermisch bedingte Schwankungen vermieden werden müssen.

Derartige Umsetzer nach dem Mehrrampenverfahren sind relativ langsam (hohe Konversionsdauer), benötigen keine Abtast-Halte-Schaltung und bieten eine sehr hohe Auflösung sowie gute differentielle Linearität und gute Unterdrückung von Störsignalen wie Rauschen, Netzeinkopplung. Das typische Einsatzgebiet sind Digitalmultimeter, da sich bei geeigneter Integrationsdauer überlagerte 50-Hz-Störungen der Netzfrequenz eliminieren lassen.

Delta-Sigma-Verfahren

Das Delta-Sigma-Verfahren, auch als Charge-Balance-Verfahren oder als 1-Bit-Umsetzer bezeichnet, basiert auf der Delta-Sigma-Modulation. Ein Eingangssignal kommt über einen analogen Subtrahierer zum Integrator und verursacht an dessen Ausgang ein Signal, das von einem Komparator mit Eins oder Null bewertet wird. Dieser Komperator, gleichwertig zu einem 1-Bit-Digital-Analog-Umsetzer, erzeugt daraus eine positive oder negative Spannung, die über den Subtrahierer den Integrator wieder auf Null zurückzieht (Regelkreis). Der nachgeschaltete Digitalfilter setzt den seriellen und hochfrequenten Bit-Strom in digitale also diskrete Werte um, die den Analogwert am Eingang mit niedrigerer Erneuerungsrate aber hoher Auflösung wiedergeben. Das Ergebnis kann parallel oder seriell ausgegeben werden.

Der Vorteil des Delta-Sigma Umsetzers im Vergleich zum einfachen Zählverfahren ist, dass die Dynamik in gewissen Grenzen durch die Bandbreite wechselseitig ausgetauscht werden kann und so eine Rauschformung mit größeren Signal-Rausch-Verhältnis erzielbar ist. Eine geringe Dynamik von nur einem Bit (Komperator) in der Eingangsstufe erfordert eine hohe Überabtastung um bei niedriger Abtastrate eine hohe Dynamik von 20 bis 24 Bit pro Abtastwert zu erzielen. In Praxis werden Delta-Sigma-Umsetzer als Systeme höherer Ordnungen aufgebaut, d. h. durch mehrere seriell angeordnete Differenz- und Integratorstufen. Eine hohe Überabtastung vereinfacht bzw. reduziert die Ordnung des analogen Anti-Aliasing-Filters.

Der Vorteil des größeren Signal-Rausch-Verhältnis wird durch den Nachteil der vergleichsweise hohe Latenz erkauft, welche vor allem durch die Filterstufen bedingt ist. Delta-Sigma Umsetzer werden daher dort eingesetzt, wo kontinuierliche Signalverläufe und nur moderate Bandbreiten benötigt werden, wie beispielsweise im Audiobereich. Praktisch alle Audiogeräte im Bereich der Unterhaltungselektronik wie zum Beispiel Compact Disc-Spieler, SACD oder DAT-Rekorder setzten diese Wandler ein.

Auch bei Datenumsetzern in der Kommunikationstechnik und der Messtechnik wird es aufgrund der fallenden Preise zunehmend eingesetzt. Durch die bei diesem Verfahren notwendige hohe Überabtastung sind dem Verfahren bei höheren Frequenzen von einigen MHz aufwärts allerdings Grenzen gesetzt.

Tracking-Umsetzer

Diese ähneln den Slope-Umsetzern, nur werden die Rampen mittels eines Auf-/Abwärtszählers und eines nachgeschalteten DACs anstelle eines Integrators erzeugt. Oft sind die Rampen derartiger Umsetzer simpel und monoton; sie „fahren“ dem Signal einfach nach, woraus sich erklärt, dass die Umsetzungszeit derartiger ADCs vom Abstand des aktuellen Eingangssignals zum letzten gemessenen Zustand des Eingangssignals abhängt.

Bitweise Umsetzer: Sukzessive Approximation

---

Prinzipskizze eines ADUs nach dem Verfahren der sukzessiven Approximation

Kennzeichnend ist die Annäherung eines Vergleichswertes an den analogen Ausgangswert. Einfache sukzessive Approximation setzt dabei pro Schritt ein binäres Bit um. Um Größenordnungen genaueres und schnelleres Umsetzen kann erreicht werden, indem die Umsetzung redundant erfolgt, also pro Schritt nur ein Teil eines Bits umgesetzt wird.

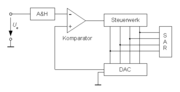
Ein ADU, der nach dem Verfahren der sukzessiven Approximation (d. h. schrittweise Annäherung) arbeitet, grenzt das eingehende Signal mittels Intervallschachtelung ein. Dazu besitzt er im einfachsten Fall ein Datenregister (successive approximation register, SAR), in dem zum Schluss der ermittelte digitale Wert steht, einen Digital-Analog-Umsetzer, der eine dem momentanen Digitalwert des Datenregisters entsprechende analoge Referenzspannung erzeugt, einen Komparator, der die erzeugte Referenzspannung mit der Eingangsspannung vergleicht, und ein Steuerwerk. Für jedes Bit an Genauigkeit benötigt ein einfacher ADU jeweils einen Taktzyklus Umsetzungszeit. Derartige Umsetzer erreichen Auflösungen von 16 Bit bei einer Umsetzungsrate von 1 MHz.

Wägeverfahren

Ein mögliches Approximationsverfahren ist das Wägeverfahren. Dabei werden zunächst alle Bits auf Null gesetzt. Beginnend beim Most Significant Bit (MSB) werden abwärts bis zum Least Significant Bit (LSB) nacheinander alle Bits des Digitalwerts ermittelt.
In jedem Taktzyklus wird vom Steuerwerk jeweils das in Arbeit befindliche Bit probeweise gesetzt; der Digital-Analog-Umsetzer erzeugt die dem aktuellen Digitalwert entsprechende Referenzspannung. Der Komparator vergleicht die Referenzspannung mit der Eingangsspannung U_e und veranlasst das Steuerwerk, das in Arbeit befindliche Bit wieder zurückzusetzen, wenn die Referenzspannung höher ist als die Eingangsspannung. Wenn die Referenzspannung kleiner oder gleich der Eingangsspannung ist, bleibt das Bit gesetzt. So erfolgt schrittweise eine (sukzessive) Annäherung der Referenzspannung an die Eingangsspannung. Während der Umsetzung darf sich das Eingangssignal U_e nicht ändern, da sonst die niederwertigen Bits auf Grundlage einer anderen Eingangsspannung gewogen werden würden. Deshalb ist dem Eingang eine Abtast-Halte-Schaltung vorgeschaltet. Bei schnellen Konvertern ist das Approximationsverfahren inklusive Abtast-Halte-Schaltung als Pipeline ausgeführt.

Redundante Umsetzer

Dem Wägeverfahren ähnliche redundante Analog-Digital-Umsetzer gehen davon aus, dass keine exakte Halbierung des noch offenen Intervalls um den Zielwert herum erfolgt, sondern dieses Intervall nur um einen Anteil davon eingeschränkt wird. Dazu haben sie einen Digital-Analog-Umsetzer, dessen Elemente nicht nach dem Dualsystem gestaffelt sind, also immer um den Faktor 2, sondern nach einem kleineren Faktor. Sie nehmen damit einerseits in Kauf, dass mehr Elemente benötigt werden, um den gleichen Wertebereich abzudecken, ermöglichen aber andererseits, dass der Umsetzer um eine Größenordnung schneller arbeiten und eine um mehrere Größenordnungen höhere Genauigkeit erzielen kann: Die schnellere Funktion kommt dadurch, dass der Komparator in jedem Schritt nicht abwarten muss, bis sich seine Verstärker bis zu einem Mehrfachen der Zielgenauigkeit eingeschwungen haben (immer etwas größenordnungsmäßig soviele Einschwing-Zeitkonstanten, wie der Umsetzer Bits umsetzen soll), sondern eine Entscheidung schon nach unglaublich kurzen 1-2 Einschwing-Zeitkonstanten abgeben kann, die dann in einem recht großen Bereich innerhalb des Restintervalls fehlerhaft ist. Das wird allerdings mehr als abgefangen durch die redundant ausgelegten Umsetzerelemente. Die Gesamtgeschwindigkeit eines solchen Umsetzers liegt größenordnungsmäßig eine Zehnerpotenz über der seines einfachen Vorbilds. Durch den redundanten Umsetzungsprozess hat ein solcher Umsetzer ein viel geringeres Eigenrauschen als sein rein dualer Gegenpart. Zusätzlich kann sich ein solcher ADU selbst einmessen, und zwar bis zu einer Genauigkeit, die nur durch das Rauschen begrenzt ist. Indem man das Selbsteinmessen wesentlich langsamer ablaufen lässt als die Umsetzung in der Nutzanwendung, kann das Rauschen in diesem Prozess um eine Größenordnung gedrückt werden. Die resultierende Kennlinie eines solchen Umsetzers ist bis auf eine rauschartige Abweichung um wenige Vielfache des kleinsten beim Selbsteinmessen verwendeten Elements absolut linear. Indem zwei derartige Umsetzer nebeneinander auf denselben Chip platziert werden und einer immer im Einmess-Modus ist, können solche Umsetzer nahezu absolut resistent gegen Herstellungstoleranzen, Temperatur- und Betriebsspannungsänderungen gemacht werden. Die erreichbare Auflösung ist ausschließlich rauschbegrenzt. Das Rauschen liegt je nach konkreter Ausführung etwa um 10 dB über dem Temperaturrauschen. Die erreichbare Geschwindigkeit gleichzeitig bei einigen 100 MHz.

Eine weitere Verallgemeinerung des Approximationsverfahrens sind Pipeline-Umsetzer, die sich dem Zielwert pro Approximationsschritt um mehrere Bits annähern.

Flash-Umsetzer (Parallel-Umsetzer)

---

Die direkte Methode oder auch Flash-Umsetzung basiert (ähnlich wie sukzessiv approximierende Umsetzer) auf Vergleichern (Komparatoren). Kennzeichnend ist die Umsetzung eines gesamten Ausgangswertes gleichzeitig. Allerdings ist bei Flash-Umsetzern für jeden möglichen Ausgangswert (bis auf den kleinsten bzw. größten) ein separat implementierter Komparator erforderlich. Ein 8-Bit-Flash-Umsetzer benötigt somit z. B. 2⁸−1 = 255 Komparatoren. Bei höheren Auflösungen steigt der erforderliche Aufwand drastisch an, weshalb Flash-Umsetzer typischerweise nur in kleinen Auflösungen von etwa 4 bis 12 Bit verfügbar sind.

Das analoge Eingangssignal wird im Flash-Umsetzer gleichzeitig von allen Komparatoren mit den (über einen mehrstufigen Spannungsteiler erzeugten) Referenzgrößen verglichen. Anschließend erfolgt durch eine Kodierlogik die Umsetzung der 2ⁿ−1 Komparatorsignale in einen n bit breiten Binärcode (mit n: Auflösung in bit). Das Resultat steht damit nach den Durchlaufverzögerungen (Schaltzeit der Komparatoren sowie Verzögerung der Kodierlogik) sofort zur Verfügung.

Flash-Umsetzer kommen normalerweise in allen Digitaloszilloskopen und bei der Digitalisierung von Videosignalen zur Anwendung. Als Beispiel ermöglicht der MAX108 bei einer Auflösung von 8 bit eine Abtastrate von 1,5 GHz. Bei heutigen Digitaloszilloskopen mit möglichen Abtastraten von 20 Gigasample je Sekunde werden zusätzlich noch Demultiplexer vorgeschaltet.

Pipeline-Umsetzer

---

Pipeline-Umsetzer sind mehrstufige Analog-Digital-Umsetzer, die mehrere selbständige interne Stufen besitzen und in Pipeline-Architektur aufgebaut sind. Sie funktionieren äquivalent den bitweisen Approximations-Umsetzern, sind aber eine Verallgemeinerung des Verfahrens, da pro Approximationsschritt eine Annäherung an den Zielwert um mehrere Bits erfolgt.

Ihre Stufen bestehen in der Regel aus Flash-Umsetzern. In jeder Pipelinestufe wird eine grobe Quantisierung vorgenommen, dieser Wert wieder in ein Signal umgesetzt und von dem Eingangssignal abgezogen. Der Restwert wird an die nächste Stufe weitergeleitet. Der Vorteil ist eine höhere Geschwindigkeit. Diese mehrstufigen Umsetzer erreichen Datenraten von mehr als 150 MSPS bei einer Auflösung von 14 Bit.

Die Werte der Quantisierungsstufen werden unter Berücksichtigung ihrer Gewichtung addiert. Meistens enthält ein Korrektur-ROM noch Kalibrierungsdaten, die dazu dienen, Fehler zu korrigieren, die in den einzelnen Digitalisierungsstufen entstehen. Bei manchen Ausführungen werden diese Korrekturdaten auch auf ein externes Signal hin generiert und in einem Random Access Memory abgelegt. Diese Umsetzer erreichen Auflösungen von 14 Bit bei einer Datenausgangsrate von 5 MHz.

Hybrid-Umsetzer

---

Ein Hybrid-Umsetzer ist kein eigenständiger Umsetzer sondern kombiniert zwei oder mehr Umsetzungsverfahren. Zum Beispiel auf Basis einer SAR-Struktur, wobei der ursprüngliche Komparator durch einen Flash-Umsetzer ersetzt wird. Dadurch kann in jedem Approximationsschritt mehr als ein Bit ermittelt werden.

Wichtige Kenngrößen

• Umsetzgeschwindigkeit (Conversion Speed) – Die Dauer einer Umsetzung (Konversionsdauer).
• Auflösung (Resolution) – Die Anzahl der Bits, die zur Darstellung des Eingangssignals verwendet werden. Dieses bestimmt den Quantisierungsfehler. Für die Beurteilung der Genauigkeit des Analog-Digital-Umsetzers ist aber die Auflösung nur ein erster Anhaltspunkt, da weitere Fehlerquellen hinzukommen.
• Effektive Anzahl von Bits (ENOB, Effective Number of Bits). Die tatsächliche Auflösung bei Berücksichtigung aller Fehlerquellen.
• Latenzzeit – Jeder A-D- oder D-A-Umsetzer benötigt zur Umsetzung eine gewisse Zeit. Bei vielen Anwendungen soll diese möglichst klein sein bzw. darf eine gewisse Grenze nicht überschreiten.
• Linearitätsfehler – Die Kennlinie weicht von der idealen Kennlinie ab.
• Nullpunktsfehler – Die Umsetzerkennlinie ist seitlich verschoben.
• Verstärkungsfehler – Der digitale Wert unterscheidet sich um einen konstanten Prozentsatz von der Eingangsspannung. Die mittlere Steigung der Umsetzerkennlinie weicht von 1 ab.
• Integrale Nichtlinearität – Der Fehler zwischen dem umgesetzten Wert und dem eigentlichen Wert. (Höhe)
• Differentielle Nichtlinearität – Abweichung der Breite der Umsetzungsintervalle vom Idealwert
• Quantisierungskennlinie – Funktion zur Abbildung von Analogwerten auf Digitalwerte, z. B. linear oder logarithmisch
• Signal-Rausch-Verhältnis in dB
• Dynamikumfang in dB
• Dynamische Parameter
• Intermodulationsstörungen in dB
• Monotonie – Ist ein Analog-Digital-Umsetzer monoton, so ist ausgeschlossen, dass eine Vergrößerung des Eingangssignals einen kleineren Ausgangscode zur Folge hat. Diese Eigenschaft ist beispielsweise für Anwendungen wichtig, in denen der Analog-Digital-Umsetzer innerhalb eines Regelkreises arbeitet.
• Betriebsstrom - schnelle Umsetzer arbeiten meist mit höheren Strömen

Siehe auch

• Abtast-Halte-Schaltung (Sample and hold circuit)
• Alias-Effekt und Antialiasing
• Digital-Analog-Umsetzer
• Nyquist-Theorem
• Spiegelfrequenz
• Quantisierung und Quantisierungsrauschen
• Dither
• Digitale Signalverarbeitung
• Digitale Messtechnik
• Vielkanalanalysator

Literatur

• Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 12. Auflage, Springer, Heidelberg 2002, ISBN 3-540-42849-6

Weblinks

• TU Ilmenau: Script AD- und DA-Umsetzer – pdf (PDF; 1,14 MB)
• Eine Einführung in Delta-Sigma-Wandler
• AD-Wandler in „Angewandte Mikroelektronik“ - Grundlagen
• Datenblatt des Flash-Wandlers MAX108 (PDF; 1,23 MB)
• Vollständige Beschreibung eines nur mit diskreten Transistoren aufgebauten 14 Bit A/D-Wandlers in einer digitalen Personenwaage, die als Studienprojekt/Spaßprojekt an der TU-Berlin gebaut wurde