- Karamatanotation
-
Die Stirling-Zahlen erster und zweiter Art, benannt nach James Stirling, werden in der Kombinatorik und der theoretischen Informatik verwendet.
Inhaltsverzeichnis
Notation
Für die Stirlingzahlen existieren mehrere Notationen. Stirlingzahlen der ersten Art werden mit kleinem s bezeichnet oder übereinander in eckigen Klammern geschrieben, Stirlingzahlen der zweiten Art werden mit großem S bezeichnet oder übereinander in geschweiften Klammern geschrieben:
Die Klammernotation wurde 1935 von Jovan Karamata in Analogie zu den Binomialkoeffizienten
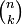 eingeführt und später von Donald Knuth populär gemacht. Sie wird auch Karamata-Notation genannt.
eingeführt und später von Donald Knuth populär gemacht. Sie wird auch Karamata-Notation genannt.Stirling-Zahlen erster Art
Die Stirling-Zahl erster Art sn,k ist die Anzahl der Permutationen einer n-elementigen Menge, die genau k Zykeln haben.
Beispiel
Die Menge {a,b,c,d} mit n = 4 Elementen kann auf folgende Weisen auf k = 2 Zykeln aufgeteilt werden:
Also ist s4,2 = 11.
Berechnung
Es gilt die rekursive Formel
mit den Anfangsbedingungen
- s0,0 = 1 = sn,n und sn,0 = 0 = s0,k für alle
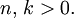
Insbesondere gilt sn,1 = (n − 1)! und
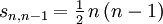 für alle n > 0.
für alle n > 0.Stirling-Zahlen zweiter Art
Die Stirling-Zahl zweiter Art Sn,k ist die Anzahl der k-elementigen Partitionen einer n-elementigen Menge, also die Anzahl der Möglichkeiten, eine n-elementige Menge in k nichtleere disjunkte Teilmengen aufzuteilen.
Beispiel
Die Menge {a,b,c,d} mit n = 4 Elementen kann auf folgende Weisen in k = 2 nichtleere disjunkte Teilmengen zerlegt werden:
- {{a,b},{c,d}}, {{a,c},{b,d}}, {{a,d},{b,c}}, {{a,b,c},{d}}, {{a,b,d},{c}}, {{b,c,d},{a}}, {{a,c,d},{b}}
Also ist S4,2 = 7.
Berechnung
Es gelten die explizite Formel
und die rekursive Formel
mit den Anfangsbedingungen
- S0,0 = 1 = Sn,n und Sn,0 = 0 = S0,k für alle
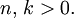
Insbesondere gilt Sn,1 = 1, Sn,2 = 2n − 1 − 1 und
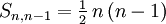 für alle n > 0.
für alle n > 0.Beweis
Es sei a ein fest gewähltes Element der n-elementigen Menge M. Die k-Partitionen von M können nun danach klassifiziert werden, ob {a} ein Element der Partition ist oder nicht.
Trifft dies zu, so bleiben ohne {a} noch alle Sn − 1,k − 1 möglichen (k − 1)-Partitionen aus den übrigen n − 1 Elementen von M.
Ist
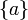 kein Element der Partition, erhält man nach Entfernung von a alle Sn − 1,k möglichen k-Partitionen der übrigen n − 1 Elemente von M. Da a in jeder der Möglichkeiten Element eines der Elemente der k-Partition ist und es dafür k Möglichkeiten gibt, sind es insgesamt
kein Element der Partition, erhält man nach Entfernung von a alle Sn − 1,k möglichen k-Partitionen der übrigen n − 1 Elemente von M. Da a in jeder der Möglichkeiten Element eines der Elemente der k-Partition ist und es dafür k Möglichkeiten gibt, sind es insgesamt 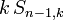 Möglichkeiten, also
Möglichkeiten, also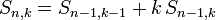 .
.
Alternative Herleitung
Es seien V der Vektorraum aller reell- oder komplexwertigen Polynome und Vm der Unterraum der Polynome mit Grad
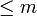 . Weiterhin seien
. Weiterhin seienund
Basen für Vm. So gelten folgende Beziehungen:
So können alternativ die Stirling-Zahlen 1. und 2. Art erzeugt werden, mit dem Unterschied, dass hier andere Vorzeichen auftreten als in den zuvor gegebenen Definitionen.
Analogie zu den Binomialkoeffizienten
Die Karamata-Notation betont die Analogie zu den Binomialkoeffizienten:
Für Binomialkoeffizienten gilt bekanntlich
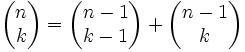 .
.
Entsprechend lassen sich die Stirling-Zahlen in einem Dreiecksschema ähnlich dem pascalschen Dreieck anordnen.
Dreieck für Stirling-Zahlen erster Art (erste Zeile n = 1, erste Spalte k = 1):
1 1 1 2 3 1 6 11 6 1 24 50 35 10 1 120 274 225 85 15 1 720 1764 1624 735 175 21 1 ... ... ... ... ... ... ... 1
Dreieck für Stirling-Zahlen zweiter Art (erste Zeile n = 1, erste Spalte k = 1):
1 1 1 1 3 1 1 7 6 1 1 15 25 10 1 1 31 90 65 15 1 1 63 301 350 140 21 1 1 ... ... ... ... ... ... 1
Gegenseitige Darstellung
Die Stirlingzahlen erster und zweiter Art lassen sich jeweils durch die anderen darstellen:
und
Literatur
- Manfred Wolff, Peter Hauck, Wolfgang Küchlin: Mathematik für Informatik und BioInformatik. Springer-Verlag, Berlin Heidelberg New-York, S.50, ISBN 3-540-20521-7
- Martin Aigner: Combinatorial Theory. Springer-Verlag, Originally published as volume 234 in the series: Grundlehren der mathematischen Wissenschaften, Reprint of the 1st ed. Berlin Heidelberg New York 1979, 1997, ISBN 978-3-540-61787-7
Weblinks
- Eric W. Weisstein: Stirling-Zahl erster Art auf MathWorld (englisch)
- Eric W. Weisstein: Stirling-Zahl zweiter Art auf MathWorld (englisch)
- Eric W. Weisstein: Stirling-Transformation auf MathWorld (englisch)
- Stirling-Zahlen erster Art: Folge A130534 in OEIS ohne Vorzeichen, Folge A008275 in OEIS mit Vorzeichen (englisch)
- Stirling-Zahlen zweiter Art: Folge A008277 in OEIS (englisch)
Wikimedia Foundation.

![s_{n,k} = \left[\begin{smallmatrix} n \\ k \end{smallmatrix}\right]](/pictures/dewiki/101/e20ce8a2082e6a8fc0f07e2d46175e03.png)
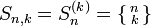
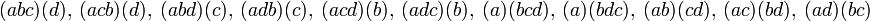
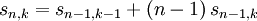
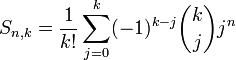
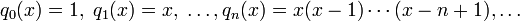
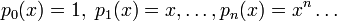
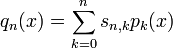
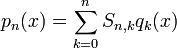
![\left[\begin{matrix} n \\ k \end{matrix}\right] =
\left[\begin{matrix} n-1 \\ k-1 \end{matrix}\right]
+ (n-1) \left[\begin{matrix} n-1 \\ k \end{matrix}\right]](/pictures/dewiki/97/a86b6489304dc11c398fbde79a146240.png)
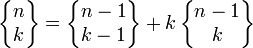
![\left[{n\atop k}\right] = (-1)^{n-k} \sum_{j=0}^{n-k} (-1)^j {n-1+j \choose n-k+j} {2n-k \choose n-k-j} \left\{ {n-k+j \atop j} \right\}](/pictures/dewiki/52/4eb4cf69c5a104a0e2f347ece52dad0e.png)
![\left\{{n\atop k}\right\} = \sum_{j=0}^{n-k} (-1)^{n-k+j} {n-1+j \choose n-k+j} {2n-k \choose n-k-j} \left[ {n-k+j \atop j} \right].](/pictures/dewiki/48/0e9ad1c7f74e4decc6c0c5a7ebb78a5a.png)