- Kehrbruch
-
 Graph der Kehrwertfunktion (Hyperbel)
Graph der Kehrwertfunktion (Hyperbel)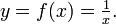
Der Kehrwert, auch Kehrzahl, einer Zahl ist diejenige Zahl, die mit sich selbst multipliziert genau eins ergibt. Den Kehrwert eines Bruches erhält man, wenn man bei diesem Nenner und Zähler miteinander vertauscht. Eine alternative Bezeichnung ist reziproker Wert.
Der Kehrwert der natürlichen Zahl n ist
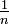 , also ein Stammbruch.
, also ein Stammbruch.Allgemein ist der Kehrwert eines rationalen Bruchs
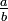 mit
mit 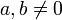 gleich
gleich 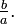 Null hat keinen reellen Kehrwert.
Null hat keinen reellen Kehrwert.Da jede von 0 verschiedene Zahl x als Bruch
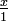 geschrieben werden kann, beträgt ihr Kehrwert
geschrieben werden kann, beträgt ihr Kehrwert 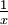 oder x − 1.
oder x − 1.Die Kehrwertfunktion ist eine Involution, d. h. der Kehrwert des Kehrwerts von a ist wieder a.
Beispiele
Der Kehrwert des Bruchs
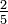 ist
ist 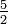 .
.Verallgemeinerung
Eine Verallgemeinerung des Kehrwerts ist das multiplikativ Inverse x − 1 eines Elements x eines Ringes, das durch die Eigenschaft
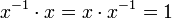 definiert ist.
definiert ist.Siehe auch
Wikimedia Foundation.
