Kehrwert

Zähler und Nenner eines Bruchs

Der Graph der Kehrwertfunktion ist eine Hyperbel mit der Gleichung $y=f(x)=\tfrac1x.$

Wenn man eine von 0 verschiedene Zahl mit ihrem Kehrwert (manchmal auch reziproker Wert, Kehrzahl oder Kehrbruch genannt) multipliziert, so ist das Produkt die Zahl 1. Den Kehrwert eines Bruches erhält man, indem man bei diesem Nenner und Zähler miteinander vertauscht.

Der Kehrwert einer natürlichen Zahl n ist $\tfrac 1n$, also ein Stammbruch.

Der Kehrwert einer rationalen Zahl $\tfrac ab$ mit $a, b\neq 0$ ist gleich der rationalen Zahl $\tfrac ba.$ 0 hat keinen Kehrwert.

Eine wichtige Anwendung der Kehrwertbildung ist die Regel zum Dividieren durch einen Bruch: Durch einen Bruch wird geteilt, indem man mit seinem Kehrwert multipliziert. Siehe auch Bruchrechnung!

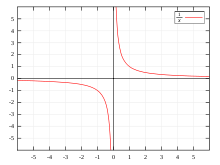
Da jede von 0 verschiedene Zahl x als Bruch $\tfrac{x}{1}$ geschrieben werden kann, ist ihr Kehrwert gleich $\tfrac{1}{x}$ (wofür man auch x ^{− 1} schreibt).

Die Kehrwertfunktion ist eine Involution, d. h. der Kehrwert des Kehrwerts von a ist wieder a.

Beispiele

• Der Kehrwert des Bruches $\tfrac{2}{5}$ ist $\tfrac{5}{2}$.
• Der Kehrwert von 2 ist $\tfrac{1}{2}$.
• Der Kehrwert von $-\tfrac{2}{3}$ ist $-\tfrac{3}{2}$.

Verallgemeinerung

Eine Verallgemeinerung des Kehrwerts ist das multiplikativ Inverse x ^{− 1} einer Einheit x eines unitären Ringes. Es ist durch die Eigenschaft $x^{-1}\cdot\ x=x\cdot\ x^{-1}=1$ definiert, wobei 1 das Einselement des Ringes bezeichnet. Wenn es sich z. B. um einen Ring von Matrizen handelt, so ist das Einselement nicht die Zahl 1, sondern die Einheitsmatrix).

Weblinks

 Wiktionary: Kehrwert – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Literatur

Hintergrundwissen für Lehramtsstudenten zur Arithmetik:

• Friedhelm Padberg: Arithmetik. Didaktik der Mathematik, Mathematik Primarstufe. Band I, Spektrum Akademischer Verlag, 1976, ISBN 9783827401991.