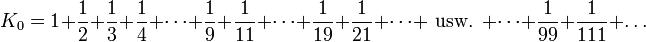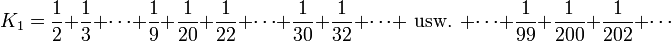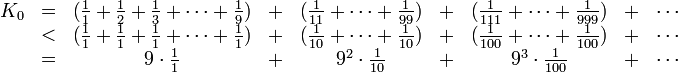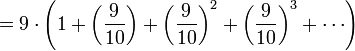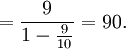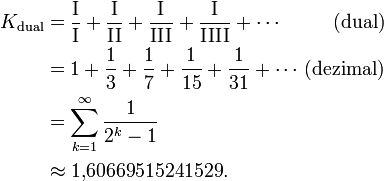Kempnerreihe

In der Mathematik bezeichnen die zehn Kempner-Reihen diejenigen Reihen, die dadurch entstehen, dass man aus der harmonischen Reihe 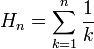$H_n=\sum_{k=1}^n \frac1k$ alle Summanden entfernt, die eine bestimmte dezimale Ziffer in ihrem Nenner enthalten. Die Kempner-Reihen gehören daher zu den subharmonischen Reihen.

Lässt man etwa alle Summanden weg, deren Nenner die Ziffer 0 in seiner Dezimalschreibweise enthält, ergibt sich die Kempner-Reihe K₀ als

$K_0=1+\frac12+\frac13+\frac14+\cdots+\frac19+\frac1{11}+\cdots+\frac1{19}+\frac1{21}+\cdots+\text{ usw. }+\cdots+\frac1{99}+\frac1{111}+\ldots$

Oder durch Auslassen der Summanden mit einer 1 im Nenner:

$K_1=\frac12+\frac13+\cdots+\frac19+\frac1{20}+\frac1{22}+\cdots+\frac1{30}+\frac1{32}+\cdots+\text{ usw. }+\cdots+\frac1{99}+\frac1{200}+\frac1{202}+\cdots$

Sie wurden erstmals von A. J. Kempner 1914 beschrieben.^[1]

Das Interessante an diesen Reihen ist, dass alle zehn konvergieren, obwohl die harmonische Reihe selbst nicht konvergiert. Dies wurde von Kempner bewiesen; daher werden die Reihen oft Kempnerreihen genannt.

Beweis der Konvergenz

Für die Kempner-Reihe K₀ sind

• im einstelligen Nennerbereich 1 bis 9 genau $\!\ 9$ Nenner (alle) zulässig;
• im zweistelligen Nennerbereich 10 bis 99 genau 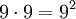$9\cdot 9=9^2$ Nenner (neun Ziffern an der ersten Stelle mal neun Ziffern an der zweiten Stelle möglich) zulässig;
• im dreistelligen Nennerbereich 100 bis 999 genau 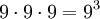$9\cdot 9\cdot 9=9^3$ Nenner zulässig; usw.,

allgemein sind

• im n-stelligen Nennerbereich 10^{n − 1} bis 10ⁿ − 1 genau 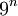$\!\ 9^n$ Nenner zulässig.

Die 9 zulässigen einstelligen Nennerwerte sind allesamt größergleich 1, daher sind die Brüche in der Reihe jeweils kleinergleich 1; die 9² zulässigen zweistelligen Nenner sind alle größergleich 10, daher sind die entsprechenden Brüche alle kleinergleich 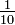$\tfrac1{10}$; die 9³ dreistelligen zulässigen Nenner sind jeweils größergleich 100, daher sind die entsprechenden Brüche allesamt kleinergleich 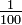$\tfrac1{100}$; usw.

Das ergibt die obere Schranke

$\begin{matrix} K_0&=&(\frac11+\frac12+\frac13+\cdots+\frac19)&+&(\frac1{11}+\cdots+\frac1{99})&+&(\frac1{111}+\cdots+\frac1{999})&+&\cdots \\ &<& (\frac11+\frac11+\frac11+\cdots+\frac11)&+& (\frac1{10}+\cdots+\frac1{10})&+& (\frac1{100}+\cdots+\frac1{100})&+&\cdots \\ &=& 9\cdot\frac11 &+& 9^2\cdot\frac1{10}&+&9^3\cdot\frac1{100}&+&\cdots \end{matrix}$

$= 9\cdot \left(1+\left(\frac9{10}\right)+\left(\frac9{10}\right)^2+\left(\frac9{10}\right)^3+\cdots\right)$

$=\frac9{1-\frac9{10}}=90.$

(Bei der Reihe in der vorletzten Zeile handelt es sich um eine konvergente geometrische Reihe)

Damit konvergiert K₀ und es gilt die (ziemlich großzügige) Schranke

K₀ < 90.

Der Beweis der Konvergenz der anderen Reihen verläuft analog, es ist aber zu beachten, dass im einstelligen Nennerbereich nur 8 Werte, im zweistelligen Nennerbereich aber 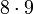$8\cdot 9$ Nennerwerte zulässig sind, da an der ersten Stelle sowohl die Null als auch die entsprechende Ziffer, an der zweiten Stelle aber nur die entsprechende Ziffer "verboten" sind, usw.; insgesamt ergibt sich dadurch die Schranke 80.

Werte

Die Reihen konvergieren extrem langsam.

Näherungswerte

Ausgelassene Ziffer	Näherungswert[2]
0	23,10344
1	16,17696
2	19,25735
3	20,56987
4	21,32746
5	21,83460
6	22,20559
7	22,49347
8	22,72636
9	22,92067

Effiziente Berechnungsmöglichkeiten

Aufgrund der ziemlich langsamen Konvergenz benötigt man schnelle und effiziente Berechnungsalgorithmen, vgl. ^[3].

Erweiterungen

n-faches Auftreten

F. Irwin verallgemeinerte das Resultat der Konvergenz der zehn Kempner-Reihen, indem er bewies, dass alle Reihen, die über die Kehrwerte aller natürlicher Zahlen, in denen die Ziffer x₀ genau n₀ mal, die Ziffer x₁ genau n₁, usw. auftreten, ebenfalls konvergieren.^[4]

Die Summe der Kehrwerte der natürlichen Zahlen, in denen genau eine 9 vorkommt, beträgt etwa 23,044287080747848319. Dieser Wert ist größer als Kempners K₉, obwohl diese mit größeren Summanden beginnt. Ein extemeres Beispiel dafür ist die Summe der Kehrwerte der natürlichen Zahlen, in denen einhundert Nullen vorkommen, sie beginnt mit dem Summanden 1 / 10¹⁰⁰ und ist dennoch größer als etwa K₉.^[3]

Zusammenhängende Ziffernfolgen

Eine Möglichkeit, die harmonische Reihe weit weniger auszudünnen, ist, nur alle Summanden herauszunehmen, deren Nenner irgendwo eine bestimmte zusammenhängende Ziffernfolge - etwa 314 - enthält. Auch derartige Reihen konvergieren - in diesem Fall ergibt sich ein Grenzwert von etwa 2299,829782.^[5]

In anderen Stellenwertsystemen

Es gibt natürlich auch analoge Reihen in anderen Stellenwertsystemen. Die duale Kempner-Reihe etwa entsteht durch Streichen aller Summanden, die eine O in ihrer Dualdarstellung enthalten. Alle Dualzahlen zu streichen, in denen eine I vorkommt, geht nicht. Die einzige duale Kempnerreihe ist also

$\begin{alignat}{2} K_{\text{dual}} &amp;amp;= \frac{\rm I}{\rm I}+\frac{\rm I}{\rm II}+\frac{\rm I}{\rm III}+\frac{\rm I}{\rm IIII}+\cdots &amp;amp;\text{(dual)} \\ &amp;amp;= 1+\frac13+\frac17+\frac1{15}+\frac1{31}+\cdots &amp;amp;\text{ (dezimal)}\\ &amp;amp;= \sum_{k=1}^\infty \frac1{2^k-1}\\ &amp;amp;\approx 1{,}60669515241529. \end{alignat}$

Zum Beweis der Konvergenz betrachte man die unendliche konvergente geometrische Reihe 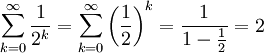$\sum_{k=0}^\infty\frac1{2^k} =\sum_{k=0}^\infty\left(\frac12\right)^k = \frac1{1-\frac12}=2$ als obere Schranke.

Quellen

1. ↑ A. J. Kempner: A Curious Convergent Series. In: Amer. Math. Monthly, Band 21 Nr. 2, Mathematical Association of Americam, Washington 1914, Seiten 48–50, ISSN 00029890.
2. ↑ Eric W. Weisstein: Kempner Series auf MathWorld (englisch)
3. ↑ ^{a b} Summing the Curious Series of Kempner and Irwin, arxiv
4. ↑ F. Irwin: A Curious Convergent Series. In: Amer. Math. Monthly. Band 23, 1916, Seiten 149-152.
5. ↑ R. Baillie, T. Schmelzer: Summing Kempner's Curious (Slowly-Convergent) Series. 20. Mai 2008; vgl. in Wolfram Libary Archive

• Julian Havil: Gamma: Eulers Konstante, Primzahlstrände und die Riemannsche Vermutung. Springer, Berlin 2007, S. 42ff. ISBN 978-3-540-48495-0
• Folgen A082839 und A082830 in OEIS