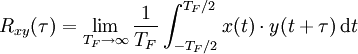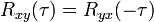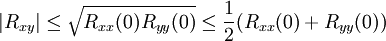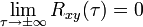KKF — Die Korrelation beschreibt die lineare Beziehung zwischen zwei oder mehr statistischen Variablen. Wenn sie besteht, ist noch nicht gesagt, ob eine Größe die andere kausal beeinflusst, ob beide von einer dritten Größe kausal abhängen oder ob sich… … Deutsch Wikipedia
kkf — ISO 639 3 Code of Language ISO 639 2/B Code : ISO 639 2/T Code : ISO 639 1 Code : Scope : Individual Language Type : Living Language Name : Kalaktang Monpa … Names of Languages ISO 639-3
KKF — abbr. Kreitman Foundation Fellowship … Dictionary of abbreviations
Kontemporäre Korrelation — Die Korrelation beschreibt die lineare Beziehung zwischen zwei oder mehr statistischen Variablen. Wenn sie besteht, ist noch nicht gesagt, ob eine Größe die andere kausal beeinflusst, ob beide von einer dritten Größe kausal abhängen oder ob sich… … Deutsch Wikipedia
Korrelationen — Die Korrelation beschreibt die lineare Beziehung zwischen zwei oder mehr statistischen Variablen. Wenn sie besteht, ist noch nicht gesagt, ob eine Größe die andere kausal beeinflusst, ob beide von einer dritten Größe kausal abhängen oder ob sich… … Deutsch Wikipedia
Korrelationsintegral — Die Korrelation beschreibt die lineare Beziehung zwischen zwei oder mehr statistischen Variablen. Wenn sie besteht, ist noch nicht gesagt, ob eine Größe die andere kausal beeinflusst, ob beide von einer dritten Größe kausal abhängen oder ob sich… … Deutsch Wikipedia
Korrelationsoperator — Die Korrelation beschreibt die lineare Beziehung zwischen zwei oder mehr statistischen Variablen. Wenn sie besteht, ist noch nicht gesagt, ob eine Größe die andere kausal beeinflusst, ob beide von einer dritten Größe kausal abhängen oder ob sich… … Deutsch Wikipedia
Korrelativ — Die Korrelation beschreibt die lineare Beziehung zwischen zwei oder mehr statistischen Variablen. Wenn sie besteht, ist noch nicht gesagt, ob eine Größe die andere kausal beeinflusst, ob beide von einer dritten Größe kausal abhängen oder ob sich… … Deutsch Wikipedia
Korrelativität — Die Korrelation beschreibt die lineare Beziehung zwischen zwei oder mehr statistischen Variablen. Wenn sie besteht, ist noch nicht gesagt, ob eine Größe die andere kausal beeinflusst, ob beide von einer dritten Größe kausal abhängen oder ob sich… … Deutsch Wikipedia
Korreliert — Die Korrelation beschreibt die lineare Beziehung zwischen zwei oder mehr statistischen Variablen. Wenn sie besteht, ist noch nicht gesagt, ob eine Größe die andere kausal beeinflusst, ob beide von einer dritten Größe kausal abhängen oder ob sich… … Deutsch Wikipedia
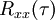 und
und 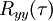 .
.