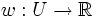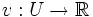Knapsack-Problem

Das Rucksackproblem: Welche der Gewichte können in den Rucksack mit Maximallast von 15 kg gepackt werden, so dass der Geldwert maximal wird? (Lösung in diesem Fall: Alle Gewichte außer dem schwersten einpacken.)

Das Rucksackproblem (oft mit RUCKSACK, KNAPSACK bezeichnet) ist ein Optimierungsproblem der Kombinatorik. Aus einer Menge von Objekten, die jeweils ein Gewicht und einen Nutzwert haben, soll eine Teilmenge ausgewählt werden, deren Gesamtgewicht eine vorgegebene Gewichtsschranke nicht überschreitet. Unter dieser Bedingung soll der Nutzwert der ausgewählten Objekte maximiert werden.

Die Entscheidungsvariante des Rucksackproblems fragt, ob ein zusätzlich vorgegebener Nutzwert erreicht werden kann. Sie gehört zur Liste der 21 klassischen NP-vollständigen Probleme, von denen Richard Karp 1972 die Zugehörigkeit zu dieser Klasse zeigen konnte.

In der Kryptographie wird häufig eine andere Entscheidungsvariante betrachtet. Dabei werden nur die Gewichte betrachtet und es wird gefragt, ob es eine Teilmenge der Objekte gibt, die einen vorgebenen Gewichtswert genau erreicht. Diese Problemvariante wird auch als SUBSET-SUM bezeichnet. Basierend auf dieser Variante wurde das Public-Key-Kryptoverfahren Merkle-Hellman-Kryptosystem entwickelt, das sich allerdings als nicht besonders sicher herausstellte.

Anschauung

Das Rucksackproblem hat seinen Namen aus folgender Anschauung heraus erhalten: Es sind verschiedene Gegenstände mit einem bestimmten Gewicht und einem Nutzwert gegeben. Aus diesen Gegenständen soll nun eine Auswahl getroffen werden, die in einen Rucksack mit einer vorgegebenen Gewichtsschranke mitgenommen werden können. In der Literatur wird zur Veranschaulichung auch gerne der Dieb herangezogen, der nur einen kleinen Teil der Beute im Rucksack abtransportieren kann und nun versucht, das Maximum an Nutzwert herauszuschlagen.

Mathematische Formulierung

Gegeben sind eine endliche Menge von Objekten U. Durch eine Gewichtsfunktion w und die Nutzenfunktion v wird den Objekten ein Gewicht und ein Nutzwert zugeordnet:

$w:U\rightarrow\mathbb{R}$

$v:U\rightarrow\mathbb{R}$

Des Weiteren gibt es eine vorgegebene Gewichtsschranke $B \in\mathbb{R}$.

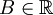Gesucht ist eine Teilmenge 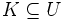$K\subseteq U$, die die Bedingung

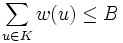$\sum_{u\in K} w(u) \le B$ einhält und die Zielfunktion 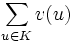$\sum_{u\in K} v(u)$ maximiert.

Lösung mittels dynamischer Programmierung

Sind Gewichte und Nutzen ganzzahlig, so lässt sich der optimale Wert des Rucksackproblems auch mittels dynamischer Programmierung lösen. Seien dazu 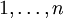$1,\ldots,n$ die Elemente von U.

Eingabe: U, B, w, v wie oben beschrieben
 R := [1…(n+1), 0…B]-Matrix, mit Einträgen 0
 FOR i = n … 1
    FOR j = 1 … B
       IF w(i) <= j 
          R[i,j] := max( v(i) + R[i+1, j-w(i)], R[i+1,j] )
       ELSE
          R[i,j] := R[i+1,j]
Ausgabe: R[1,B]

In jeder Speicherzelle R(i,j) ist der maximale Nutzwert bei maximal möglichen Gesamtgewicht von j bei Berücksichtigung einer Teilmenge von Gegenständen aus der Teilsequenz [i..n] der Gesamtsequenz aller Gegenstände [1..n]. Also ist der maximale Nutzwert bei Berücksichtigung einer Teilmenge aller Gegenstände in der Zelle R(1,B) nach Beendigung des Algorithmus gespeichert.

In jeder Zeile i der Matrix R wird über die beiden Fälle optimiert, ob der Nutzwert maximal vergrößert werden kann, wenn der Gegenstand i mit dem Gewicht w(i) dem Rucksack hinzugefügt oder er nicht aufgenommen wird. Im ersten Fall erhöht sich der Nutzwert um v(i).

Um den Inhalt des Rucksacks mit dem maximalen Nutzwert zu bestimmen, kann er rekonstruiert werden, indem die Berechnung des Optimums in R(1,B) mittels Backtracking zurückverfolgt wird.

Die Korrektheit folgt aus folgender Beobachtung:

Sei 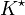$K^\star$ eine optimale Lösung. Dann ist 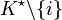$K^\star\backslash\{i\}$ eine optimale Lösung für die Instanz 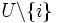$U\backslash\{i\}$ mit Maximalgewicht B − w(i). Der Algorithmus benötigt aufgrund der verschachtelten for-Schleifen, die über n und B iterieren, eine Laufzeit von 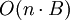$O(n\cdot B)$. Hierbei ist zu beachten, dass B eine zu seiner Eingabelänge exponentiell wachsende Größe und somit die Laufzeit pseudopolynomiell ist.

Anwendungen

Viele reale Fragestellungen lassen sich auf dieses Problem bzw. den Lösungsansatz zurückführen. Oft steht eine begrenzte Kapazität zur Verfügung, welche nicht die gesamte Nachfrage befriedigen kann. Man denke z. B. an einen Lkw, der viele verschiedene Güter – mit einem bestimmten Gewinn – transportieren soll, aber wegen der begrenzten Lademenge nicht alle Güter aufnehmen kann. Der Besitzer des Lkws wird die Ladung so wählen wollen, dass der Gewinn maximal ausfällt.

Literatur

• Kellerer, Hans; Pferschy, Ulrich; Pisinger, David: Knapsack Problems. Springer, 2004, ISBN 978-3-540-40286-2. 
• Martello, Silvano; Toth, Paolo: Knapsack problems: algorithms and computer implementations. J. Wiley, Chichester 1990, ISBN 978-0-471-92420-3 (Buch als PDF und Fortran-Quelltext zum Buch). 

Weblinks

• „Algorithmus der Woche“ zum Rucksackproblem - Zum Thema: Das Informatikjahr - Das Wissenschaftsjahr 2006