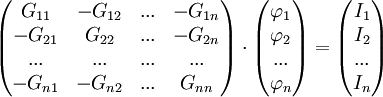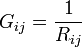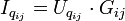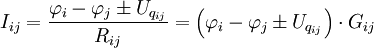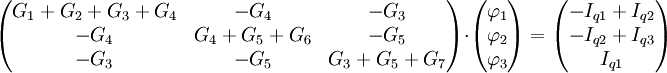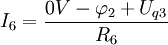Knotenspannungsverfahren

Das Knotenpotentialverfahren (auch Knotenspannungsanalyse oder Knotenadmittanzverfahren) ist ein Verfahren zur Netzwerkanalyse in der Elektrotechnik. Mit dieser Methode lassen sich die Knotenpotentiale eines elektrischen Netzwerks aus linearen Bauelementen bestimmen.

Matrix des linearen Gleichungssystem

$\begin{pmatrix} G_{11} &-G_{12} & ... & -G_{1n} \\ -G_{21} & G_{22} & ... & -G_{2n} \\ ... & ... & ... & ... \\ -G_{n1} &-G_{n2} & ... & G_{nn} \end{pmatrix} \cdot \begin{pmatrix} \varphi_1 \\ \varphi_2 \\ ... \\ \varphi_n \end{pmatrix} = \begin{pmatrix} I_1 \\ I_2 \\ ... \\ I_n \end{pmatrix}$

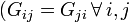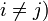Die Leitwertmatrix ist eine symmetrische Matrix. Folglich sind die gegenüberliegenden Koppelleitwertwerte (bezüglich der Hauptdiagonale) identisch $\left( G_{ij} = G_{ji} \, \forall \, i,j \right.$ mit $\left. i \neq j \right)$. Das muss so sein, weil sich diese Koppelleitwerte in beiden Fällen zwischen denselben Knoten befinden. Im Gegensatz zu den positiven Summenleitwerte auf der Hauptdiagonalen sind alle Koppelleitwerte negativ.

Anwendung des Verfahrens

Das Verfahren wird gewöhnlich zur Bestimmung eines Stromes in einem Zweig verwendet. Gegenüber der Zweigstromanalyse werden bei diesem Verfahren so viele Gleichungen eingespart, wie das Netzwerk unabhängige Maschen besitzt. Im folgenden werden alle Schritte zum gesuchten Wert aufgezeigt. Dieses Verfahren gilt auch für komplexe und magnetische Netzwerke, sofern nur lineare Bauelemente vorkommen.

Knotenpotentiale und Bezugsknoten festlegen

Bei einem Netzwerk mit k Knoten gibt es k-1 unabhängige Knotengleichungen. Für einen Knoten muss keine Gleichung aufgestellt werden, da sich dessen Gleichung aus den Gleichungen der anderen Knoten aufstellen ließe und damit linear abhängig wäre. Dieser Knoten ist deshalb der Bezugsknoten mit Nullpotential (Masse) und kann beliebig gewählt werden. Zweckmäßigerweise sollte der Knoten an einen Zweig mit gesuchten Spannungsabfall liegen, da so schon ein benötigtes Potential feststeht und das Gleichungssystem einmal weniger gelöst werden muss. Alle anderen Potentiale sind noch unbekannt und werden mit einem eindeutigen Variablennamen bezeichnet.

Umwandlung der Widerstände und Spannungsquellen

Thévenin-Norton-Äquivalent-Umwandlung

Die Zweigströme werden als Produkt aus Zweigleitwert und Knotenpotenzialdifferenz ausgedrückt. Deshalb werden die Zweigwiderstände durch deren Leitwerte ersetzt und die Spannungsquellen nach dem Norton-Theorem in Ersatzstromquellen umgeformt.

$G_{ij}=\frac {1}{R_{ij}}$

$I_{q_{ij}} = U_{q_{ij}} \cdot G_{ij}$

Ideale Spannungsquellen ohne Widerstand im Zweig können nicht umgeformt werden. Weiteres dazu im Punkt Behandlung von idealen Spannungsquellen.

Gleichungssystem aufstellen

Die Leitwertmatrix wird wie folgt aufgestellt:

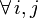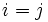• Auf der Hauptdiagonalen $\forall \, i,j$ mit $\!\, i = j$ steht die Summe der Leitwerte aller Zweige, die mit Knoten i verbunden sind.
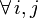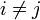• An den anderen Stellen $\forall \, i,j$ mit $i \neq j$ steht die negative Summe der Leitwerte zwischen den benachbarten Knoten i und j (Koppelleitwerte). Besteht keine direkte Verbindung zwischen zwei Knoten, wird an dieser Stelle eine Null eingetragen.

Im Vektor der Knotenpotentiale muss die gleiche Reihenfolge wie auf der Hauptdiagonalen der Leitwertmatrix eingehalten werden.

Im Vektor der Knotenströme auf der anderen Seite des Gleichungssystems steht die Summe der Ersatzstromquellen mit denen der jeweilige Knoten verbunden ist. Hinfließende Ströme gehen positiv, wegfließende Ströme gehen negativ in die Summe ein (es geht auch anders herum, es muss nur einheitlich für alle Knoten erfolgen). Sind keine Quellen mit dem Knoten verbunden, wird eine Null eingetragen.

Behandlung idealer Spannungsquellen

In sehr seltenen Fällen kann sich eine ideale Spannungsquelle (ohne Innen-/Zweigwiderstand) in einem Zweig zwischen zwei Knoten befinden. Dadurch ist die Spannungsdifferenz zwischen den beiden Knoten bekannt und ein Potential kann mit Hilfe des konstanten Wertes der Quellspannung aus dem anderen direkt berechnet werden. Dabei ist zu beachten, in welche Richtung die Spannung der Quelle abfällt:

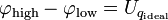$\varphi_{\text{high}} - \varphi_{\text{low}} = U_{q_{\text{ideal}}}$ mit Spannungsabfall von "high"-Knoten zu "low"-Knoten

Die Gleichung wird nach dem zu ersetzenden Potential umgeformt und in das Gleichungssystem eingesetzt. Falls einer der Knoten der Bezugsknoten ist, muss selbstverständlich das Potential des anderen ersetzt werden. Im Gleichungssystem wird der eingesetzte Term in jeder Zeile mit den Leitwerten in der zugehörigen Spalte multipliziert. Die Terme mit 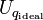$U_{q_{\text{ideal}}}$ werden auf die Seite der Stromquellen verschoben.

Das weitere Vorgehen ist nun abhängig von der Position des Bezugsknotens. Alle Zeilen der ersetzten Potentiale, deren ideale Spannungsquelle mit dem Bezugsknoten direkt verbunden ist, müssen gestrichen werden. Dadurch reduziert sich der Grad des Gleichungssystems mit jeder idealen Spannungsquelle am Bezugsknoten um Eins. Für alle anderen idealen Spannungsquellen wird in ihren Zweig ein unbekannter Zweigstrom eingeführt. Diese werden zunächst auf die Seite der Stromquellen nach dem gleichen Schema wie die Stromquellen eingetragen. Hinfließende addiert, Wegfließende subtrahiert. Abschließend werden die unbekannten Zweigströme auf die linke Seite gebracht. Für ideale Spannungsquellen ohne direkte Verbindung zum Bezugsknoten reduziert sich der Grad des Gleichungssystems folglich nicht, da für jedes entfallene Potential ein unbekannter Strom hinzukommt.

Gesuchte Potentiale berechnen

Zweig mit Spannungsquelle

Vor der Berechnung eines Zweigstromes müssen die Potenziale der beiden angrenzenden Knoten (φ_i und φ_j) bekannt sein. Dazu wird das Gleichungssystem für eines der Potentiale gelöst. Dies geschieht entweder mit Hilfe der Cramer’schen Regel oder durch das Gaußsche Eliminationsverfahren. Sollte einer davon der Bezugsknoten sein, muss nur ein Potential berechnet werden. Die Zweigspannung wird durch die Differenz der Knotenpotentiale für gewöhnlich so berechnet, dass die resultierende Zweigspannung in die vermutete Richtung des gesuchten Stroms abfällt. Der Wert einer eventuell vorhandenen Spannungsquelle im Zweig muss nach dem Maschensatz von der Zweigspannung subtrahiert werden, wenn ihre Spannung in Richtung Zweigspannung abfällt, oder addiert werden, wenn sie in entgegengesetzte Richtung verläuft. Das Ergebnis wird anschließend durch den Zweigwiderstand geteilt bzw. mit dem Zweigleitwert multipliziert, um den gesuchten Strom zu erhalten. Ein positiver Zweigstrom fließt in Richtung des Spannungsabfalls der Knotenpotenzialdifferenz, ein negativer Zweigstrom in entgegengesetzte Richtung.

$I_{ij} = \frac {\varphi_i - \varphi_j \pm U_{q_{ij}}}{R_{ij}} = \left( \varphi_i - \varphi_j \pm U_{q_{ij}} \right) \cdot G_{ij}$

Beispiel

Schaltung zur Demonstration des Knotenpotentialverfahrens

Gesucht ist I₆ in der rechts dargestellten Schaltung. Dieser wird nun Schritt für Schritt mit Hilfe des Knotenpotentialvefahrens berechnet.

• Knotenpotentiale und Bezugsknoten festlegen

Zur schnelleren Berechnung wird ein Knoten, mit dem der Zweig von I₆ verbunden ist, zum Bezugsknoten mit Nullpotential. In diesem Beispiel fiel die Entscheidung auf den unteren Knoten. Die restlichen drei Knoten werden mit φ₁, φ₂ und φ₃ bezeichnet. Wie hier im Falle des Bezugsknotens ist zu beachten, dass mehrere dargestellte Knoten praktisch nur ein Knoten sind, wenn sich auf den Zweigen zwischen ihnen keine Schaltungselemente befinden.

• Umwandlung der Widerstände und Spannungsquellen

In der Schaltung befinden sich zwei Spannungsquellen und eine Stromquelle. Die Spannungsquellen werden wie oben beschrieben in Ersatzstromquellen umgeformt.

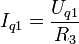$I_{q1} = \frac {U_{q1}}{R_3}$ und $I_{q3} = \frac {U_{q3}}{R_6}$

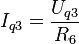
Zu beachten ist, dass die korrekte Stromrichtung bei den Stromquellen eingezeichnet wird. Außerdem ist nun der Strom durch G₆ nicht mehr gleich I₆, weil sich dieser nun auf die Zweige von G₆ und I_q3 aufteilt. Nach dem Ersetzen der Widerstände mit ihren Leitwerten ergibt sich die untere Schaltung im Bild.

• Gleichungssystem aufstellen

Nach den oben genannten Regeln wird nun das Gleichungssystem in Matrixform aufgestellt.

$\begin{pmatrix} G_1 + G_2 + G_3 + G_4 & -G_4 & -G_3 \\ -G_4 & G_4 + G_5 + G_6 & -G_5 \\ -G_3 & -G_5 & G_3 + G_5 + G_7 \end{pmatrix} \cdot \begin{pmatrix} \varphi_1 \\ \varphi_2 \\ \varphi_3 \end{pmatrix} = \begin{pmatrix} -I_{q1} + I_{q2} \\ -I_{q2} + I_{q3} \\ I_{q1} \end{pmatrix}$

• Gesuchte Potentiale berechnen

Da das Bezugspotential schon bekannt ist, wird nur noch das Potential φ₂ benötigt. Welches der beiden genannten Rechenverfahren verwendet wird, sei jedem selbst überlassen. An dieser Stelle wird lediglich auf die beiden Artikel der Verfahren verwiesen (Cramer’sche Regel, Gaußsches Eliminationsverfahren).

Mit Hilfe des berechneten Potentials folgt die Bestimmung des gesuchten Stroms I₆. Das Nullpotential wird durch 0V ausgedrückt. Die Potentialdifferenz wird in die vermutete Richtung von I₆ gebildet. Der Wert der Spannungsquelle U_q3 muss nach oben erwähnter Regel zur Differenz addiert werden.

$I_6 = \frac {0V - \varphi_2 + U_{q3}}{R_6}$

Anwendung

Das Knotenpotentialverfahren eignet sich hervorragend zur computerunterstützten Berechnung des Lösungsvektors, da sein Lineares Gleichungssystem durch einen einfacher zu programmierenden Algorithmus aufgestellt werden kann als beim Maschenstromverfahren, bei dem zunächst das Netzwerk graphentheoretisch nach einem vollständigen Baum abgesucht werden muss. Es bildet deshalb die Basis der meisten Rechnerprogramme zur Analyse Linearer Elektrischer Netzwerke. Allerdings ist die optimale Auswahl des zu verwendenden Netzwerkanalyseverfahrens abhängig von der Struktur des Netzwerks (Anzahl der Zweige verglichen mit der Anzahl der Knoten) und in der Praxis individuell für jedes Netzwerk.

Siehe auch

• Maschenstromverfahren
• Kirchhoffsche Regeln
• Netzwerkanalyse (Elektrotechnik)