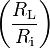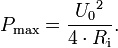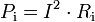- Konstantspannungsquelle
-
Als Spannungsquelle wird ein Gerät bezeichnet, das eine elektrische Spannung erzeugt oder eine Sekundärspannung aus einer Primärquelle ableitet. Eine Spannungsquelle ist eine Energiequelle, die abhängig vom angeschlossenen Verbraucher elektrischen Strom liefert. Man spricht umgangssprachlich auch von Stromversorgung, da die Quelle elektrische Energie zur Verfügung stellt. Eine Spannungsquelle kann auch ein Gegenstand sein, der lediglich ein elektrisches Feld erzeugen kann, dabei aber nur kurzzeitig oder in nicht verwertbarem Umfang zur Stromabgabe fähig ist. Zu den allgemein bekannten, technisch nicht verwertbaren Spannungsquellen zählen Gewitterwolken.
Inhaltsverzeichnis
Arten von Spannungsquellen
Gleich- und Wechselspannungsquellen
 Schaltzeichen gemäß DIN EN 60617-2 für eine ideale Gleichspannungsquelle mit der elektrischen Spannung U
Schaltzeichen gemäß DIN EN 60617-2 für eine ideale Gleichspannungsquelle mit der elektrischen Spannung UGleichspannungsquellen sind Energiequellen, deren Spannungsbetrag zeitlich konstant ist. Typische Gleichspannungsquellen sind z. B. Batterien, Akkumulatoren und Netzgeräte. Im Gegensatz dazu erzeugt eine Wechselspannungsquelle eine sich zeitlich periodisch verändernde Spannung. Zu diesen Quellen gehören z. B. Generatoren, Transformatoren, Signalgeneratoren und ebenfalls Netzgeräte. Auch das elektrische Energieversorgungsnetz stellt eine Wechselspannungsquelle dar.
Asymmetrische, bipolare und symmetrische Spannungsversorgungen
Hat eine Gleichspannungsquelle zwei Anschlüsse, von denen eine zum allgemeinen Bezugs- oder Massepotential erklärt wird, so spricht man von einer asymmetrischen Spannungsquelle.
Bei einer bipolaren Spannungsversorgung werden gleichzeitig eine positive und negative Spannung, bezogen auf ein gemeinsames Massepotential, z. B. + 15 V und − 10 V, bereitgestellt. Sind die positive und negative Spannung zudem gleich groß, so handelt es sich um eine symmetrische Spannungsversorgung. Diese bietet eine bessere Störunempfindlichkeit, weshalb sie insbesondere bei der Signalübertragung zur Anwendung gelangt. Ein einfaches Beispiel für eine symmetrische Spannungsquelle ist ein Transformator mit Mittenanzapfung.
Geregelte und gesteuerte Spannungsquellen
Geregelte Spannungsquellen beinhalten einen zusätzlichen elektronischen Schaltkreis, der die Ausgangsspannung auf den eingestellten Sollwert regelt. Durch die aktive Regelung werden Störeinflüsse durch variable elektrische Lasten, Schwankungen der Netzspannung oder Temperaturdrifts kompensiert. Dabei ist irrelevant, ob es sich bei der geregelten Spannung um eine Gleich- oder Wechselspannungsquelle handelt. Geregelte Gleichpannungsquellen werden mitunter als Konstantspannungsquellen, oder wenn sie besonders präzise sind als Referenzspannungsquellen bezeichnet. Im Gegensatz zu dem Modell der idealen Spannungsquelle ist jedoch der maximale Strom begrenzt. Überschreitet der Strom eine bestimmte Grenze, bricht die Spannung in der Regel schlagartig ein.
Kann die Regelung der Spannungsquelle extern beeinflusst werden, spricht man von einer gesteuerten Spannungsquelle.
Technische Beschreibungen
Grundlagen
In diesem Artikel werden folgende Bezeichnungen verwendet:
- Ausgangs- oder Klemmenspannung Ukl
- Quellenspannung U0, früher auch als Urspannung oder Elektromotorische Kraft (EMK) bezeichnet
U0 ist die maximale Spannung, die an den Klemmen anliegen kann - Kurzschlussstrom IK
IK ist der Strom, den die Quelle liefert wenn der Widerstand an den Klemmen gleich Null ist - Innenwiderstand Ri, auch als Quellwiderstand RQ bezeichnet
- Lastwiderstand RL, auch als Verbraucherwiderstand RV bezeichnet
Ideale und reale Spannungsquellen
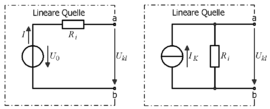
 Ersatzschaltbild einer realen Spannungsquelle (mit Verbraucher)
Ersatzschaltbild einer realen Spannungsquelle (mit Verbraucher)Als ideale Spannungsquelle wird eine Spannungsquelle bezeichnet, die unabhängig von der nachgeschalteten Last stets dieselbe Spannung abgibt. Klemmen- und Quellenspannung wären somit immer identisch, der Energievorrat der Quelle wird als unendlich angenommen. Da dies in der Praxis aber unmöglich zu erreichen ist, werden in technischen Berechnungen zumeist reale Spannungsquellen eingesetzt. Diese bestehen aus einer idealen Spannungsquelle, zu der ein in Reihe geschalteter Widerstand, der Innenwiderstand, angenommen wird. Dadurch kann bei Berechnungen der Einfluss von nachgeschalteten Lasten auf die tatsächlich anliegende Klemmenspannung der Quelle nachvollzogen werden. Je stärker die Quelle belastet wird, desto tiefer sinkt die an den Klemmen anliegende Spannung. In der Praxis kann der Innenwiderstand einer Spannungsquelle variieren, beispielsweise ist der Innenwiderstand einer neuen Batterie viel geringer als derjenige einer verbrauchten.
Der Innenwiderstand begrenzt zudem den maximalen Strom, der im Kurzschlussfall (RL=0) fließen kann. Der Kurzschlussstrom berechnet sich dann zu
Der maximale Strom ist also umso größer, desto kleiner der Innenwiderstand der Quelle ist.
Aus den hier aufgeführten Gründen ist es daher anzustreben, den Innenwiderstand für technische Spannungsquellen so klein wie möglich, am besten Ri=0, zu halten. Jedenfalls sollte er viel kleiner als der des Verbrauchers sein.
Kennlinien
Die Klemmenspannung einer Spannungsquelle als Funktion des entnommenen Stroms I wird grafisch als Kennlinie dargestellt.
- Bei einer idealen Spannungsquelle ist diese eine waagerechte Gerade
- Bei einer realen Quelle erhält man in der Regel eine geneigte Gerade
Die Quelle hat ein Verhalten, bei der die Spannung linear mit steigendem Strom abnimmt - Eine nichtlineare Quelle weist eine nichtlineare Kennlinie auf. Bei einer Solarzelle ist die Nichtlinearität infolge von Halbleitereffekten beträchtlich. Nur im flachen Bereich ihrer Kennlinie kann diese Quelle als Spannungsquelle angesehen werden, im steilen Bereich wird ihr Verhalten durch eine Stromquelle angemessener beschrieben. Für eine Gesamtbehandlung ist eine eigenständige Darstellung erforderlich, sodass nichtlineare Fälle nachfolgend nicht behandelt werden.
Parallel- und Reihenschaltung von Spannungsquellen
Reihenschaltung
Bei Reihenschaltung mehrerer Spannungsquellen ergibt sich die Gesamtspannung aus der Summe der Leerlaufspannungen der einzelnen Spannungsquelle. Ebenso ist der Gesamtquellwiderstand gleich der Summe der einzelnen Innenwiderstände. Der Strom ist für alle Quellen in der Frequenz, Phase und Amplitude identisch.
Parallelschaltung
Wird mehr Strom vom Verbraucher benötigt, als eine einzelne Quelle liefern kann, sodass eine Parallelschaltung von Spannungsquellen erforderlich wird, so ist dies nur bedingt mit realen Quellen möglich. Dazu müssen bei Bedarf Quellenwiderstände durch externe in die Leitungen geschaltete Widerstände nachgebildet werden. Diese müssen so groß sein, dass durch ihre Spannungsverluste die Spannung am Verbraucher kleiner wird als die kleinste der Leerlaufspannungen. Zusätzlich ist darauf zu achten, dass alle parallelgeschalteten Spannungsquellen bezüglich der Spannung:
- Den gleichen Betrag haben
- Das gleiche Vorzeichen (Polung) aufweisen
- Erdfrei sind oder am gleichen Pol geerdet sind. Bei mehr als einem Erdpunkt können geringe Differenzströme fließen (siehe Brummschleife)
- Wechselspannungsquellen die gleiche Phase haben
Werden diese Punkte nicht beachtet führt dies zu einem meist unerwünschten Stromfluss zwischen den Quellen. Je nach Stromhöhe und/oder Ausführung der Spannungsquelle kann dies zur Zerstörung einzelner Teilquellen führen. Diese Kriterien können auch mit entsprechenden elektronischen Schutzschaltungen, die die Spannungen der einzelnen Spannungsquellen überwachen und regeln, erfüllt werden.
Die Gesamtspannung von mehreren parallel geschalteten Spannungsquellen ist abhängig von den Quellenspannungen und den Innenwiderständen der einzelnen Spannungsquellen. Sie liegt in jedem Fall zwischen der niedrigsten und der höchsten Quellenspannung. Der Gesamtstrom ergibt sich aus der Summe der Ströme der einzelnen Quellen. Um den Innenwiderstand zu berechnen, sind die einzelnen Spannungsquellen zu Stromquellen zu transformieren (siehe weiter unten), der Widerstand kann dann als Parallelschaltung der einzelnen Innenwiderstände berechnet werden.
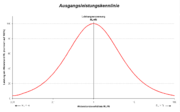
Leistung
Die von einer realen Spannungsquelle abgegebene Leistung berechnet sich aus dem Produkt des Stromes und der Klemmenspannung. Im Leerlauf beträgt diese Leistung Null, da kein Strom durch den Verbraucher fließt. Auch im Kurzschlussfall wird keine Leistung abgegeben, da zwar ein hoher Strom fließt, die Klemmenspannung aber gleich Null ist. Der Strom wird in diesem Fall allein durch den Innenwiderstand begrenzt, der die maximale von der Quelle lieferbare Leistung umsetzen muss.
Zwischen diesen beiden Extremen (Leerlauf und Kurzschluss) des Verbraucherwiderstandes gibt die Quelle eine Leistung ab, die größer als Null ist. Diese Leistung ist jedoch nicht konstant, sondern von Lastwiderstand abhängig. Somit gibt die Quelle für einen bestimmten Wert des Verbraucherwiderstands ein Maximum an Leistung ab. In diesem Fall spricht man von Leistungsanpassung. Dieser Fall tritt auf, wenn der Verbraucherwiderstand RV gleich dem Innenwiderstand Ri der Spannungsquelle ist: RV = Ri. Die maximale Leistung berechnet sich dann zu
Die Verlustleistung des Innenwiderstandes Ri
wird nahezu vollständig in Wärmeenergie umgewandelt. Sie ist also dafür mitverantwortlich, dass sich z. B. Batterien beim Entladen bzw. bei Akkumulatoren auch beim Laden, erwärmen. Bei einem Kurzschluss kann die vom Innenwiderstand umgesetzte Wärmeenergie die Spannungsquelle und in deren Nähe befindliche Gegenstände durch Hitze beschädigen, zerstören oder sie in Brand versetzen.
Transformation Spannungsquelle ↔ Stromquelle
Gemäß den Thévenin- und Norton-Theoremen lässt sich jede reale Spannungsquelle auch als eine reale Stromquelle ansehen. Welchen Begriff man verwendet, hängt davon ab, zu welcher Idealform das Verhalten der Quelle näher gesehen wird. Die nachfolgenden Gleichungen lassen sich ineinander umrechnen; die linke beschreibt die Stromquelle, die rechte die Spannungsquelle.
Literatur
- Paul A. Tipler: Physik. Spektrum Akademischer Verlag, Heidelberg 2000, ISBN 3-86025-122-8, Seite 758ff
Wikimedia Foundation.


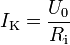
-Kennlinie_svg.png)