- Kontextfrei
-
Als Kontextfreie Sprache (engl. context-free languages, CFL) werden formale Sprachen bezeichnet, die über eine kontextfreie Grammatik verfügen, die diese Sprache erzeugt. Eine kontextfreie Grammatik erlaubt einen definierten Leseprozess (Interpretation) einer Sprache. Insbesondere bei Programmiersprachen kann dazu ein Parser verwendet werden. Kontextfreie Sprachen werden auch als Typ-2-Sprachen der Chomsky-Hierarchie bezeichnet.
Inhaltsverzeichnis
Charakterisierung
Die Klasse der kontextfreien Sprachen entspricht der Klasse der von nichtdeterministischen Kellerautomaten akzeptierten Sprachen. Die von deterministischen Kellerautomaten akzeptierten Sprachen werden als deterministisch kontextfreie Sprachen bezeichnet und sind identisch mit der Klasse der LR(k)-Sprachen (vgl. LR(k)-Grammatik).
Beispiele
Einfache Beispiele für kontextfreie Sprachen sind die Sprachen
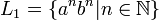 und
und 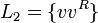 (Palindrome). Kontextfreie Sprachen finden in der Definition der Syntax von Programmiersprachen Anwendung, es lassen sich zum Beispiel arithmetische Ausdrücke und allgemein korrekte Klammerstrukturen festlegen. Grenzen der kontextfreien Sprachen liegen bei kontextrelevanten Eigenschaften, wie z. B. der Typüberprüfung in Programmiersprachen, die sich nur durch kontextsensitive Grammatiken darstellen lassen.
(Palindrome). Kontextfreie Sprachen finden in der Definition der Syntax von Programmiersprachen Anwendung, es lassen sich zum Beispiel arithmetische Ausdrücke und allgemein korrekte Klammerstrukturen festlegen. Grenzen der kontextfreien Sprachen liegen bei kontextrelevanten Eigenschaften, wie z. B. der Typüberprüfung in Programmiersprachen, die sich nur durch kontextsensitive Grammatiken darstellen lassen.Eigenschaften
Die Klasse der kontextfreien Sprachen ist abgeschlossen unter der
- Vereinigung
- Konstruktion: Seien G1 = (N1,T1,Π1,{S1}) und G2 = (N2,T2,Π2,{S2}) kontextfrei. Neues Startsymbol S und neue Produktion S:: = S1 | S2.
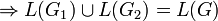 mit
mit 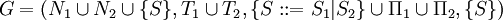
- Konstruktion: Seien G1 = (N1,T1,Π1,{S1}) und G2 = (N2,T2,Π2,{S2}) kontextfrei. Neues Startsymbol S und neue Produktion S:: = S1 | S2.
- Spiegelung
- Konkatenation (Verkettung)
- Konstruktion: Seien G1 = (N1,T1,Π1,{S1}) und G2 = (N2,T2,Π2,{S2}) kontextfrei. Neues Startsymbol S und neue Produktion S:: = S1S2.
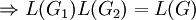 mit
mit 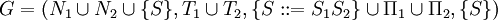
- Konstruktion: Seien G1 = (N1,T1,Π1,{S1}) und G2 = (N2,T2,Π2,{S2}) kontextfrei. Neues Startsymbol S und neue Produktion S:: = S1S2.
- Kleene-Stern
- Konstruktion: Sei G = (N,T,Π,{S}) kontextfrei. Neues Startsymbol Sneu und neue Produktion Sneu:: = SneuS.
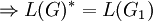 mit
mit 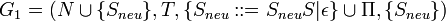
- Konstruktion: Sei G = (N,T,Π,{S}) kontextfrei. Neues Startsymbol Sneu und neue Produktion Sneu:: = SneuS.
- Anwendung von Homomorphismen
- Inverser Anwendung von inversen Homomorphismen
- Durchschnittbildung mit regulären Sprachen
Sie ist nicht abgeschlossen unter
- Durchschnitt
- Seien
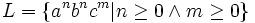 und
und 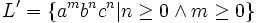 kontextfrei. Dann ist
kontextfrei. Dann ist 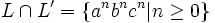 , jedoch nicht kontextfrei.
, jedoch nicht kontextfrei.
- Seien
- Komplement
- Seien L1,L2 kontextfrei und kontextfreie Sprachen unter Komplementbildung abgeschlossen. Dann sind auch
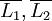 kontextfrei. Wegen der Abgeschlossenheit unter Vereinigung und De Morgan folgt, dass
kontextfrei. Wegen der Abgeschlossenheit unter Vereinigung und De Morgan folgt, dass 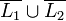 und damit
und damit 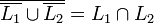 kontextfrei ist.
kontextfrei ist.
- Seien L1,L2 kontextfrei und kontextfreie Sprachen unter Komplementbildung abgeschlossen. Dann sind auch
- Anwendung von logarithmisch platzbeschränkter Reduktion
- Symmetrischer Differenz
Jede reguläre Sprache ist auch kontextfrei, da jede reguläre Grammatik auch eine kontextfreie Grammatik ist. Es existieren kontextsensitive Sprachen, die nicht kontextfrei sind. Durch das sogenannte Pumping-Lemma kann für eine Sprache gezeigt werden, dass sie nicht regulär bzw. kontextfrei ist.
Typische Entscheidungsprobleme
Seien L, L1 und L2 gegebene kontextfreie Sprachen über dem Alphabet Σ. Dann ergeben sich folgende typische Problemstellungen:
- Wortproblem: Gehört ein Wort
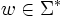 zu L?
zu L? - Leerheitsproblem: Ist L die leere Menge?
- Endlichkeitsproblem: Besteht L aus einer endlichen Menge von Wörtern (
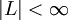 )?
)?
Die oben aufgezählten Probleme sind bei kontextfreien Sprachen entscheidbar. Das Äquivalenzproblem (L1 = L2) ist ab einschließlich dieser Stufe der Chomsky-Hierarchie nicht mehr entscheidbar.
Weitergehende Eigenschaften
- DLIN
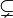 DCFL
DCFL 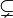 CFL
CFL 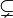 GCSL
GCSL 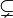 CSL
CSL - REG
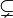 DLIN
DLIN 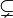 LIN
LIN 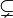 CFL
CFL - Für jedes
 gibt es Sprachen, die sich als Schnitt von n kontextfreien Sprachen darstellen lassen, aber nicht als Schnitt von n − 1 kontextfreien Sprachen.
gibt es Sprachen, die sich als Schnitt von n kontextfreien Sprachen darstellen lassen, aber nicht als Schnitt von n − 1 kontextfreien Sprachen.
Natürliche Sprache
In der Linguistik werden kontextfreie Grammatiken auch zur Beschreibung der Grammatik natürlicher Sprachen eingesetzt. Es wurde aber zum Beispiel für das Schweizerdeutsch nachgewiesen, dass die Sprache sich nicht vollständig mit einer solchen Grammatik beschreiben lässt.
Literatur
- Uwe Schöning: Theoretische Informatik kurzgefasst, 4. Auflage, Spektrum, ISBN 3827410991
- S.M. Shieber: Evidence against the context-freeness of natural language. In Linguistics and Philosophy 8, 333-343.
- John E. Hopcroft, Rajeev Motwani, Jeffrey Ullman: Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie. ISBN 3827370205
- Leonard Y. Liu und Peter Weiner: An Infinite Hierarchy of Intersections of Context-Free Languages. In: Mathematical Systems Theory 7, 185-192, 1973.
Siehe auch
- Backus-Naur-Form, eine kompakte formale Metasprache zur Darstellung kontextfreier Grammatiken.
- Vereinigung
Wikimedia Foundation.
