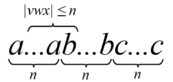Pumping-Lemma

Das Pumping-Lemma bzw. Pumplemma (auch Schleifensatz genannt) beschreibt in der theoretischen Informatik eine Eigenschaft bestimmter Klassen formaler Sprachen. In vielen Fällen lässt sich anhand des Lemmas nachweisen, dass eine formale Sprache nicht regulär bzw. nicht kontextfrei ist.

Seinen Namen hat das Lemma vom englischen Begriff to pump, zu deutsch aufpumpen. Es leitet sich davon ab, dass Teile von Wörtern aus Sprachen bestimmter Klassen vervielfacht (aufgepumpt) werden können, so dass die dabei entstehenden Wörter ebenfalls in der Sprache sind.

Man unterscheidet zunächst zwischen dem Pumping-Lemma für reguläre Sprachen und jenem für kontextfreie Sprachen. In der Literatur sind weiterhin Pumping-Lemmata für Erweiterungen der kontextfreien Sprachen anzutreffen. Mächtigere Sprachklassen in der Chomsky-Hierarchie wie die kontextsensitiven Sprachen und auch die wachsend kontextsensitiven Sprachen ermöglichen jedoch kein Pumpinglemma.

Alternativ wird das Lemma bzw. seine Ausprägungen auch als uvw-Theorem, uvwxy-Theorem, Schleifenlemma, Iterationslemma oder Lemma von Bar-Hillel bezeichnet.

Reguläre Sprachen

Pumping-Lemma für reguläre Sprachen

Für jede reguläre Sprache L gibt es eine natürliche Zahl n, so dass gilt: Jedes Wort z in L mit Mindestlänge n hat eine Zerlegung z = uvw mit den folgenden drei Eigenschaften:

1. Die beiden Wörter u und v haben zusammen höchstens die Länge n.
2. Das Wort v ist nicht leer.
3. Für jede nichtnegative Zahl i ist das Wort uvⁱw in der Sprache L. Das heißt die Wörter uw, uvw, uvvw, uvvvw, usw. sind alle in der Sprache L.

Neben den regulären Sprachen gibt es auch nicht-reguläre Sprachen, die dieses Lemma erfüllen. Eine notwendige und hinreichende Bedingung für reguläre Sprachen liefern der Satz von Myhill-Nerode oder Jaffes Pumping-Lemma.

Das Pumping-Lemma enthält mehrere Wechsel zwischen universeller und existentieller Quantifizierung. Diese kann man gut anhand der folgenden formalen Formulierung des Lemmas erkennen. Darin bezeichnet $\mathcal{L}_3$ die Menge aller regulärer Sprachen.

$\begin{align} \forall L \in \mathcal{L}_3.\, \exist n \in \mathbb{N}_0.\, \forall z \in L.\, |z|\ge n \implies \exist u, w, v.\ \ & z=u\cdot v\cdot w\ \land\\ &|uv| \leq n\ \land\\ &|v| > 0\ \land \\ &\forall i\in \mathbb{N}_0.\, u\cdot v^i\cdot w \in L \end{align}$

Beweis

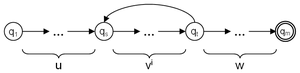
Die Gültigkeit des Lemmas basiert darauf, dass es zu jeder regulären Sprache einen deterministischen endlichen Automaten gibt, der die Sprache akzeptiert. Über einem endlichen Alphabet enthält eine reguläre Sprache mit unendlich vielen Wörtern auch solche Wörter, die mehr Zeichen enthalten als der Automat Zustände hat. Zum Akzeptieren solcher Wörter muss der Automat also einen Zyklus enthalten, der dann in beliebiger Häufigkeit durchlaufen werden kann. Die Buchstabenfolge, die beim Durchlaufen des Zyklus gelesen wird, kann also entsprechend beliebig oft in Wörtern der Sprache vorkommen.

Die Idee des Pumping-Lemmas ist, dass ein Wortteil durch einen Zyklus im deterministischen endlichen Automaten beliebig oft wiederholt werden kann.

Der folgende Beweis setzt die Mindestlänge n aus dem Lemma mit der Anzahl der Zustände des Automaten gleich und zeigt, dass wegen der Existenz eines Zyklus jedes Wort mit dieser Mindestlänge die geforderte Zerlegung besitzt.

Sei L eine reguläre Sprache. Ist L endlich, dann gibt es ein Wort mit maximaler Länge k. Sei n = k + 1, so ist für alle $z\in L$ die Prämisse $|z|\ge n$ falsch und die Implikation damit wahr.

Ist L unendlich, dann sei M ein deterministischer endlicher Automat, der L akzeptiert, und sei n die Anzahl der Zustände dieses Automaten. Da L regulär ist, existiert ein solcher Automat M immer.

Sei nun z ein beliebiges Wort aus L mit mindestens n Zeichen, also $\left|z\right| \geq n$. Bezeichne mit $q_1 \to \dots \to q_k$ die Zustandsfolge, die M beim Lesen von z beginnend mit dem Startzustand q₁ durchläuft. Insbesondere gilt k = | z | + 1. Da z in L ist, muss z von M akzeptiert werden, d.h. q_k muss ein Endzustand sein. Da der Automat M gerade n Zustände hat, muss spätestens nach dem Lesen von n Zeichen eine Zustandswiederholung eintreten. Das heißt es existieren $i \neq j \in \{1, \dots, n+1\}$ mit q_i = q_j. Der Automat M durchläuft auf z also einen Zyklus.

Sei v der Teil von z, der beim Durchlaufen des Zyklus $q_i \to \dots \to q_j$ gelesen wird. Ferner sei u der Teil von z, der beim Durchlaufen der davor liegenden Zustandsfolge $q_1 \to \dots \to q_i$ gelesen wird, und w sei der Teil von z, der beim Durchlaufen der dahinter liegenden Zustandsfolge $q_j \to \dots \to q_k$ gelesen wird. Mit dieser Wahl gilt z = uvw.

Mit dieser Wahl von u, v und w gelten die Aussagen aus dem Pumping-Lemma:

1. Die Länge von uv ist j − 1 und somit nicht größer als n.
2. Das Wort v ist nicht leer, da $i\neq j$ gilt, so dass beim Durchlauf des Zyklus mindestens ein Zeichen gelesen wird.
3. Für beliebiges $m \geq 0$ durchläuft der Automat beim Lesen des Worts uv^mw zunächst die Zustandsfolge $q_1 \to \dots \to q_i$, dann m-mal den Zyklus $q_i \to \dots \to q_j$ und schließlich die Zustandsfolge $q_j \to \dots \to q_k$. Am Ende befindet sich der Automat im Endzustand q_k. Somit gilt $uv^{m}w \in L$ für alle $m\geq 0$.

Beispiel

Ist die Sprache $L = \left\{a^mb^m \mid m \ge 1\right\}$ regulär?

Angenommen, L sei eine reguläre Sprache. Dann gibt es gemäß Pumping-Lemma eine Zahl n, so dass sich alle Wörter $z \in L$ mit $\left|z\right| \ge n$ wie beschrieben zerlegen lassen.

Man betrachte nun speziell das Wort z = uvw = aⁿbⁿ.

Gemäß Bedingung 1 ist v nicht leer, gemäß Bedingung 2 besteht uv und somit auch v ausschließlich aus as (da $\left|uv\right| \leq n$ und $\left|uvw\right| = \left|a^n b^n\right| = 2n$). Mit Bedingung 3 müsste das Wort $uv^2w = a^{n - \left|v\right|}a^{2 \cdot \left|v\right|}b^n = a^{n+ \left|v\right|}b^n$ in L liegen. Das ist aber offensichtlich falsch, denn dieses Wort hat mehr as als bs, da ${\left|v\right|}$ größer 0. Damit gilt: L kann nicht regulär sein.

Eine nicht-reguläre Sprache, die das Pumping-Lemma erfüllt

Die Sprache $L = \left\{a^mb^nc^n \mid m,n \ge 1\right\} \cup \{b^mc^n|m,n \ge 0 \}$ ist nicht regulär. Allerdings erfüllt L das Pumping-Lemma, denn jedes Wort $z \in L$ lässt sich so zerlegen z = uvw, dass auch für alle $i\ge0$ $uv^iw \in L$. Dazu kann v einfach als erster Buchstabe gewählt werden. Dieser ist entweder ein a, die Anzahl von führenden as ist beliebig. Oder er ist ein b oder c, ohne führende as ist aber die Anzahl von führenden bs oder cs beliebig.

Jaffes Pumping-Lemma

Jeffrey Jaffe hat ein verallgemeinertes Pumping-Lemma entwickelt ^[1], das äquivalent zur Definition der regulären Sprachen ist. Es ist also eine notwendige und hinreichende Bedingung zum Nachweis der Regularität einer Sprache.

Die Sprache $L \subseteq \Sigma ^{*}$ ist regulär genau dann, wenn eine Konstante $n > 0, n \in \mathbb{N}$ existiert, so dass es für alle $z \in \Sigma^{*}$, $|z| \ge n$ eine Zerteilung z = uvw mit $u, w \in \Sigma^{*}, v \in \Sigma^{+}$ gibt, so dass für alle $i \ge 0$ und Suffixe $x \in \Sigma^{*}$ gilt:

$zx \in L \iff uv^{i}wx \in L$.

Kontextfreie Sprachen

Annahmen

Sei $\mathcal{L}_2$ die Klasse aller Sprachen, die von Chomsky-Hierarchie-Typ-2-Grammatiken erzeugt werden. $\mathcal{L}_2$ bezeichnet somit die Klasse der kontextfreien Sprachen.

Aussage des Pumping-Lemmas für kontextfreie Sprachen

Für eine kontextfreie Sprache L gibt es eine natürliche Zahl n so, dass sich alle Wörter z der Sprache mit Mindestlänge n in fünf Teilworte uvwxy zerlegen lassen, wobei das zweite und das vierte Wort vx nicht beide leer sein dürfen, die drei mittleren Worte zusammen vwx nicht länger als n sind, und das zweite und vierte beliebig, aber gleich oft (auch keinmal) wiederholt werden dürfen, ohne dass das entstehende, aufgepumpte Wort nicht mehr in der Sprache L wäre:

$\begin{align} \forall L \in \mathcal{L}_2.\, \exist n \in \mathbb{N}_0.\, \forall z \in L.\, |z|\ge n \implies \exist u,v,w,x,y.\ \ & z=u\cdot v\cdot w\cdot x\cdot y\ \land\\ &|vwx| \leq n\ \land\\ &|vx| > 0\ \land \\ &\forall i\in \mathbb{N}_0.\, u\cdot v^i\cdot w\cdot x^i\cdot y \in L \end{align}$

Neben den kontextfreien Sprachen gibt es auch nicht kontextfreie Sprachen, die dieses Pumping-Lemma erfüllen. Die Umkehrung des Lemmas gilt im Allgemeinen also nicht. Eine Verallgemeinerung des Pumping-Lemmas für kontextfreie Sprachen ist Ogdens Lemma.

Korrektheitsbeweis

Gegeben sei eine kontextfreie Grammatik G in Chomsky-Normalform mit N Variablen, für die gilt, dass sie gerade die gewünschte Sprache beschreibt. Sei nun ein Wort x aus dieser Sprache gegeben, für das gilt: $\left|x\right| \geq 2^{\left|N\right|} = n$.

Die Idee des Pumping-Lemmas für kontextfreie Sprachen ist, dass ein Wortteil durch mehrfaches Ableiten derselben Variablen beliebig oft wiederholt werden kann.

Betrachten wir nun einen Ableitungsbaum T für x mit Höhe h. Da unsere Sprache in CNF angegeben wurde, hat T die Form eines Binärbaumes. Daraus folgt für die Höhe von T $h \geq \log(n) = \left|N\right|$. Es gibt also einen Pfad $v_0 \ldots v_h$ in T von der Wurzel zu einem Blatt, für den gilt, dass er Länge $h+1 > \left|N\right|$ hat. 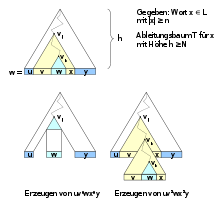Es existieren also zwei Knoten v_j,v_k auf diesem Pfad mit $0 \leq j < k \leq h$, welche die gleichen Variablen von G A_j,A_k repräsentieren.

Betrachtet man den Teilbaum T_k, welcher von v_k aus aufgespannt wird, so bilden dessen Blätter den Teilstring w. Der Teilbaum T_j, welcher von v_j aufgespannt wird, besitzt als Teilbaum den Baum T_k. Man kann also die Blätter von T_j aufteilen in Blätter links von T_k und Blätter rechts von T_k und erhält somit eine Aufteilung der Blätter von T_j der Form vwx. Ebenso unterteilt der Teilbaum T_j den gesamten Ableitungsbaum in drei Teile u,vwx,y. Wir erhalten also als Aufteilung die Teilstrings u,y, welche im Ableitungsbaum links bzw. rechts von dem von v_j aufgespannten Teilbaum liegen, die Teilstrings v,x, welche in dem Teilbaum T_j liegen nicht jedoch in T_k, und zu guter Letzt den Teilstring w, welcher in T_k liegt. Da v_j und v_k die gleichen Variablen unserer Grammatik repräsentieren, folgt daraus, dass der Pfad von v_j nach v_k beliebig oft wiederholt werden kann. Durch eine Wiederholung des Pfades würden wir Worte der Form uvⁱwxⁱy erzeugen, ohne unsere Sprache zu verlassen. Womit wir das Pumping-Lemma für kontextfreie Sprachen bewiesen hätten.

Beispiel

Das Wort vwx enthält höchstens zwei verschiedene Buchstaben.

Ist die Sprache $L = \left\{ a^mb^mc^m \mid m \ge 1\right\}$ kontextfrei?

Wir nehmen an, L sei kontextfrei. Sei dann n die zugehörige Konstante aus dem Pumping-Lemma.

Wir betrachten das Wort z = aⁿbⁿcⁿ. Es muss dann eine Zerlegung z = uvwxy geben, so dass $\left| vx \right| \ge 1$, $\left| vwx \right| \le n$, $uv^iwx^iy \in L$ für alle $i \ge 0$ ist. Da $\left| vwx \right| \le n$, enthält das Wort vwx höchstens zwei verschiedene Buchstaben. Da $\left| vx \right| \ge 1$, kann uv²wx²y nicht von allen drei Buchstaben gleich viele enthalten. Also kann L nicht kontextfrei sein.

Quellen

1. ↑ Jeffrey Jaffe: A necessary and sufficient pumping lemma for regular languages