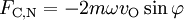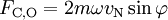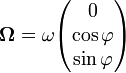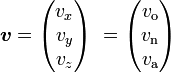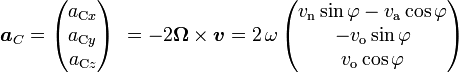- Korioliskraft
-
Die Corioliskraft gehört zu den Schein- oder Trägheitskräften. Sie wirkt auf jeden Körper, dessen Bewegung in einem rotierenden Bezugssystem beschrieben wird. Benannt ist sie nach Gaspard Gustave de Coriolis, der sie 1835 erstmals mathematisch herleitete.
Die Richtung der Corioliskraft ist senkrecht sowohl zur Bewegungsrichtung des Körpers als auch zur Rotationsachse des Bezugssystems. Ihr Betrag ist proportional zur Masse des bewegten Körpers, zur Rotationsfrequenz und zur Projektion des Geschwindigkeitsvektors auf die Ebene senkrecht zur Rotationsachse. Sind Bewegungsrichtung und Rotationsachse parallel, ist sie Null.
In der Meteorologie und der physikalischen Ozeanographie spielt die Corioliskraft eine wichtige Rolle. Aufgrund der Erdrotation bewegen sich die Luft- und Wassermassen in einem rotierenden Bezugssystem. Dies bewirkt auf der Nordhalbkugel eine Ablenkung nach rechts, was die Drehrichtung von Hoch- und Tiefdruckgebieten bestimmt.
Inhaltsverzeichnis
Einführung – Die Corioliskraft auf einem Drehteller
Eine Person auf einer sich drehenden Scheibe (z. B. einem Karussell) spürt eine nach außen gerichtete Zentrifugalkraft. Bewegt sie sich außerdem auf der Scheibe, so spürt sie darüber hinaus eine zur Seite gerichtete Kraft. Dies ist die Corioliskraft.
Es ist ein verbreitetes Missverständnis, dass die Corioliskraft nur bei radialen Bewegungen, also bei solchen, die entweder vom Mittelpunkt weg oder zu ihm hin gerichtet sind, wirkt. Tatsächlich wirkt sie bei beliebigen horizontalen Bewegungen auf der Drehscheibe, steht jeweils senkrecht auf der Bewegungsrichtung und hat jeweils den gleichen Betrag. Dreht sich die Scheibe im Uhrzeigersinn, wirkt die Corioliskraft aus Sicht der sich bewegenden Person nach links. Bei einer Drehung gegen den Uhrzeigersinn wirkt sie nach rechts.
Corioliskraft in der Technik
Corioliskräfte sind in der Technik dann von Bedeutung, wenn eine Drehbewegung mit einer zweiten Bewegung „überlagert“ wird. Dies ist beispielsweise in einem Roboter der Fall, der sich dreht und gleichzeitig seinen Greifarm ausfährt.
- Wenn eine Last an einem Kran nach innen oder außen fährt, während der Kran sich dreht, hängt sie aufgrund der Corioliskraft nicht senkrecht nach unten, sondern wird seitlich abgelenkt. Wird die Last längs des Krans nach innen eingefahren, eilt sie – entgegen der Intuition – dem Kran voraus.
- In der Getriebetechnik (Koppelgetriebe) und in der Robotik spielen die Corioliskräfte ebenfalls eine wichtige Rolle, da auch hier gleichzeitige Bewegungen entlang mehrerer Freiheitsgrade erfolgen. Benutzt man zur Vereinfachung der Beschreibung rotierende Koordinatensysteme, treten für Bewegungen in diesen rotierenden Bezugssystemen auch Corioliskräfte auf.
- Zur Messung des Massenstromes durchströmender Flüssigkeiten oder Gase verwendet man den Coriolis-Massendurchflussmesser, dessen Funktionsweise auf der Corioliskraft beruht.
Corioliskraft in der Raumfahrt
 Trojanerasteroiden auf den Librationspunkten von Jupiter. Aufgrund der Corioliskraft umkreisen sie auf einem Halo-Orbit diese Punkte.
Trojanerasteroiden auf den Librationspunkten von Jupiter. Aufgrund der Corioliskraft umkreisen sie auf einem Halo-Orbit diese Punkte.Der Flug einer Raumsonde zu einem anderen Planeten des Sonnensystems kann näherungsweise durch das astronomische Dreikörperproblem beschrieben werden. Die relevanten drei Körper sind die Sonne, der Zielplanet und die Raumsonde. Beschreibt man die Bewegung der Raumsonde in einem rotierenden Koordinatensystem, in welchem die Sonne und der Zielplanet ruhen, wirkt auf die Raumsonde die Corioliskraft. Bei der Berechnung der Bahn der Raumsonde muss diese neben den Gravitationskräften von Sonne und Planet berücksichtigt werden. Das Sonnenteleskop SOHO nutzt diesen Effekt positiv aus und umkreist einen Librationspunkt zwischen Erde und Sonne. Einen solchen Orbit nennt man Halo-Orbit.
Corioliskraft auf der Erde
Auf jedes sich auf der Erde bewegende Objekt wirkt eine Corioliskraft, die auf die Erdrotation zurückgeht. Der Einfluss der Erdrotation auf die Bewegung von Körpern wurde erstmals von Isaac Newton untersucht.
Vertikale Bewegungen
Bei Abwärtsbewegung (senkrecht zur Erdoberfläche) ist die Corioliskraft nach Osten gerichtet, bei Aufwärtsbewegung nach Westen.
Lässt man einen Gegenstand fallen, wird er aufgrund der Corioliskraft nach Osten abgelenkt. Frühe Messungen dieses Effektes stammen von Giovanni Battista Guglielmini (1791 in Bologna), Johann Friedrich Benzenberg (1802 in Hamburg) und Ferdinand Reich (1832 in Freiberg), siehe Fallexperimente zum Nachweis der Erdrotation.
Marin Mersenne schreibt man zu, die Frage aufgeworfen zu haben, wo – ohne Berücksichtigung von Luftbewegung und Luftwiderstand – eine senkrecht nach oben geschossene Kanonenkugel zu Boden fällt. Durch die Corioliskraft wird sie während der Aufwärtsbewegung nach Westen und während der Abwärtsbewegung nach Osten beschleunigt. Ihr Geschwindigkeitsvektor erlangt daher eine horizontale Komponente, die während des gesamten Fluges nach Westen gerichtet ist und im Umkehrpunkt ihr Maximum erreicht. Im Ergebnis wird sie daher nach Westen abgelenkt. Bei einer Anfangsgeschwindigkeit von 100 m/s und einer geographischen Breite von 50° beträgt die Westablenkung beispielsweise 65 cm.
 Gleichgewicht zwischen der Corioliskraft und dem Druckgradienten am Beispiel eines Tiefdruckgebietes auf der Nordhalbkugel.
Gleichgewicht zwischen der Corioliskraft und dem Druckgradienten am Beispiel eines Tiefdruckgebietes auf der Nordhalbkugel.
Rot – horizontale Komponente der Corioliskraft
Blau – DruckgradientkraftHorizontale Bewegungen
Bei horizontalen Bewegungen auf der Erde hat die Corioliskraft eine horizontale und eine vertikale Komponente.
Die vertikale Komponente ist klein gegenüber der Schwerkraft. Ein am Äquator mit Schallgeschwindigkeit nach Osten fliegendes Flugzeug wird beispielsweise durch die Vertikalkomponente der Corioliskraft um annähernd ein Tausendstel seines Gewichts leichter - fliegt es nach Westen, wird es entsprechend schwerer. Die vertikale Komponente der Corioliskraft auf der Erde spielt in der Praxis nur als Korrekturglied bei Präzisionsmessungen des Erdschwerefeldes eine Rolle.
Auf der Erde bezeichnet man daher meist die horizontale Komponente als „die Corioliskraft“. Die horizontale Komponente zieht den bewegten Beobachter auf der Nordhalbkugel nach rechts und auf der Südhalbkugel nach links, und zwar umso stärker, je näher er sich an den Polen befindet. Bei Bewegungen am Äquator ist die horizontale Komponente der Corioliskraft Null. Der Betrag der horizontalen Komponente hängt nicht von der Richtung der Bewegung ab. Bei einer Nord-Süd-Bewegung wirkt exakt die gleiche horizontale Komponente der Corioliskraft wie bei einer Ost-West-Bewegung.
Die Corioliskraft hat wesentlichen Einfluss auf die Formen der großräumigen Bewegungen in der Atmosphäre und im Ozean. Erstmals theoretisch berücksichtigt wurde sie diesbezüglich in der von Laplace (1778) aufgestellten Gezeitentheorie. Der Einfluss der Corioliskraft auf Bewegungen etwa im Meer und in der Atmosphäre wird durch die dimensionslose Rossby-Zahl charakterisiert, je kleiner diese ist, umso mehr Einfluss hat die Corioliskraft auf die Bewegung.
Einfluss der Corioliskraft auf das Wetter
 Auswirkung der Corioliskraft auf ein großskaliges Windsystem, hier Tiefdruckgebiet bei Island (Nordhalbkugel)
Auswirkung der Corioliskraft auf ein großskaliges Windsystem, hier Tiefdruckgebiet bei Island (Nordhalbkugel)Die Corioliskraft ist dafür verantwortlich, dass sich die Luftmassen um großräumige Hochdruckgebiete auf der Nordhalbkugel im Uhrzeigersinn, um Tiefdruckgebiete im Gegenuhrzeigersinn bewegen. Bei einem Tiefdruckgebiet strömt die Luft aufgrund des Druckgefälles nach innen. Diese Strömung wird auf der Nordhalbkugel durch die Corioliskraft nach rechts abgelenkt und es ergibt sich eine gegen den Uhrzeigersinn gerichtete Rotation. Das sich ergebende Strömungsbild lässt sich auch durch das geostrophische Gleichgewicht zwischen dem horizontalen Druckgradienten und der Corioliskraft erklären: Auf einen Wirbel, der sich gegen den Uhrzeigersinn dreht, wirkt die Corioliskraft nach außen und kompensiert die nach innen gerichtete Kraft des Druckgefälles. Allgemein dreht sich die Luft auf der Nordhalbkugel um Tiefdruckgebiete immer gegen den Uhrzeigersinn und um Hochdruckgebiete im Uhrzeigersinn. Auf der Südhalbkugel ist dies genau umgekehrt. Das geostrophische Gleichgewicht formt nur die großskaligen Wettermuster. Auf die Drehrichtung beispielsweise von Tornados hat die Corioliskraft keinen direkten Einfluss. Weiterhin spielt die Corioliskraft auch bei der Bildung der Rossbywellen und Yanai-Wellen eine wichtige Rolle.
Corioliskraft und Eisenbahn
Im Schienenverkehr führt die Corioliskraft auf der Nordhalbkugel dazu, dass bei geraden Strecken diejenige Schiene, die in Fahrtrichtung rechts liegt, geringfügig stärker belastet wird als die linke Schiene. Ein Zug (z. B. ein ICE 3 mit 400 t Masse), der bei einer geografischen Breite von 51 Grad (Köln) mit einer Geschwindigkeit von 250 km/h fährt, erfährt eine Kraft von 3.200 N nach rechts. Hat der Zug acht Wagen mit je vier Achsen, wird jedes rechte Rad mit einer Corioliskraft von ca. 100 N nach rechts gegen die Schiene gedrückt. Dies entspricht etwa einem Promille der Normalkraft. Im Vergleich dazu ergibt sich bei dieser Geschwindigkeit bei einem Kurvenradius von 3.000 m auf jedes Rad eine seitliche Kraft von 20.000 N, also 200 mal mehr als die Corioliskraft.
Trägheitskreise
Aufgrund der Corioliskraft beschreibt eine Luft- oder Wassermasse, die sich in einem mit der Erde mitrotierenden Bezugssystem mit der Geschwindigkeit
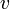 bewegt ohne Einfluss anderer Kräfte „Trägheitskreise“ mit Radien von
bewegt ohne Einfluss anderer Kräfte „Trägheitskreise“ mit Radien von 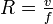 . In mittleren Breiten mit Werten des Coriolisparameters (siehe unten) von
. In mittleren Breiten mit Werten des Coriolisparameters (siehe unten) von 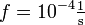 und einer typischen Meeres-Strömungsgeschwindigkeit von
und einer typischen Meeres-Strömungsgeschwindigkeit von 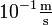 ergibt sich ein Radius von
ergibt sich ein Radius von 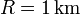 . Die Bewegung erfolgt auf der Nordhalbkugel im Uhrzeigersinn, auf der Südhalbkugel entgegen dem Uhrzeigersinn. Die Periode der Umlaufbewegung ist
. Die Bewegung erfolgt auf der Nordhalbkugel im Uhrzeigersinn, auf der Südhalbkugel entgegen dem Uhrzeigersinn. Die Periode der Umlaufbewegung ist 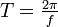 , z. B. bei 60 Grad geographischer Breite rund 15 Stunden. Sie wurden z. B. bei frei schwimmenden Bojen in der Ostsee beobachtet, die zunächst einer durch starke Winde angefachten Oberflächenströmung folgten, nach dem Abflauen des Windes aber Kreisbahnen bzw. Zykloiden (da eine Strömung der Kreisbewegung überlagert war) beschrieben.[1] Für den Verlauf von Meeres- und Luftströmungen spielt die Corioliskraft eine wichtige Rolle, neben anderen Kräften, die sich mit ihr ins Gleichgewicht setzen oder sie sogar dominieren (Geostrophie).
, z. B. bei 60 Grad geographischer Breite rund 15 Stunden. Sie wurden z. B. bei frei schwimmenden Bojen in der Ostsee beobachtet, die zunächst einer durch starke Winde angefachten Oberflächenströmung folgten, nach dem Abflauen des Windes aber Kreisbahnen bzw. Zykloiden (da eine Strömung der Kreisbewegung überlagert war) beschrieben.[1] Für den Verlauf von Meeres- und Luftströmungen spielt die Corioliskraft eine wichtige Rolle, neben anderen Kräften, die sich mit ihr ins Gleichgewicht setzen oder sie sogar dominieren (Geostrophie).Corioliskraft und Foucaultsches Pendel
Der Begriff der Corioliskraft erlaubt ein einfaches Verständnis des Foucaultschen Pendels. Da das Pendel (auf der Nordhalbkugel) durch die Corioliskraft nach rechts gezogen wird, dreht sich seine Schwingungsebene. Die Geschwindigkeit der Drehung nimmt mit zunehmendem Abstand vom Pol ab.
Erosion von Flussufern
Die Corioliskraft führt auch dazu, dass auf der Nordhalbkugel die Flussufer, welche in Fließrichtung rechts liegen, im Mittel stärker erodiert werden als die linken. Dieses Phänomen wurde erstmals im Jahre 1763 von Michail Wassiljewitsch Lomonossow beschrieben. Erste Erklärungen stammten von P. A. Slowzow (1827) und Karl Ernst von Baer (1856)[2]. Obwohl diese Forscher glaubten, der Effekt trete nur bei Flüssen auf, die von Süden nach Norden fließen, wird der Effekt bis heute als Baersches Gesetz bezeichnet. Die korrekte Sichtweise, dass der Effekt von der Fließrichtung unabhängig ist, formulierte 1859 erstmals Jacques Babinet und später Albert Einstein[3] (1926).[4]
Einfluss der Corioliskraft auf den Wasserabfluss in einem Becken
Eine oft anzutreffende Meinung bezüglich der Corioliskraft bezieht sich auf das Drehverhalten eines Wasserstrudels, zum Beispiel in einer Badewanne. Wird der Abfluss geöffnet, soll sich der entstehende Strudel auf der Nordhalbkugel gegen den Uhrzeigersinn bewegen, auf der Südhalbkugel entsprechend mit dem Uhrzeigersinn – ähnlich wie die Tiefdruckgebiete der Atmosphäre. Tatsächlich spielt die Corioliskraft in solch kleinen Dimensionen keine praktische Rolle. Im Vergleich zu anderen Einflüssen, beispielsweise bereits existenten Strömungen, ist der Einfluss der Corioliskraft vernachlässigbar.
Formeln
Die Corioliskraft
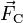 ist ebenso wie die Zentrifugalkraft ein Teil der Trägheitskraft, die auf einen sich in einem rotierenden Bezugssystem bewegenden Körper wirkt.
ist ebenso wie die Zentrifugalkraft ein Teil der Trägheitskraft, die auf einen sich in einem rotierenden Bezugssystem bewegenden Körper wirkt.Allgemein gilt
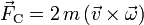 ,
,
wobei
- m die Masse des bewegten Körpers,
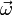 der Winkelgeschwindigkeitsvektor der Rotation
der Winkelgeschwindigkeitsvektor der Rotation- und
 der Geschwindigkeitsvektor der Bewegung des Körpers, relativ zum rotierenden Bezugssystem, ist.
der Geschwindigkeitsvektor der Bewegung des Körpers, relativ zum rotierenden Bezugssystem, ist.
Im Fall der Erdrotation (eine Umdrehung in 24 Stunden) ist die Winkelgeschwindigkeit
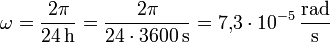 .
.Horizontale Bewegungen
Betrachtet man die Corioliskraft aufgrund der Erdrotation, interessiert man sich meist nur für horizontale Bewegungen und auch nur für die horizontale Komponente der Corioliskraft.
Für diese gilt:
bzw.
Dabei ist
- FC,N die Komponente der Corioliskraft in nördlicher Richtung,
- FC,O die Komponente der Corioliskraft in östlicher Richtung,
 der Breitengrad,
der Breitengrad,- vO die Komponente des Geschwindigkeitsvektors in östlicher Richtung
- und vN die Komponente des Geschwindigkeitsvektors in nördlicher Richtung.
Vertikale Bewegungen
Bei reinen Aufwärtsbewegungen wirkt die Corioliskraft nach Westen, beim senkrechten freien Fall wirkt sie nach Osten. Ihr Betrag ist
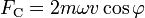 .
.
Ein über die Länge L frei fallender Körper erfährt aufgrund der Corioliskraft eine Ostablenkung von
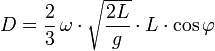 .
.
Eine mit der Anfangsgeschwindigkeit v0 senkrecht nach oben geschossene Kugel fällt aufgrund der Corioliskraft westlich vom Abschusspunkt auf die Erde, und zwar mit einem Versatz von
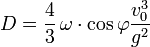 .
.
g ist dabei jeweils die Erdschwerebeschleunigung.
Am Äquator ist der Versatz am größten (
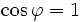 ). Wegen
). Wegen 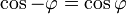 ergibt sich kein Unterschied auf der Nord- oder Südhalbkugel.
ergibt sich kein Unterschied auf der Nord- oder Südhalbkugel.Gesamtbetrachtung der Corioliskomponenten auf einer rotierenden Kugel
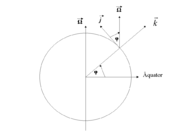
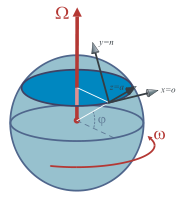
Man betrachte einen Ort auf der Breite φ einer Kugel, die um die Nord-Süd-Achse rotiert. Dann gibt es ein lokales, kartesisches Koordinatensystem, wobei dessen x-Achse horizontal nach Osten zeigt, die y-Achse horizontal nach Norden und die z-Achse vertikal nach oben (aufwärts). Der Rotationsvektor Ω, der Geschwindigkeitsvektor v und die Coriolisbeschleunigung aC können in diesem lokalen Koordinatensystem beschreiben werden als:
wobei folgende Indizes gelten:
- Osten: o
- Norden: n
- Aufwärts: a
Verwandte Begriffe
Mit der Coriolisbeschleunigung aC wird ein Körper in Richtung der Corioliskraft beschleunigt, wenn dieser keine andere Kraft entgegenwirkt. Der Betrag der Coriolisbeschleunigung ist dann aC = FC / m, wobei m die Masse des Körpers ist.
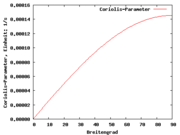
Mit dem Coriolisparameter
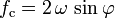 kann man die Formeln für die horizontale Komponente der Corioliskraft aufgrund der Erdrotation einfacher darstellen. Der Betrag der Corioliskraft ist dann einfach FC = fcmv. Typische Größenordnung in mittleren Breiten sind Werte von fc von um
kann man die Formeln für die horizontale Komponente der Corioliskraft aufgrund der Erdrotation einfacher darstellen. Der Betrag der Corioliskraft ist dann einfach FC = fcmv. Typische Größenordnung in mittleren Breiten sind Werte von fc von um 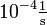 .
.Als Corioliseffekt bezeichnet man jede Erscheinung, die durch die Corioliskraft zustande kommt.
Quellen
- J. F. Benzenberg: Versuche über das Gesetz des Falles, den Widerstand der Luft und die Umdrehung der Erde. Dortmund 1804, 2. Auflage Hamburg 1824
- F. Reich: Fallversuche über die Umdrehung der Erde: angestellt in dem Brüderschachte bei Freiberge.Freiberg 1832
- G. Coriolis: Memoire sur les equations du mouvement relatifs des systems de corps. In: J. Ec. Polytech.. Nr. 15, 1835, S. 142–154 (http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/Coriolis-1835.pdf).
- Adrian Gill: Atmosphere-Ocean Dynamics (International Geophysics). Academic Pr Inc, 1982, ISBN 0122835220.
- P. S. Laplace: Recherches sur plusieurs points du système du monde. In: Mém. Acad. Roy. d. Sci.. 88, 1775, S. 75-182 (http://mathdoc.emath.fr/cgi-bin/oetoc?id=OE_LAPLACE__9).
Zu dieser Quelle sollte man die Fußnote 12 in „The Coriolis Effect: Four centuries of conflict between common sense and mathematics“[5] beachten - K. E. von Baer: 'Über ein allgemeines Gesetz in der Gestaltung der Flußbetten. In:Kaspische Studien. Nr. VIII, 1860, S. 1–6.
Einzelnachweise
- ↑ Anders Persson The Coriolis Effect, englisch, pdf Datei
- ↑ L. S. Berg: P. A. Slowzow und das Baersche Gesetz. In: Geschichte der russischen geographischen Entdeckungen. Gesammelte Aufsätze. VEB. Bibliographisches Institut, Leipzig. 1954.
- ↑ A. Einstein: Die Ursache der Mäanderbildung der Flußläufe und des sogenannten Baerschen Gesetzes. In: Die Naturwissenschaften. 14, Nr. 11, 1926, S. 223-224.
- ↑ Peeter Müürsepp: Über die Wirkung der Corioliskraft auf die Erosion von Flussufern. (wissenschaftshistorische Abhandlung)
- ↑ A. O. Persson: The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885. In: History of Meteorology. 2, 2005, S. 1 ([1]).
Links
Wikimedia Foundation.