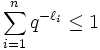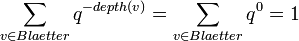- Kraftsche Ungleichung
-
Sei T ein (n,q)-Baum mit maximal q Kindknoten je Knoten und n Blättern, deren Tiefen
 seien.
seien.Dann gilt:
Gleichheit gilt, falls T ein vollständiger Baum ist.
Beweis
Man sieht leicht, dass für einen Baum der Tiefe 0 gilt:
Da ein Knoten eines q-nären Baumes maximal q Kinder hat oder ein Blatt ist, verteilt jeder Knoten seinen Wert q − k (Tiefe k) auf maximal q Kinder mit dem Wert q − (k + 1), die zusammen höchsten einen Wert von
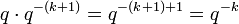 besitzen. Ist der Baum unvollständig, dh. besitzt ein Knoten weniger als k Kinder, so sinkt die Summe sogar unter 1. Die Ungleichung wird genau dann verletzt, wenn innere Knoten als Blätter verwendet werden, weil zB. alle Knoten auf einer Tiefenebene als Codewort verwendet werden, gleichzeitig aber noch längere, tiefer liegendere Codewörter existieren. Da diese längeren Codewörter dann aber ein Codewort als Präfix haben, ist dadurch auch die Eigenschaft der Präfixfreiheit verletzt. Es ist natürlich möglich und auch nicht selten, dass der Baum unbalanciert ist, dh. ein Pfad mit der Länge
besitzen. Ist der Baum unvollständig, dh. besitzt ein Knoten weniger als k Kinder, so sinkt die Summe sogar unter 1. Die Ungleichung wird genau dann verletzt, wenn innere Knoten als Blätter verwendet werden, weil zB. alle Knoten auf einer Tiefenebene als Codewort verwendet werden, gleichzeitig aber noch längere, tiefer liegendere Codewörter existieren. Da diese längeren Codewörter dann aber ein Codewort als Präfix haben, ist dadurch auch die Eigenschaft der Präfixfreiheit verletzt. Es ist natürlich möglich und auch nicht selten, dass der Baum unbalanciert ist, dh. ein Pfad mit der Länge 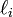 existiert, während in einem anderen Ast noch tiefer liegendere Blätter zu finden sind. Andererseits ist es aber auch möglich, "dumme" Codes zu konstruieren, die die Ungleichung erfüllen, aber trotzdem einen Teil eines Pfades zu einem Blatt als Codewort verwenden.
existiert, während in einem anderen Ast noch tiefer liegendere Blätter zu finden sind. Andererseits ist es aber auch möglich, "dumme" Codes zu konstruieren, die die Ungleichung erfüllen, aber trotzdem einen Teil eines Pfades zu einem Blatt als Codewort verwenden.Im Kontext der Codierungstheorie müssen für jeden eindeutig dekodierbaren Code C über dem Alphabet der Länge q die Längen der Codeworte
 die Kraft-Ungleichung erfüllen. In der Umkehrung existiert zu jeder Menge von Codewort-Längen, welche die Kraft-Ungleichung erfüllt, ein eindeutig dekodierbarer, präfixfreier Code mit diesen Längen.
die Kraft-Ungleichung erfüllen. In der Umkehrung existiert zu jeder Menge von Codewort-Längen, welche die Kraft-Ungleichung erfüllt, ein eindeutig dekodierbarer, präfixfreier Code mit diesen Längen.Beweis für unendliche Folgen von Codewortlängen
Sei
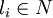 für alle
für alle 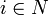
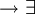 genau dann ein präfixfreier Binärcode, wenn
genau dann ein präfixfreier Binärcode, wenn 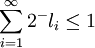
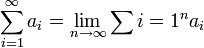
"
 "
"- Seien
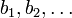 präfixfreie Binärcode mit Codewortlängen
präfixfreie Binärcode mit Codewortlängen 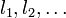
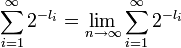 . Da
. Da 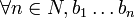 endlicher präfixfreier Binärcode, gilt weiter für
endlicher präfixfreier Binärcode, gilt weiter für 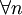
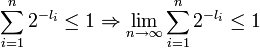
"
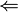 "
"- Sei
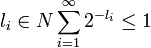
Die Summe konvergiert absolut
 wir können umsortieren
wir können umsortieren  o.B.d.A
o.B.d.A 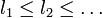
- Induktion nach k
- k = 1 OK
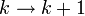 haben präfixfreien Binärcode
haben präfixfreien Binärcode 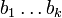 zu
zu 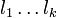 , repräsentiere B als Binärbaum D und ersetze dann jedes Blatt der aktuellen Tiefe durch vollständigen Binärbaum der Höhe lk + 1 − l + 1. Das ändert nichts an der "Hinzufügbarkeit", alle Blätter in D' haben Tiefe lk + 1 und an der Summe ändert sich auch nichts, denn
, repräsentiere B als Binärbaum D und ersetze dann jedes Blatt der aktuellen Tiefe durch vollständigen Binärbaum der Höhe lk + 1 − l + 1. Das ändert nichts an der "Hinzufügbarkeit", alle Blätter in D' haben Tiefe lk + 1 und an der Summe ändert sich auch nichts, denn 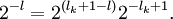
Sei b gleich der Anzahl der Blätter in T
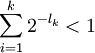 . Dann gilt
. Dann gilt 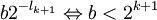
 T' nicht vollständig
T' nicht vollständig  Können Codewort mit Länge lk + 1 hinzufügen
Können Codewort mit Länge lk + 1 hinzufügen  def. b induktiv, daraus ergibt sich präfixfreier Binärcode.
def. b induktiv, daraus ergibt sich präfixfreier Binärcode.Literatur
- Leon G. Kraft; MS Thesis, Electrical Engineering Department, Massachusetts Institute of Technology (Hrsg.): A device for quantizing, grouping, and coding amplitude modulated pulses. Cambridge, MA 1949 (http://dspace.mit.edu/handle/1721.1/12390).
- B. McMillan: Two inequalities implied by unique decipherability. In: IEEE Trans. Information Theory. 2, Nr. 4, 1956, S. 115–116 (http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1056818).
Wikimedia Foundation.