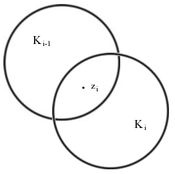
Kreiskette

Veranschaulichung

In der Mathematik und da besonders in der Funktionentheorie wird eine Menge von Kreisscheiben $(K_0, \dots, K_n)$ in der komplexen Ebene Kreiskette genannt, wenn die Kreisscheiben offen nicht disjunkt sind. Sie bilden dann eine Zusammenhangskomponente und sind ein wichtiges Hilfsmittel, um holomorphe Funktionen, die nur auf der ersten Kreisscheibe K₀ definiert ist, analytisch fortzusetzen.

Definition

Seien $K_0,\ldots,K_n \subset \C$ offene Kreisscheiben. Ihre Vereinigung ist eine Kreiskette, wenn für alle j < n ein $z_j \in K_j\cap K_{j+1}$ existiert, der Schnitt zweier aufeinanderfolgender Kreisscheiben also nicht leer ist.

Literatur

• Klaus Jänich: Funktionentheorie. 6 Auflage. Springer, 2004, ISBN 3540203923, S. 46-60.