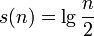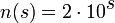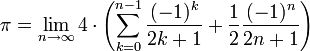- Kreiszahlberechnung nach Leibniz
-
Im Jahre 1682 steuerte Gottfried Wilhelm Leibniz der Suche nach einer bestmöglichen Annäherung an die Kreiszahl Pi folgende Formel bei, die auch als Leibniz-Reihe bekannt ist:
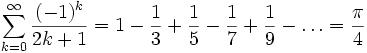 .
.
Dabei erhöht sich der Wert des Nenners eines jeden Summanden im Vergleich zum vorherigen um jeweils 2. Diese Formel war dem indischen Mathematiker Madhava bereits im 14. Jahrhundert und dem schottischen Mathematiker Gregory vor 1671 bekannt, Leibniz entdeckte sie für die kontinentaleuropäische Mathematik neu.
Die Konvergenz dieser unendlichen Reihe folgt unmittelbar aus dem Leibniz-Kriterium.
Inhaltsverzeichnis
Konvergenzgeschwindigkeit
Das Restglied der Summe für Pi nach n Summanden beträgt
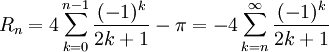 .
.
Mit der Fehlerabschätzung des Leibniz-Kriteriums gilt
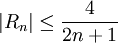 .
.
Genauere Betrachtungen zeigen sogar, dass
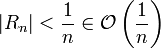 .
.
Mit
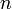 Summanden kann man also
Summanden kann man also  Nachkommastellen mit einem Fehler < 0,5 in der
Nachkommastellen mit einem Fehler < 0,5 in der  -ten Nachkommastelle erhalten:
-ten Nachkommastelle erhalten:Die Anzahl benötigter Summanden
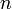 für
für  sinnvolle Nachkommastellen im Ergebnis beträgt entsprechend
sinnvolle Nachkommastellen im Ergebnis beträgt entsprechendVerbesserte Konvergenzgeschwindigkeit durch ein zusätzliches Korrekturglied
Die Partialsumme oszilliert, da sie das Leibniz-Kriterium erfüllt, stets um den Wert der unendlichen Reihe herum. Der Grenzwert liegt dabei in etwa in der Mitte zwischen zwei aufeinanderfolgenden Partialsummen. Das kann man nutzen um eine verbesserte Version der Formel zu erzeugen, indem man vom nächsten Glied nach der Reihe noch die Hälfte addiert.
Eine verbesserte Formel ist somit:
Das Restglied ist dann beschränkt durch
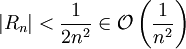 .
.
Damit ist der Zusammenhang zwischen der Anzahl Summenglieder
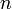 und sinnvollen Nachkommastellen
und sinnvollen Nachkommastellen 
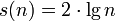
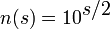
Eine Liste von Partialsummen, die sich aus Leibniz' Formel ergeben
Mit Hilfe der Leibniz-Reihe lässt sie eine Näherung der Kreiszahl berechnen, denn es ist
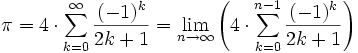 .
.
Die folgende Liste zeigt die Folgenglieder der Folge von Partialsummen der mit 4 multiplizierten Leibniz-Reihe.
Da die Folge nur sehr langsam konvergiert, ist sie zur effizienten Berechnung von Pi nicht geeignet.
n
(Anzahl der
berechneten
Brüche)
(Ergebnis)Verhältnis
zur
Kreiszahl2 2,666666666666667 0,848826363156775 4 2,895238095238095 0,921582908570213 8 3,017071817071817 0,960363786700453 16 3,079153394197426 0,980124966449415 32 3,110350273698686 0,990055241612751 64 3,125968606973288 0,995026711499770 100 3,131592903558553 0,996816980705689 1.000 3,140592653839793 0,999681690193394 10.000 3,141492653590043 0.999968169011461 100.000 3,141582653589793 0,999996816901138 1.000.000 3,141591653589793 0,999999681690114 10.000.000 3,141592553589793 0,999999968169011 100.000.000 3,141592643589793 0,999999996816901 1.000.000.000 3,141592652589793 0,999999999681690 Diese Liste wurde mit einem Java-Programm erstellt und mit bc korrigiert.
Siehe auch:
Wikimedia Foundation.