- Kugelsymmetrie
-
Mit dem geometrischen Begriff Symmetrie (von griechisch syn (=zusammen) und metron (=Maß)) bezeichnet man die Eigenschaft, dass ein geometrisches Objekt durch bestimmte Umwandlungen auf sich selbst abgebildet werden kann, also unverändert erscheint. Eine Umwandlung, die ein Objekt auf sich selbst abbildet, heißt Symmetrieoperation. Zwei verschiedene geometrische Objekte können zueinander symmetrisch sein, nämlich dann, wenn eine Symmetrieoperation existiert, die das eine Objekt in das andere überführt.
Abhängig von der Zahl der betrachteten Dimensionen gibt es folgende unterschiedliche Symmetrien:
Symmetrien im Eindimensionalen
Im Eindimensionalen, also auf einer Geraden, gibt es die Symmetrie bezüglich eines einzelnen Punktes sowie die Symmetrie bezüglich Translation (Verschiebung).
Symmetrien im Zweidimensionalen
Im Zweidimensionalen muss zwischen Punkt- und Achsensymmetrie unterschieden werden.
Achsensymmetrie
Die Achsensymmetrie, axiale Symmetrie oder Spiegelsymmetrie[1] ist eine Form der Symmetrie, die bei Dingen auftritt, die entlang einer Symmetrieachse gespiegelt sind.
Verschiedenes:
- Dreiecke können eine oder drei Symmetrieachsen haben: Ein gleichschenkliges Dreieck ist achsensymmetrisch bezüglich der Mittelsenkrechten zur Basis. Gleichseitige Dreiecke haben drei Symmetrieachsen.
- Vierecke können eine, zwei oder sogar vier Symmetrieachsen besitzen:
- Mindestens eine Symmetrieachse haben gleichschenklige Trapeze (durch die Mittelpunkte der parallelen Seiten) und Drachenvierecke (entlang einer Diagonale).
- Mindestens zwei Symmetrieachsen liegen vor beim Rechteck (die Mittelsenkrechten von gegenüber liegenden Seiten) und bei der Raute (beide Diagonalen).
- Das Quadrat schließlich ist Rechteck und Raute zugleich und weist somit vier Symmetrieachsen auf.
- Kreise weisen sogar unendlich viele Symmetrieachsen auf, da sie bezüglich jedes Durchmessers symmetrisch sind.
- Eine weitere Figur mit unendlich vielen Symmetrieachsen ist die Gerade. Da sie unendlich lang ist, ist sie symmetrisch bezüglich jeder zu ihr senkrechten Achse sowie der auf ihr selbst liegenden Achse.
Achsensymmetrie von Funktionsgraphen
Eine vor allem in der Schulmathematik beliebte Aufgabenstellung besteht darin, für den Graphen einer Funktion die Achsensymmetrie nachzuweisen. Dieser Nachweis ist besonders einfach im Falle der Symmetrie bezüglich der y-Achse des (kartesischen) Koordinatensystems. Eine Funktion ist achsensymmetrisch bezüglich der y-Achse, wenn gilt:
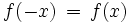
Ist sie für alle x gültig, liegt Achsensymmetrie vor, das heißt f ist eine gerade Funktion.
Diese Bedingung läuft darauf hinaus, dass die Funktionswerte für die entgegengesetzt gleichen Argumente x und − x übereinstimmen müssen.
Als Beispiel soll die Gleichung einer einfachen quadratischen Funktion dienen:
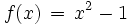
Anwendung der genannten Bedingung ergibt:
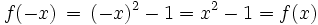
Der Graph (eine Parabel) ist also tatsächlich symmetrisch bezüglich der y-Achse.
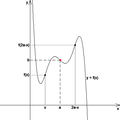
Allgemeiner gilt: Der Graph einer Funktion f ist genau dann achsensymmetrisch bezüglich der Geraden mit der Gleichung x = a, wenn die folgende Bedingung für beliebige Werte von x richtig ist:
Durch Substitution von x mit x − a erhält man die äquivalente Bedingung:
Beispiel einer Funktion mit achsensymmetrischem Graphen
Graph der Funktion f mit der Gleichung y = f(x) = x2 − 4x + 3; Achsensymmetrie bezüglich der Geraden mit der Gleichung x = 2 (es gilt also a = 2)
Damit ist die Vermutung der Achsensymmetrie bestätigt.
Punktsymmetrie
Die Punktsymmetrie, auch Zentralsymmetrie[1], ist eine Eigenschaft geometrischer Objekte. Ein geometrisches Objekt (z. B. ein Viereck) heißt (in sich) punktsymmetrisch, wenn es eine Punktspiegelung gibt, die dieses Objekt auf sich abbildet. Der Punkt, an dem diese Spiegelung erfolgt, wird als Symmetriezentrum bezeichnet. Obwohl eine solche Punktspiegelung einer Drehung um 180° entspricht, ist die Punktsymmetrie von der Drehsymmetrie zu unterscheiden. Sie bildet lediglich den Spezialfall einer Drehsymmetrie. Die folgende Abbildung zeigt einige punktsymmetrische Figuren.
Zwei verschiedene Objekte können zueinander punktsymmetrisch sein, nämlich dann, wenn eine Punktspiegelung existiert, die das eine Objekt in das andere überführt.
Verschiedenes:
- Ein Dreieck kann nicht in sich punktsymmetrisch sein, wohl aber zwei Dreiecke zueinander.
- Bei einem Viereck liegt Punktsymmetrie (in sich) genau dann vor, wenn es sich um ein Parallelogramm handelt. Das Symmetriezentrum ist in diesem Fall der Schnittpunkt seiner Diagonalen. Als Sonderfälle des Parallelogramms sind auch Rechteck, Raute und Quadrat punktsymmetrisch.
- Jeder Kreis ist (in sich) punktsymmetrisch bezüglich seines Mittelpunkts.
- Zwei Kreise mit gleichem Radius sind zueinander punktsymmetrisch. Das Symmetriezentrum ist der Mittelpunkt der Verbindungsstrecke zwischen den beiden Kreismittelpunkten.
- Mehrere Symmetriezentren kann es nur geben, wenn die Figur nicht beschränkt ist. Das einfachste Beispiel ist die Gerade. Sie hat sogar unendlich viele Symmetriezentren.
Punktsymmetrie von Funktionsgraphen
Eine vor allem in der Schulmathematik häufige Aufgabenstellung besteht darin nachzuweisen, dass der Graph einer gegebenen Funktion punktsymmetrisch ist. Dieser Nachweis kann mit der folgenden Formel geführt werden:
Ist diese Gleichung für alle x erfüllt, liegt Punktsymmetrie zum Punkt P = (a | b) vor. Die genannte Bedingung ist durch Substitution von x mit x − a gleichwertig zu
Im Spezialfall P = (0 | 0) vereinfacht sich diese Gleichung:
Ist sie für alle x gültig, liegt Punktsymmetrie zum Koordinatenursprung vor, das heißt f ist eine ungerade Funktion.
Beispiel mit Punktsymmetrie zum Koordinatenursprung
Geg.: f(x) = 2x5
− f( − x) = − (2( − x)5)
= − 2( − 1)5x5
= − 2( − 1)x5
= 2x5 = f(x)→ Der Funktionsgraph ist punktsymmetrisch zum Ursprung (0 | 0).
Beispiel mit Punktsymmetrie zum Punkt P = (0|2)
Geg.: f(x) = 2x5 + 2
P = (a | b) = (0 | 2) → a = 0, b = 2
2b − f(2a − x) = 4 − f( − x) = 4 − (2( − x)5 + 2)
= 4 − ( − 2x5 + 2)
= 4 + 2x5 − 2
= 2x5 + 2 = f(x)→ Der Funktionsgraph ist punktsymmetrisch zu P = (0 | 2)!
Also ist − f(x) + 2 = f( − x) − 2.
Symmetrien im Dreidimensionalen
Der Achsensymmetrie im Zweidimensionalen entspricht die Flächensymmetrie im Dreidimensionalen, der Punktsymmetrie die Achsensymmetrie (Drehsymmetrie um 180°). Daneben gibt es noch die Punktsymmetrie (= Zentralsymmetrie) im Raum, die eine seltenere Rolle in der Praxis spielt.
Natur
Der Aufbau der meisten höheren Lebewesen ist mehr oder weniger annähernd spiegelsymmetrisch (bei niederen Lebensformen findet sich oft Achsensymmetrie, diese bilden somit einen angenäherten Rotationskörper). Auch der Mensch verfügt über eine vertikale Symmetrieebene. Diese Symmetrie ist dabei jedoch nicht vollständig, so ist der Aufbau der inneren Organe nicht spiegelsymmetrisch. Auch die scheinbar zueinander symmetrischen Körperteile wie Augen, Ohren, Arme, Beine, Brüste etc. weisen untereinander immer mehr oder weniger große Lage-, Form- und Größenunterschiede auf.
Symmetrien in mehr als drei Dimensionen
In Räumen mit n Dimensionen gibt es entsprechend den obigen Beispielen n verschiedene Symmetrien.
Translationssymmetrie
Symmetrie gegenüber einer (Parallel-)Verschiebung (Translationssymmetrie)
Rotationssymmetrie
Dreidimensionale Objekte sind rotationssymmetrisch, wenn eine Drehung um jeden beliebigen Winkel um eine Achse (die Symmetrieachse) das Objekt auf sich selbst abbildet.
Rotationssymmetrie um eine Achse wird auch als Zylindersymmetrie bezeichnet. Dreidimensionale geometrische Objekte mit dieser Eigenschaft nennt man auch Rotationskörper.
Bei zweidimensionalen Objekten gilt dies dementsprechend bei Drehung um einen Punkt. Diese Symmetrie wird auch als Kreissymmetrie bezeichnet.
Kugelsymmetrie
Rotationssymmetrie um jede beliebige Achse durch denselben Punkt ist ein Spezialfall der Rotationssymmetrie und wird als Kugelsymmetrie bezeichnet.
Sterne sind z. B. annähernd kugelsymmetrisch, da deren Eigenschaften (wie z. B. die Dichte) zwar nicht überall gleich sind, aber nur vom Abstand zum Mittelpunkt abhängen.
Auch deren Schwerefelder sowie z. B. das elektrische Feld einer geladenen Kugel sind kugelsymmetrisch.
Kombinationen
Aus der Möglichkeit, Symmetrieoperationen zu kombinieren, lassen sich die symmetrischen Grundoperationen herleiten:
- Identität (Null-Operation, keine Veränderung)
- Rotation (Drehung)
- Rotation – Inversion (Drehspiegelung)
- Translation (Verschiebung)
- Gleitspiegelung
Siehe auch
Einzelnachweise
Literatur
- H. Schupp: Elementargeometrie. UTB Schöningh 1977, ISBN 3-506-99189-2, S. 35, 45
Weblinks
Wikimedia Foundation.



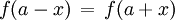
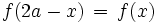
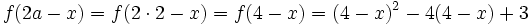
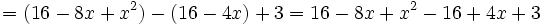
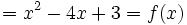
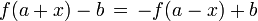
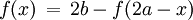
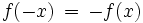
_=_2xE5.png)
_=_2xE5_plus_2.png)