Künstliche neuronale Netzwerke

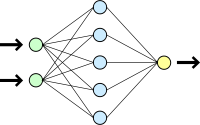
Künstliche neuronale Netze (kurz: KNN, engl. artificial neural network – ANN) sind Netze aus künstlichen Neuronen. Sie sind ein Zweig der künstlichen Intelligenz und prinzipieller Forschungsgegenstand der Neuroinformatik. Der Ursprung der künstlichen neuronalen Netze liegt, ebenso wie bei den künstlichen Neuronen, in der Biologie. Man stellt sie den natürlichen neuronalen Netzen gegenüber, welche Nervenzellvernetzungen im Gehirn und im Rückenmark bilden. Insgesamt geht es aber um eine Abstraktion (Modellbildung) von Informationsverarbeitung und weniger um das Nachbilden biologischer neuronaler Netze.

Vereinfachte Darstellung eines künstlichen neuronalen Netzes

Schema eines künstlichen Neurons

Beschreibung

Künstliche neuronale Netze basieren meist auf der Vernetzung vieler McCulloch-Pitts-Neuronen oder leichter Abwandlungen davon. Grundsätzlich können auch andere künstliche Neuronen Anwendung in KNNen finden, z.B. das High-Order-Neuron. Die Topologie eines Netzes (die Zuordnung von Verbindungen zu Knoten) muss abhängig von seiner Aufgabe gut durchdacht sein. Nach der Konstruktion eines Netzes folgt die Trainingsphase, in der das Netz „lernt“. Theoretisch kann ein Netz durch folgende Methoden lernen:

• Entwicklung neuer Verbindungen, Löschen bestehender Verbindungen
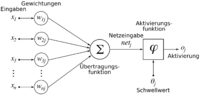
• Ändern der Wichtung (der Gewichte w_ij von Neuron i zu Neuron j)
• Anpassen der Schwellwerte der Neuronen
• Hinzufügen oder Löschen von Neuronen

Außerdem verändert sich das Lernverhalten bei Veränderung der Aktivierungsfunktion der Neuronen oder der Lernrate des Netzes. Praktisch gesehen "lernt" ein Netz hauptsächlich durch Modifikation der Gewichte der Neuronen. Eine Anpassung des Schwellwertes kann hierbei durch ein Bias-Neuron (englisch to bias heißt hier etwa verzerren) mit erledigt werden. Dadurch sind KNNs in der Lage, komplizierte nichtlineare Funktionen über einen „Lern”-Algorithmus, der durch iterative oder rekursive Vorgehensweise aus vorhandenen Eingangs- und gewünschten Ausgangswerten alle Parameter der Funktion zu bestimmen versucht, zu erlernen. KNNs sind dabei eine Realisierung des konnektionistischen Paradigmas, da die Funktion aus vielen einfachen gleichartigen Teilen besteht. Erst in ihrer Summe wird das Verhalten komplex. Neuronale Netze stellen von der Berechenbarkeit her ein äquivalentes Modell zur Turingmaschine dar ^[1].

Geschichtliche Entwicklung

Der Anfang der neuronalen Netze war bereits in den frühen 1940er, also fast zeitgleich mit der Geschichte der programmierbaren Computer.^[2]

Anfänge

Die Anfänge gehen auf Warren McCulloch und Walter Pitts zurück. Diese beschreiben 1943 eine Art neurologisches Netzwerk, das praktisch jede logische oder auch arithmetische Funktion berechnen kann. 1947 weisen sie daraufhin, dass ein solches Netzwerk zu räumlichen Mustererkennung eingesetzt werden kann. 1949 formuliert Donald O. Hebb seine Hebbsche Lernregel, die in ihrer allgemeinen Form fast alle neuronalen Lernverfahren darstellt. Karl Lashley kommt 1950 zu der These, dass der Prozess der Informationsspeicherung verteilt im Gehirn realisiert wird.

Blütezeit

Im anschließenden Jahr, 1951, gelingt Marvin Minsky mit seiner Dissertationsarbeit der Bau des Neurocomputers Snark, der seine Gewichte automatisch justieren kann, jedoch nicht praktisch einsetzbar ist. 1956 treffen sich Wissenschaftler und Studenten auf dem Dartmouth Summer Research Project. Von 1957-1958 entwickeln Frank Rosenblatt und Charles Wightman den ersten erfolgreichen Neurocomputer, mit dem Namen Mark I Perceptron. Der Computer konnte mit seinem 20 x 20 Pixel großen Bildsensor bereits einfache Ziffern erkennen. Im nachfolgenden Jahr formuliert Rosenblatt das Perceptron-Konvergenz-Theorem. 1960 stellen Bernhard Widrow und Marcian E. Hoff das ADALINE (ADAptive Linear Neuron) vor.^[3] Dieses Netzwerk erreichte als erstes weite kommerzielle Verbreitung. Anwendung fand es in Analogtelefonen zur Echtzeit-Echofilterung. Das Neuronale Netz lernte mit der Deltaregel. 1961 stellte Karl Steinbuch Techniken der assoziativen Speicherung vor. 1969 gaben Marvin Minsky und Seymour Papert eine genaue mathematische Analyse des Perceptrons.^[4] Sie zeigten auf, dass wichtige Probleme nicht gelöst werden können. So sind unter anderem XOR-Operatoren nicht auflösbar und es gibt Probleme in der linearen Separierbarkeit. Die Folge war ein vorläufiges Ende der Forschungen auf dem Gebiet der Neuronalen Netze, da die meisten Forschungsgelder gestrichen wurden.

Langsamer Wiederaufbau

1972 stellt Teuvo Kohonen den linearen Assoziators, ein Modell des Assoziativspeichers, vor.^[5] James A. Anderson beschreibt das Modell unabhängig von Kohonen aus neuropsychologischen Sicht im selben Jahr.^[6] 1973 benutzt Christoph von der Malsburg ein Neuronenmodell, das nichtlinear ist. Bereits 1974 entwickelt Paul Werbos für seine Dissertation die Backpropagation bzw. die Fehlerrückführung. Das Modell bekam aber erst später eine größere Bedeutung. Ab 1976 entwickelt Stephen Grossberg mathematisch fundierte Modelle neuronaler Netze. Zusammen mit Gail Carpenter widmet er sich auch dem Problem ein Neuronales Netzwerk lernfähig zu halten ohne bereits gelerntes zu zerstören. Sie formulieren ein Architekturkonzept für Neuronale Netze, die Adaptive Resonanztheorie. 1982 beschreibenTeuvo Kohonen die nach ihm benannten selbstorganisierenden Karten. Im selben Jahr beschreibt John Hopfield das Modell der Hopfieldnetze. 1983 wird von Kunihiko Fukushima, S. Miyake und T. Ito das neuronale Modell Neocognitron vorgestellt. Das Modell ist eine Weiterentwicklung des 1975 entwickelten Cognitrons und dient zur Erkennung handgeschriebener Zeichen.

Renaissance

1985 veröffentlicht John Hopfield eine Lösung des Travelling Salesman Problems durch das Hopfieldnetz. 1985 wird das Lernverfahren Backpropagation of Error als Verallgemeinerung der Delta-Regel durch die Parallel Distributed Processing-Gruppe separat entwickelt. Somit werden nicht linear separierbare Problems durch mehrschichtige Perceptrons lösbar. Minskys Abschätzung war also widerlegt.

Anwendung

Seine besonderen Eigenschaften machen das KNN bei allen Anwendungen interessant, bei denen kein bzw. nur geringes explizites (systematisches) Wissen über das zu lösende Problem vorliegt. Dies sind z.B. die Texterkennung, Bilderkennung und Gesichtserkennung, bei denen einige Hunderttausend bis Millionen Bildpunkte in eine im Vergleich dazu geringe Anzahl von erlaubten Ergebnissen überführt werden müssen.

Auch in der Regelungstechnik kommen KNN zum Einsatz, um herkömmliche Regler zu ersetzen oder ihnen Sollwerte vorzugeben, die das Netz aus einer selbst entwickelten Prognose über den Prozessverlauf ermittelt hat.

Die Anwendungsmöglichkeiten sind aber nicht auf techniknahe Gebiete begrenzt: Bei der Vorhersage von Veränderungen in komplexen Systemen werden KNNs unterstützend hinzugezogen, z.B. zur Früherkennung sich abzeichnender Tornados oder aber auch zur Abschätzung der weiteren Entwicklung wirtschaftlicher Prozesse.

Zu den Anwendungsgebieten von KNNs gehören:

• Regelung und Analyse von komplexen Prozessen
• Frühwarnsystemen
• Optimierung
• Zeitreihenanalyse (Wetter, Aktien etc.)
• Sprachgenerierung (Beispiel: NETtalk)
• Bildverarbeitung und Mustererkennung
  • Schrifterkennung (OCR)
  • Spracherkennung
  • Data-Mining
• Informatik: Bei Robotik, virtuellen Agenten und KI-Modulen in Spielen und Simulationen.
• Klangsynthese

Biologische Motivation

Während das Gehirn zur massiven Parallelverarbeitung in der Lage ist, arbeiten die meisten heutigen Computersysteme nur sequentiell (bzw. partiell parallel eines Rechners). Es gibt jedoch auch erste Prototypen neuronaler Rechnerarchitekturen, sozusagen den neuronalen Chip, für die das Forschungsgebiet der künstlichen neuronalen Netze die theoretischen Grundlagen bereitstellt. Dabei werden die physiologischen Vorgänge im Gehirn jedoch nicht nachgebildet, sondern nur die Architektur der massiv parallelen Analog-Addierer in Silizium nachgebaut, was gegenüber einer Software-Emulation eine bessere Performance verspricht.

Klassen und Typen von KNN

Grundsätzlich unterscheiden sich die Klassen der Netze vorwiegend durch die unterschiedlichen Netztopologien und Verbindungsarten. Beispielsweise einschichtige-, mehrschichtige-, Feedforward- oder Feedback-Netze.

• McCulloch-Pitts-Netze
• Lernmatrix
• Hopfield-Netze
• Perzeptron
  • Adaline-Modell
• Self-Organizing Maps (auch Kohonen-Netze) (SOM)
• Growing Neural Gas (GNG)
• Lernende Vektorquantisierung (LVQ)
• Bidirektionaler Assoziativspeicher (BAM)
• Boltzmann-Maschine
• Cascade Correlation Netze
• Counterpropagation Netze
• Probabilistische Neuronale Netze
• Radiale Basisfunktions-Netze (RBF)
• Adaptive Resonanztheorie (ART)
• Neocognitron
• Pulscodierte Neuronale Netze (PCNN)
• Time Delay Neural Networks (TDNNs)
• Rekurrente Neuronale Netze (RNNs)
  • Elman-Netze (auch Simple recurrent network, SRN)
  • Jordan-Netze
• Oszillierendes Neuronales Netzwerk

Lernverfahren

Lernverfahren dienen dazu, ein neuronales Netz dazu zu bringen, für bestimmte Eingangsmuster zugehörige Ausgabemuster zu erzeugen. Dies geschieht grundsätzlich auf drei verschiedenen Wegen.

Überwachtes Lernen

Beim Überwachten Lernen wird dem neuronalen Netz ein Eingangsmuster gegeben und die Ausgabe, die das Neuronale Netz in seinem aktuellen Zustand produziert, mit dem Wert verglichen, den es eigentlich ausgeben soll. Durch Vergleich von Soll- und Istausgabe kann auf die vorzunehmenden Änderungen der Netzkonfiguration geschlossen werden.

• Delta-Regel (auch Perzeptron-Lernregel)
• Backpropagation
  • Backpropagation mit Trägheitsterm
  • SuperSAB
  • Quickprop
  • Resilient Propagation

Bestärkendes Lernen

Es ist nicht immer möglich, zu jedem Eingabedatensatz den passenden Ausgabedatensatz zum Trainieren zur Verfügung zu haben. Zum Beispiel kann man einem Agenten, der sich in einer fremden Umgebung zurechtfinden muss - etwa einem Roboter auf dem Mars - nicht zu jedem Zeitpunkt sagen, welche Aktion jeweils die beste ist. Aber man kann dem Agenten eine Aufgabe stellen, die dieser selbstständig lösen soll. Nach einem Testlauf, der aus mehreren Zeitschritten besteht, kann der Agent bewertet werden. Aufgrund dieser Bewertung kann eine Agentenfunktion gelernt werden.

Der Lernschritt kann durch eine Vielzahl von Techniken vollzogen werden. Unter anderem können hier auch künstliche neuronale Netze zum Einsatz kommen.

Unüberwachtes Lernen

Das Unüberwachte Lernen erfolgt ausschließlich durch Eingabe der zu lernenden Muster. Das Neuronale Netz verändert sich entsprechend den Eingabemustern von selbst.

• Hebbsche Lernregel
• Kohonennetze

Stochastisches Lernen

• Simulated Annealing

Allgemeine Probleme

Die Hauptnachteile von KNN sind gegenwärtig

1. Das Trainieren von KNN (im Terminus der Statistik: Das Schätzen der im Modell enthaltenen Parameter) führt in der Regel zu hochdimensionalen, nichtlinearen Optimierungsproblemen. Die prinzipielle Schwierigkeit bei der Lösung dieser Probleme besteht in der Praxis häufig darin, dass man nicht sicher sein kann, ob man das globale Optimum gefunden hat oder nur ein lokales. Obgleich in der Mathematik eine Fülle relativ schnell konvergierender lokaler Optimierungsverfahren entwickelt wurden (beispielsweise Quasi-Newton-Verfahren: BFGS, DFP usw.), finden auch diese selten optimale Lösungen. Eine zeitaufwändige Näherung an die globale Lösung erreicht man ggf. durch die vielfache Wiederholung der Optimierung mit immer neuen Startwerten.
2. Es müssen Trainingsdaten gesammelt oder manuell erzeugt werden. Dieser Vorgang kann sehr schwierig sein, da man verhindern muss, dass das Netz Eigenschaften der Muster lernt, die zwar auf dem Trainingsset mit dem Ergebnis in irgendeiner Weise korreliert sind, die aber in anderen Situationen nicht zur Entscheidung herangezogen werden können. Wenn bspw. die Helligkeit von Trainingsbildern bestimmte Muster aufweist, dann 'achtet' das Netz unter Umständen nicht mehr auf die gewünschten Eigenschaften, sondern klassifiziert die Daten nur noch aufgrund der Helligkeit.
3. Bei Anwendung einer ‚heuristischen‘ – nicht statistischen – Vorgehensweise bei der Netzwerkspezifikation, neigen KNN dazu, die Trainingsdaten einfach auswendig zu lernen (Überanpassung). Wenn dies geschieht, können sie nicht mehr auf neue Daten verallgemeinern. Um Überanpassung zu vermeiden, muss die Netzwerkarchitektur sehr ‚vorsichtig‘ gewählt werden. Dieses Problem existiert auch bei vielen anderen statistischen Verfahren und wird als ‚bias-variance trade-off‘ bezeichnet. Seit einigen Jahren werden häufig verbesserte Verfahren (Boosting, Support-Vector-Maschinen, Regularisierungsnetzwerke) eingesetzt, die diesem Problem begegnen.
4. Die Kodierung der Trainingsdaten muss problemangepasst und nach Möglichkeit redundanzfrei gewählt werden. In welcher Form die zu lernenden Daten dem Netz präsentiert werden, hat einen großen Einfluss auf die Lerngeschwindigkeit, sowie darauf, ob das Problem überhaupt von einem Netz gelernt werden kann. Gute Beispiele hierfür sind Sprachdaten, Musikdaten oder auch Texte. Das einfache Einspeisen von Zahlen, beispielsweise einer Wavdatei für Sprache, führt selten zu einem erfolgreichen Ergebnis. Je präziser das Problem allein durch die Vorverarbeitung und Kodierung gestellt wird, desto erfolgreicher kann ein KNN dieses verarbeiten.

Siehe auch

• Aktivierungsraum
• Konnektionismus
• künstliche Intelligenz
• künstliches Neuron
• Maschinenlernen
• Mustererkennung
• Neuroinformatik
• Neuronaler Schaltkreis
• Neuronales Netz
• Parallel Distributed Processing
• Perzeptron
• Topologie (Künstliche neuronale Netze)

Einzelnachweis

1. ↑ http://www.math.rutgers.edu/~sontag/FTP_DIR/aml-turing.ps.gz
2. ↑ http://www.dkriesel.com/index.php?id=neuronalenetze, Stand: 28.02.2009
3. ↑ Widrow, Bernhard/Hofff, Marcian: „Adaptive switching circuits“. In ‘‘Proceedings WESCON, p. 96-104, 1960.
4. ↑ Minsky, Marvin/Papert, Seymour: „Perceptrons“, MIT Press, Cambridge 1969.
5. ↑ Kohonen, Teuvo: "Correlation matrix memories. IEEEtC", 1972.
6. ↑ Anderson, James: "A simple neural network generating an interactive memory. Mathematical Biosciences", 1972.

Literatur

• A. Lucas: Schätzung und Spezifikation ökonometrischer neuronaler Netze. ISBN 3-89936-183-0
• Andreas Zell: Simulation neuronaler Netze. ISBN 3-486-24350-0.
• B. Lenze: Einführung in die Mathematik neuronaler Netze. ISBN 3-89722-021-0
• Günter Daniel Rey, Karl F. Wender: Neuronale Netze. Eine Einführung in die Grundlagen, Anwendungen und Datenauswertung. ISBN 3-456-84513-8.
• H. Rehkugler, H.G. Zimmermann: Neuronale Netze in der Ökonomie. ISBN 3-800-61871-0
• Helge Ritter, Thomas Martinetz, Klaus Schulten: Neural Computation and Self-Organizing Maps: An Introduction. Addison Wesley - Verlag (Februar 1992) ISBN 0201554429
• Johann Gasteiger, J. Zupan: Neural Networks in Chemistry and Drug Design ISBN 3-527-29779-0
• John A. Hertz, Richard G. Palmer, Anders Krogh: Introduction to the Theory of Neural Computation - Westview Press; New Edition (January 1, 1991) ISBN 0201515601
• Raúl Rojas: Theorie der Neuronalen Netze. ISBN 3-540-56353-9.
• Simeon Knieling: Einführung in die Modellierung künstlich neuronaler Netzwerke. WiKu-Verlag, Duisburg 2007, ISBN 978-3-86553-192-6.
• Simon Haykin: Neural Networks: A Comprehensive Foundation. ISBN 0-13-273350-1.
• Teuvo Kohonen: Self Organizing Maps. ISBN 3-540-67921-9

Weblinks

• Einführung in die Grundlagen und Anwendungen neuronaler Netze
• Ein kleiner Überblick über Neuronale Netze - Grundlagenskript zu zahlreichen Arten / Lernprinzipien Neuronaler Netze, viele Abbildungen, einfach geschrieben, ca. 200 Seiten (PDF).
• Einführung in Neuronale Netze
• Geschichte der Neuronalen Netze bis 1960 (engl.)
• Tutorial zum Thema KNN
• Brain Cells Fused with Computer Chip
• Links zum Thema Neuronale Netze im Open Directory Project
• Gute Einführung in neuronale Netzwerke (engl.)

Implementierungen und Simulationspakete

• ANNSI - Simulator für Künstliche Neuronale Netze
• Emergent, Rewrite des bekannten PDP++
• SNNS - Stuttgarter Neuronale-Netze-Simulator
• FANN-Bibliothek – fast artificial neural network: http://fann.sourceforge.net/
• Lightweight neural network: http://lwneuralnet.sourceforge.net/
• KNN-Implementierungen auf linux-related.de
• EpsiloNN neuronale Beschreibungssprache der Universität Ulm
• Java Object Oriented Neural Engine
• MemBrain - Graphischer Neuronale-Netze-Editor und -Simulator für Windows
• auto-nng - Automatischer Neuronale-Netze-Generator für BSD / Linux