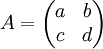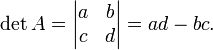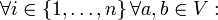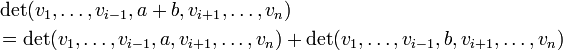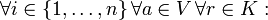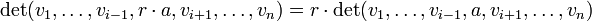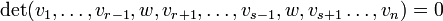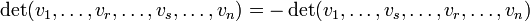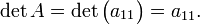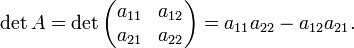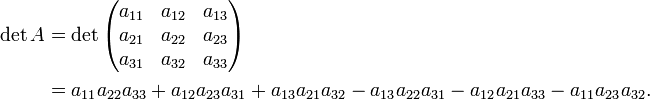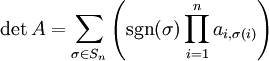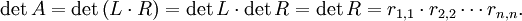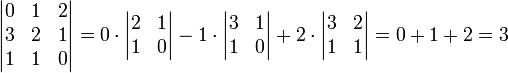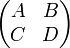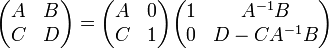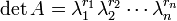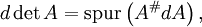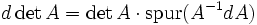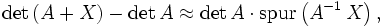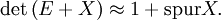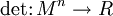- Laplace-Entwicklung
-
In der Linearen Algebra ist die Determinante eine spezielle Funktion, die einer quadratischen Matrix oder einem linearen Endomorphismus eine Zahl zuordnet. Zum Beispiel hat die
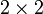 -Matrix
-Matrixdie Determinante
Die Formel für größere Matrizen wird weiter unten angegeben.
Die Determinante einer Matrix A wird auch als | A | geschrieben. Diese Notation kann jedoch zu Verwechslungen führen, da sie auch für andere Matrix-Funktionen wie beispielsweise die Quadratwurzel aus A * A verwendet wird.
Mit Hilfe von Determinanten kann man feststellen, ob ein Lineares Gleichungssystem eindeutig lösbar ist. Dies ist genau dann der Fall, wenn die Determinante der Koeffizientenmatrix ungleich null ist. Entsprechend ist eine quadratische Matrix genau dann invertierbar wenn ihre Determinante ungleich null ist.
Man bildet die Determinante von n Vektoren im
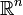 , indem man die Determinante der quadratischen Matrix berechnet, deren Spalten die gegebenen Vektoren sind. Mit dieser Festlegung kann das Vorzeichen der Determinante einer Basis dazu verwendet werden, den Begriff der Orientierung in Euklidischen Räumen zu definieren.
, indem man die Determinante der quadratischen Matrix berechnet, deren Spalten die gegebenen Vektoren sind. Mit dieser Festlegung kann das Vorzeichen der Determinante einer Basis dazu verwendet werden, den Begriff der Orientierung in Euklidischen Räumen zu definieren.Determinanten werden zur Berechnung von Volumina in der Vektorrechnung verwendet: der Absolutbetrag der Determinante von reellen Vektoren ist gleich dem Volumen des Parallelepipeds (auch Spat genannt), das durch diese Vektoren aufgespannt wird. Eine Folgerung ist: Wird die lineare Abbildung
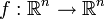 durch die Matrix A repräsentiert, und ist
durch die Matrix A repräsentiert, und ist 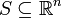 eine beliebige messbare Teilmenge, dann ist das Volumen von f(S) durch
eine beliebige messbare Teilmenge, dann ist das Volumen von f(S) durch 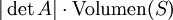 gegeben. Allgemeiner gilt: Wird die lineare Abbildung
gegeben. Allgemeiner gilt: Wird die lineare Abbildung 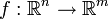 durch die
durch die 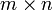 -Matrix A repräsentiert, und ist
-Matrix A repräsentiert, und ist 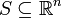 eine beliebige messbare Teilmenge, so ist das n-dimensionale Volumen von f(S) gegeben durch
eine beliebige messbare Teilmenge, so ist das n-dimensionale Volumen von f(S) gegeben durch 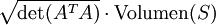 .
.Inhaltsverzeichnis
Geschichte
Historisch gesehen wurden Determinanten bereits vor den Matrizen betrachtet. Ursprünglich war eine Determinante als eine Eigenschaft eines linearen Gleichungssystems definiert. Die Determinante „determiniert“, ob das Gleichungssystem eine eindeutige Lösung besitzt (dies ist genau dann der Fall, wenn die Determinante ungleich Null ist). In diesem Zusammenhang wurden 2×2-Matrizen von Cardano Ende des 16. Jahrhunderts und größere von Leibniz ungefähr 100 Jahre später behandelt.
Definition und Berechnung
Definition über die Eigenschaften
Allgemein heißt eine Abbildung vom Raum der quadratischen Matrizen einer bestimmten Größe in den zugrundeliegenden Körper eine Determinante, wenn sie folgende drei Eigenschaften erfüllt:
- sie ist multilinear, d. h. linear in jeder Spalte:
- sie ist alternierend, d. h. wenn in zwei Spalten das gleiche Argument steht, ist die Determinante gleich 0:
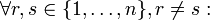
- Hieraus folgt, dass sich gerade das Vorzeichen ändert, wenn man zwei Spalten vertauscht:
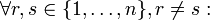
- Oft wird diese Folgerung zur Definition von alternierend verwendet. Im Allgemeinen ist diese jedoch nicht zur obigen äquivalent!
- Wenn man alternierend nämlich auf die zweite Weise definiert, gibt es keine eindeutige Determinantenform, wenn der Körper über den wir unseren Vektorraum bilden der Körper mit nur zwei Elementen ist.
- sie ist normiert, d. h. die Einheitsmatrix hat die Determinante 1
- detEn = 1
Man kann beweisen, dass es genau eine solche Abbildung gibt.
Für Endomorphismen endlichdimensionaler Vektorräume schreibt man
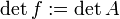 , falls f bezüglich einer Basis durch die Matrix A dargestellt wird. (Dies ist unabhängig von der Wahl der Basis.)
, falls f bezüglich einer Basis durch die Matrix A dargestellt wird. (Dies ist unabhängig von der Wahl der Basis.)Matrizen bis zur Größe 3×3
Für eine nur aus einem Koeffizienten bestehende
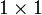 -Matrix A ist
-Matrix A istIst A eine
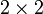 -Matrix, dann ist
-Matrix, dann istFür eine
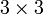 -Matrix A gilt die Formel
-Matrix A gilt die FormelWill man diese Determinante von Hand berechnen, so stellt die Regel von Sarrus dafür ein einfaches Schema zur Verfügung.
Leibniz-Formel
Für eine allgemeine
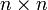 -Matrix wurde die Determinante von Gottfried Leibniz durch die heute als Leibniz-Formel bekannte Formel definiert:
-Matrix wurde die Determinante von Gottfried Leibniz durch die heute als Leibniz-Formel bekannte Formel definiert:Die Summe wird über alle Permutationen σ der Zahlen
 berechnet und
berechnet und  bezeichnet das Vorzeichen der Permutation σ: +1, falls σ eine gerade Permutation ist und -1, falls sie ungerade ist.
bezeichnet das Vorzeichen der Permutation σ: +1, falls σ eine gerade Permutation ist und -1, falls sie ungerade ist.Ob eine Permutation gerade oder ungerade ist, erkennt man daran, wie viele Vertauschungen nötig waren, um die jeweilige Permutation zu erzeugen (gerade oder ungerade Anzahl).
Beispiel
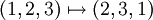 zwei Vertauschungen und somit gerade
zwei Vertauschungen und somit gerade 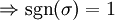
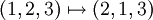 eine Vertauschung und somit ungerade
eine Vertauschung und somit ungerade 
Diese Formel enthält n! Summanden und ist somit unhandlich, falls n größer als 3 ist. Sie eignet sich jedoch zum Beweis von Aussagen über Determinanten.
Gauß-Algorithmus zur Determinantenberechnung
Im Allgemeinen können Determinanten mit dem Gauß-Algorithmus unter Verwendung der folgenden Regeln berechnet werden:
- Falls A eine obere (untere) Dreiecksmatrix ist, also ai,j = 0 für j < i (nur Nullen unterhalb (oberhalb) der Hauptdiagonalen), dann ist
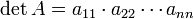 das Produkt der Hauptdiagonal-Einträge
das Produkt der Hauptdiagonal-Einträge
- Falls B sich aus A ergibt, indem man zwei Zeilen oder Spalten vertauscht, dann ist detB = − detA
- Falls B sich aus A ergibt, indem man ein Vielfaches einer Zeile oder Spalte zu einer anderen Zeile oder Spalte addiert, dann ist detB = detA.
- Falls B sich aus A ergibt, indem man ein Vielfaches c einer Zeile oder Spalte bildet, dann ist
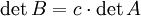 .
.
Beginnend mit einer beliebigen quadratischen Matrix benutzt man die letzten drei dieser vier Regeln, um die Matrix in eine obere Dreiecksmatrix zu überführen, und berechnet dann die Determinante als Produkt der Diagonalelemente.
Auf diesem Prinzip basiert auch die Determinantenberechnung mittels der LR-Zerlegung. Da sowohl L als auch R Dreiecksmatrizen sind, ergeben sich ihre Determinanten aus dem Produkt der Diagonalelemente, die bei L alle auf 1 normiert sind. Gemäß der Produktregel ergibt sich die Determinante damit aus dem Zusammenhang
Laplacescher Entwicklungssatz
Mit dem laplaceschen Entwicklungssatz kann man die Determinante einer
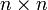 -Matrix „nach einer Zeile oder Spalte entwickeln“. Die beiden Formeln lauten
-Matrix „nach einer Zeile oder Spalte entwickeln“. Die beiden Formeln lauten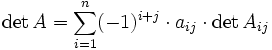 (Entwicklung nach der j-ten Spalte)
(Entwicklung nach der j-ten Spalte)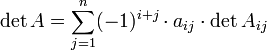 (Entwicklung nach der i-ten Zeile)
(Entwicklung nach der i-ten Zeile)
wobei Aij die
 -Untermatrix von A ist, die durch Streichen der i-ten Zeile und j-ten Spalte entsteht. Das Produkt ( − 1)i + jdetAij wird Cofaktor
-Untermatrix von A ist, die durch Streichen der i-ten Zeile und j-ten Spalte entsteht. Das Produkt ( − 1)i + jdetAij wird Cofaktor 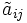 genannt.
genannt.Genau genommen gibt der Entwicklungssatz nur ein Verfahren an, die Summanden der Leibniz-Formel in einer bestimmten Reihenfolge zu berechnen. Dabei wird die Determinante bei jeder Anwendung um eine Dimension reduziert. Falls gewünscht, kann das Verfahren so lange angewandt werden, bis sich ein Skalar ergibt. Der Laplace’sche Entwicklungssatz ist bei kleinen Matrizen und Matrizen mit vielen Nullen sehr effizient. Ein Beispiel ist
(Entwicklung nach der ersten Zeile)
Der Laplacesche Entwicklungssatz lässt sich auf folgende Weise verallgemeinern. Statt nur nach einer Zeile oder Spalte kann man auch nach mehreren Zeilen oder Spalten entwickeln. Die Formel dafür lautet
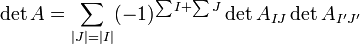 ,
,
mit den folgenden Bezeichnungen: I und J sind Teilmengen von
 und AIJ ist die Untermatrix von A, die aus den Zeilen mit den Indizes aus I und den Spalten mit den Indizes aus J besteht. I' und J' bezeichnen die Komplemente von I und J.
und AIJ ist die Untermatrix von A, die aus den Zeilen mit den Indizes aus I und den Spalten mit den Indizes aus J besteht. I' und J' bezeichnen die Komplemente von I und J. 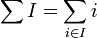 ist die Summe der Indizes aus I. Für die Entwicklung nach den Zeilen mit den Indizes aus I läuft die Summe über alle
ist die Summe der Indizes aus I. Für die Entwicklung nach den Zeilen mit den Indizes aus I läuft die Summe über alle 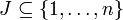 , wobei die Anzahl dieser Spaltenindizes | J | gleich der Anzahl der Zeilen | I | ist, nach denen entwickelt wird. Für die Entwicklung nach den Spalten mit den Indizes aus J läuft die Summe über I. Die Anzahl der Summanden ergibt sich als der Binomialkoeffizient
, wobei die Anzahl dieser Spaltenindizes | J | gleich der Anzahl der Zeilen | I | ist, nach denen entwickelt wird. Für die Entwicklung nach den Spalten mit den Indizes aus J läuft die Summe über I. Die Anzahl der Summanden ergibt sich als der Binomialkoeffizient  mit k = | I | = | J | .
mit k = | I | = | J | .Determinante eines Endomorphismus
Es sei V ein n-dimensionaler Vektorraum über einem Körper K. (Allgemeiner kann man auch einen kommutativen Ring K mit Einselement und einem freien Modul vom Rang n über K betrachten.)
Die Determinante einer K-linearen Abbildung
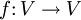 ist die Determinante einer Darstellungsmatrix von f bezüglich einer Basis von V. Sie hängt nicht von der Wahl dieser Basis ab.
ist die Determinante einer Darstellungsmatrix von f bezüglich einer Basis von V. Sie hängt nicht von der Wahl dieser Basis ab.Eine alternative Definition ist die folgende: Es sei
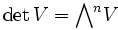 und
und 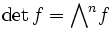 . Dann ist detV ein eindimensionaler K-Vektorraum (bzw. ein freier K-Modul vom Rang 1), also kann die lineare Abbildung
. Dann ist detV ein eindimensionaler K-Vektorraum (bzw. ein freier K-Modul vom Rang 1), also kann die lineare Abbildungmit einem Element von K identifiziert werden; dieses Element ist die Determinante von f.
Eigenschaften
Produktregel
Die Determinante ist eine multiplikative Abbildung in dem Sinne, dass
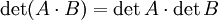 für alle
für alle 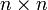 -Matrizen A und B.
-Matrizen A und B.
Das bedeutet, dass die Abbildung
 ein Gruppenhomomorphismus von der allgemeinen linearen Gruppe in die Einheitengruppe K * des Körpers ist. Der Kern dieser Abbildung ist die spezielle lineare Gruppe. Allgemeiner gilt für die Determinante einer quadratischen Matrix, welche das Produkt zweier (nicht notwendig quadratischer) Matrizen ist, der Satz von Binet-Cauchy.
ein Gruppenhomomorphismus von der allgemeinen linearen Gruppe in die Einheitengruppe K * des Körpers ist. Der Kern dieser Abbildung ist die spezielle lineare Gruppe. Allgemeiner gilt für die Determinante einer quadratischen Matrix, welche das Produkt zweier (nicht notwendig quadratischer) Matrizen ist, der Satz von Binet-Cauchy.Noch allgemeiner ergibt sich als unmittelbare Folgerung aus dem Satz von Binet-Cauchy eine Formel für die Berechnung eines Minors der Ordnung k eines Produktes zweier Matrizen. Ist A eine
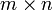 -Matrix und B eine
-Matrix und B eine  -Matrix und ist
-Matrix und ist 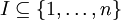 und
und 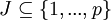 mit | I | = | J | = k, dann gilt mit den Bezeichnungen wie beim verallgemeinerten Entwicklungssatz
mit | I | = | J | = k, dann gilt mit den Bezeichnungen wie beim verallgemeinerten Entwicklungssatz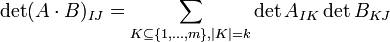 ,
,
Der Fall m = p = k liefert den Satz von Binet-Cauchy (welcher für n=m zur gewöhnlichen Produktregel wird) und der Spezialfall k = 1 liefert die Formel für die gewöhnliche Matrizenmultiplikation.
Multiplikation mit Skalaren
Es ist einfach zu sehen, dass
 und somit
und somit- det(rA) = rndetA für alle
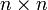 Matrizen A und alle Skalare r.
Matrizen A und alle Skalare r.
Inverses
Falls A invertierbar ist, dann ist
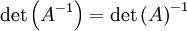 .
.Transponierte Matrix
Eine Matrix und ihre Transponierte haben dieselbe Determinante
- detA = detAT.
Ähnliche Matrizen
Falls A und B ähnlich sind, d.h. falls eine invertierbare Matrix X existiert, so dass
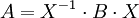 , dann ist mit der Multiplikativität
, dann ist mit der Multiplikativität- detA = detB.
Deswegen kann man die Determinante einer linearen Abbildung
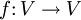 definieren (wobei V ein endlich-dimensionaler Vektorraum ist), indem man eine Basis für V wählt, f als Matrix relativ zu dieser Basis beschreibt und die Determinante dieser Matrix nimmt. Das Ergebnis ist unabhängig von der gewählten Basis.
definieren (wobei V ein endlich-dimensionaler Vektorraum ist), indem man eine Basis für V wählt, f als Matrix relativ zu dieser Basis beschreibt und die Determinante dieser Matrix nimmt. Das Ergebnis ist unabhängig von der gewählten Basis.Es gibt Matrizen, die die gleiche Determinante haben, aber nicht ähnlich sind.
Blockmatrizen
Für die Determinante einer
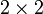 -Blockmatrix
-Blockmatrixmit quadratischen Blöcken A und D kann man unter gewissen Voraussetzungen Formeln angeben, welche die Blockstruktur ausnutzen. Für B = 0 oder C = 0 gilt:
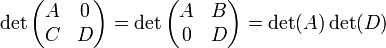 .
.
Ist A invertierbar, so folgt aus der Zerlegung
die Formel
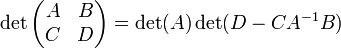 .
.
Im Spezialfall, dass alle vier Blöcke die gleiche Größe haben und paarweise kommutieren, ergibt sich daraus mit Hilfe der Produktregel
 .
.
Dabei bezeichne
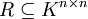 einen kommutativen Unterring des Ringes aller
einen kommutativen Unterring des Ringes aller 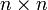 -Matrizen mit Einträgen aus dem Körper K, so dass
-Matrizen mit Einträgen aus dem Körper K, so dass  (zum Beispiel den von diesen vier Matrizen erzeugten Unterring), und
(zum Beispiel den von diesen vier Matrizen erzeugten Unterring), und 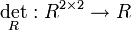 sei die entsprechende Abbildung, die einer quadratischen Matrix mit Einträgen aus R ihre Determinante zuordnet. Diese Formel gilt auch, falls A nicht invertierbar ist und verallgemeinert sich für Matrizen aus
sei die entsprechende Abbildung, die einer quadratischen Matrix mit Einträgen aus R ihre Determinante zuordnet. Diese Formel gilt auch, falls A nicht invertierbar ist und verallgemeinert sich für Matrizen aus 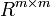 .[1]
.[1]Eigenwerte
Die Determinate einer
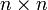 -Matrix A über den reellen oder komplexen Zahlen mit den Eigenwerten
-Matrix A über den reellen oder komplexen Zahlen mit den Eigenwerten 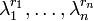 (wobei ri die algebraische Vielfachheit zum Eigenwert λi ist) kann mittels
(wobei ri die algebraische Vielfachheit zum Eigenwert λi ist) kann mittelsberechnet werden.
Ableitung
Die Determinante von reellen quadratischen Matrizen fester Dimension n ist eine Polynomfunktion
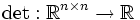 und als solche überall differenzierbar. Ihre Ableitung kann mit Hilfe von Jacobis Formel dargestellt werden:
und als solche überall differenzierbar. Ihre Ableitung kann mit Hilfe von Jacobis Formel dargestellt werden:wobei
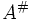 die zu A komplementäre Matrix bezeichnet. Insbesondere ergibt sich für invertierbares A, dass
die zu A komplementäre Matrix bezeichnet. Insbesondere ergibt sich für invertierbares A, dassoder vereinfacht,
falls die Werte der Matrix X hinreichend klein sind. Der Spezialfall wenn A gleich der Einheitsmatrix E ist, ergibt
Verallgemeinerungen
Es ist sinnvoll, die Determinante für Matrizen zu definieren, deren Einträge in einem kommutativen Ring liegen. Die Regeln zur Berechnung, die Leibniz-Formel und die Kompatibilität mit der Matrix-Multiplikation bleiben gültig, mit der Ausnahme, dass nun eine Matrix A genau dann invertierbar ist, falls detA ein invertierbares Element des zugrundeliegenden Ringes ist.
Für manche Zwecke betrachtet man auch formale Determinanten, deren Einträge sowohl Skalare als auch Vektoren sind, z.B. bei der Definition eines verallgemeinerten Kreuzprodukts. Diese werden mit der Leibniz-Formel berechnet (selbstverständlich dürfen dabei keine Vektoren miteinander multipliziert werden).
Man kann die Determinante wie folgt abstrakt als eine gewisse antisymmetrische multilineare Abbildung definieren: Falls R ein kommutativer Ring ist und M = Rn der n-dimensionale freie R-Modul, dann ist
die eindeutig bestimmte Abbildung mit den folgenden Eigenschaften:
- det ist R-linear in jedem der n Argumente.
- det ist antisymmetrisch, d.h. falls zwei der n Argumente gleich sind, so ist die Determinante Null.
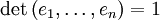 , wobei ei das Element von M ist, das eine 1 als i-te Koordinate hat und sonst Nullen.
, wobei ei das Element von M ist, das eine 1 als i-te Koordinate hat und sonst Nullen.
Ähnliche Begriffe
Die Permanente ist ein „vorzeichenloses“ Analogon zur Determinante, wird allerdings viel seltener verwendet.
Siehe auch
- Determinantenfunktion
- Wronski-Determinante
- Pfaffsche Determinante
- Vandermonde-Determinante
- Gramsche Determinante
- Funktionaldeterminante (Jacobi-Determinante)
Einzelnachweise
- ↑ John R. Silvester: Determinants of Block Matrices. In: The Mathematical Gazette. Vol. 84, No. 501 (November 2000), S. 460-467 (PDF; 148KB).
Weblinks
- Eigenschaften, Berechnung der Determinante, Beweise (pdf)
- Die Determinantenfunktion (pdf)
- Online-Tool zum Berechnen von Determinanten
- Determinantengesetze (pdf) (Prof. Dr. Weber TU Dresden) - 15 Rechengesetze für Determinanten (alle mit Beweis) mit Beispielen
Wikimedia Foundation.