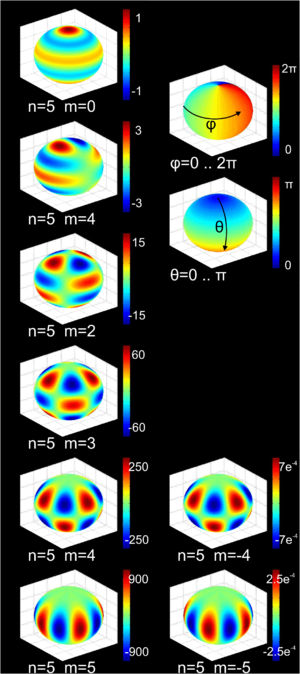
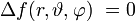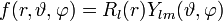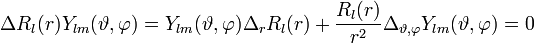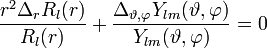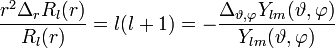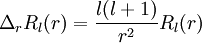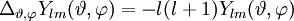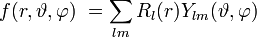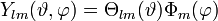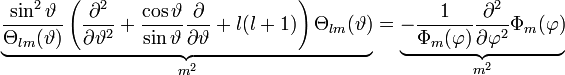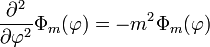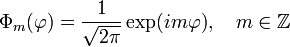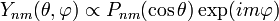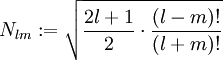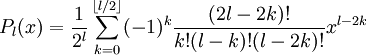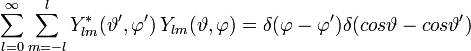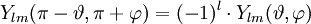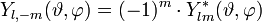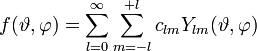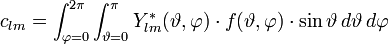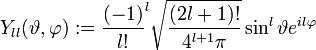- Kugelfunktionen
-
Die Kugelflächenfunktionen sind ein vollständiger und orthonormaler Satz von Eigenfunktionen des Winkelanteils des Laplace-Operators. Dieser Winkelanteil zeigt sich, wenn der Laplace-Operator in Kugelkoordinaten geschrieben wird. Die Eigenwertgleichung lautet:
Die Eigenfunktionen sind die Kugelflächenfunktionen, dabei sind Nlm Normierungsfaktoren und Plm(z) die zugeordneten Legendrepolynome (Details siehe unten):
Besonders in der theoretischen Physik haben die Kugelflächenfunktionen eine große Bedeutung für die Lösung partieller Differentialgleichungen. Sie treten zum Beispiel bei der Berechnung von Atomorbitalen auf, da die beschreibende zeitunabhängige Schrödingergleichung den Laplace-Operator enthält und sich das Problem am besten in Kugelkoordinaten lösen lässt. Auch die in der Elektrostatik auftretenden Randwertprobleme können elegant durch die Entwicklung nach Kugelflächenfunktionen gelöst werden. In der Geophysik und Geodäsie werden die Kugelflächenfunktionen bei der Approximation des Geoids verwendet.
Inhaltsverzeichnis
Zusammenhang mit dem Laplace-Operator
Der Winkelanteil des Laplace-Operators zeigt sich, wenn dieser in Kugelkoordinaten geschrieben wird:
Der rechte, eingeklammerte Teil wird hier als Winkelanteil
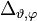 bezeichnet. Er ist direkt proportional zum Quadrat des Drehimpulsoperators
bezeichnet. Er ist direkt proportional zum Quadrat des Drehimpulsoperators 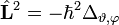 .
.Die Laplacesche Differentialgleichung in Kugelkoordinaten
hat neben der trivialen Lösung, f = 0, verschiedenste Lösungen mit vielen technischen Anwendungen.
Zur Lösung wird folgender Produktansatz verwendet, wobei Rl(r) nur vom Radius und
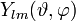 nur von Polar- und Azimutwinkel abhängt:
nur von Polar- und Azimutwinkel abhängt:Ergibt eingesetzt:
Multiplikation von r2 und Division durch
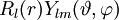 liefert:
liefert:Diese Gleichung kann nur erfüllt werden, wenn in beiden Summanden unabhängig voneinander Radius und Winkel variierbar sind. Beide Summanden müssen somit denselben konstanten Wert annehmen, der zu l(l + 1) gewählt wird (diese Festlegung erweist sich später als sinnvoll):
Durch dieses Verfahren, welches Separation der Variablen genannt wird, wurde also das ursprüngliche Problem, nämlich die Lösung der Laplace-Gleichung (partielle Differentialgleichung mit drei unabhängigen Variablen), auf das einfachere Problem der Lösung einer gewöhnlichen Differentialgleichung (Radialgleichung)
und einer partiellen Differentialgleichung mit zwei unabhängigen Variablen (winkelabhängige Gleichung) reduziert.
Nun lässt sich aufgrund der Orthogonalität und Vollständigkeit der Kugelflächenfunktionen zeigen, dass sich jede quadratintegrable Funktion aus diesen speziellen Funktionen als Summe zusammensetzen lässt:
Aufgrund der Linearität des Laplace-Operators lassen sich also durch Addition der Lösungen der Radialgleichung, multipliziert mit den Kugelflächenfunktionen, beliebig viele Lösungen der Laplace-Gleichung konstruieren. Damit ergibt sich automatisch eine Darstellung des Lösungsraumes der Laplace-Gleichung.
Die Kugelfunktionen wurden besonders von Legendre (Kugelfunktionen erster Art), Laplace (Kugelfunktionen zweiter Art) und Franz Neumann (Kugelfunktionen mit mehreren Veränderlichen) behandelt.
Lösung der Eigenwertgleichung
Die Eigenwertgleichung
wird mit folgenden Produktansatz separiert:
Umsortieren liefert:
Um beide Seite getrennt voneinander variieren zu können, müssen beide Seiten den gleichen konstanten Wert annehmen. Diese Separationskonstante wird als m2 gewählt. Es ergeben sich zwei gewöhnliche Differentialgleichungen, die Polargleichung
und die Azimutalgleichung.
Die Azimutalgleichung wird durch
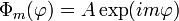 gelöst, wobei die m wegen der Zusatzbedingung der Eindeutigkeit auf der Kugeloberfläche
gelöst, wobei die m wegen der Zusatzbedingung der Eindeutigkeit auf der Kugeloberfläche 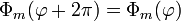 eingeschränkt sind auf ganze Zahlen exp(im2π) = 1. Mit
eingeschränkt sind auf ganze Zahlen exp(im2π) = 1. Mit 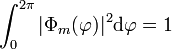 erhält man die normierte Lösung der Azimutalgleichung:
erhält man die normierte Lösung der Azimutalgleichung:Die Polargleichung kann mit einem Potenzreihenansatz gelöst werden. Die Lösungen sind nur dann endlich, eindeutig und stetig, wenn
 .
.
Dann sind die Lösungen die zugeordneten Legendrepolynome
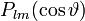 und mit
und mit 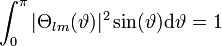 erhält man die normierte Lösung der Polargleichung:
erhält man die normierte Lösung der Polargleichung:Die Gesamtlösung des Winkelanteils ist das Produkt aus den beiden erhaltenen Lösungen, nämlich die Kugelflächenfunktionen.
Darstellung
Die Darstellung der Kugelflächenfunktionen
 ergibt sich als Lösung der oben genannten Eigenwertgleichung. Die konkrete Rechnung liefert:
ergibt sich als Lösung der oben genannten Eigenwertgleichung. Die konkrete Rechnung liefert:Dabei sind
die zugeordneten Legendrepolynome und
sind Normierungsfaktoren. Mitunter ist die Berechnung über:
mit
vorteilhafter (
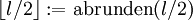 ), da l-faches Ableiten entfällt.
), da l-faches Ableiten entfällt.Eine andere Definition geht über homogene, harmonische Polynome. Diese sind durch ihren Wert auf der Sphäre eindeutig bestimmt. Jedes homogene harmonische Polynom vom Grad n lässt sich als Linearkombination von Kugelflächenfunktionen multipliziert mit rn schreiben und umgekehrt. Wählt man beispielsweise die Funktion, die konstant 1 ist, als Basis des eindimensionalen Vektorraumes der 0-homogenen harmonischen Polynome und x, y und z als Basis des dreidimensionalen Vektorraumes der 1-homogenen, so erhält man in Kugelkoordinaten nach Division von rn die Funktionen
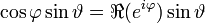 ,
,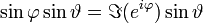 ,
,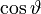 .
.
Für die homogenen Polynome vom Grad 2 erkennt man in der Liste unten schnell auch die Terme
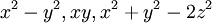 wieder, nur mit einem falschen Vorfaktor.
wieder, nur mit einem falschen Vorfaktor.Eigenschaften
Die Kugelflächenfunktionen haben folgende Eigenschaften:
- Orthogonalitätsrelation: (δij ist das Kronecker-Delta)
- Vollständigkeit: (δ(x) ist die Delta-Distribution)
- Parität: Der Übergang
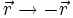 sieht in Kugelkoordinaten folgendermaßen aus:
sieht in Kugelkoordinaten folgendermaßen aus: 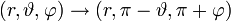 . Unter dieser Transformation verhalten sich die Kugelflächenfunktionen wie folgt:
. Unter dieser Transformation verhalten sich die Kugelflächenfunktionen wie folgt:
- Komplexe Konjugation: Die jeweiligen Yl, − m erhält man aus den Ylm durch:
Entwicklung nach Kugelflächenfunktionen
Die Kugelflächenfunktionen bilden ein vollständiges Funktionensystem. Daher können alle quadratintegrablen Funktionen
 (mit
(mit 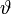 und
und 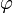 im Sinne der Kugelkoordinaten) nach den Kugelflächenfunktionen entwickelt werden:
im Sinne der Kugelkoordinaten) nach den Kugelflächenfunktionen entwickelt werden:Die Entwicklungskoeffizienten clm berechnen sich zu:
Dabei ist
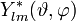 das komplex-konjugierte zu
das komplex-konjugierte zu 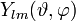 . Die Darstellung einer Funktion f(x) mit sin- und cos-Funktion als Fourierreihe ist ein Analogon zur Entwicklung einer zweidimensionalen Funktion
. Die Darstellung einer Funktion f(x) mit sin- und cos-Funktion als Fourierreihe ist ein Analogon zur Entwicklung einer zweidimensionalen Funktion  mit
mit 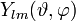 auf einer Kugeloberfläche.
auf einer Kugeloberfläche.Die ersten Kugelflächenfunktionen
Die ersten Kugelflächenfunktionen Ylm l = 0 l = 1 l = 2 l = 3 m = -3 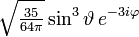
m = −2 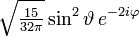
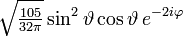
m = −1 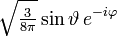
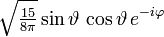
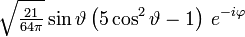
m = 0 
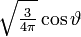
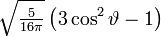
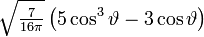
m = 1 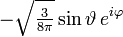

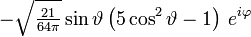
m = 2 
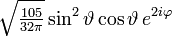
m = 3 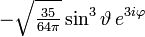
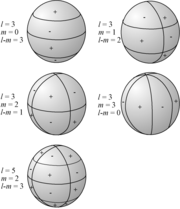
Nomenklatur in der Geophysik
Kugelflächenfunktion werden auch gerne in der Geophysik verwendet. Man unterscheidet hier zwischen:
- zonal (m = 0): unabhängig von Längengrad
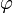
- sektoriell (m = l):
- tesseral (sonst): längen- und breitengradabhängig
Literatur
- Eduard Heine Handbuch der Kugelfunctionen Georg Reimer, Berlin, 1861.
- A. Wangerin Theorie Des Potentials Und Der Kugelfunktionen II Band Walter de Gruyter, Berlin, 1921. (University of Michigan)
- Claude Cohen-Tannoudji, Bernard Diu und Franck Laloë: Quantenmechanik 1. 2. Auflage, Walter de Gruyter, Berlin - New York 1999, S. 649 ff.
- Torsten Fließbach: Elektrodynamik. 4. Auflage, Spektrum, München 2005, S. 99 ff.
- Otto Forster: Analysis 3. 3. Auflage, Vieweg Studium, 1984
Weblinks
Wikimedia Foundation.



![Y_{lm}:\;\left[0,\pi\right]\times\left[0,2\pi\right]\rightarrow\mathbb{C},\quad(\vartheta,\varphi)\mapsto\frac{1}{\sqrt{2\pi}}\, N_{lm}\, P_{lm}(\cos\vartheta)\, e^{im\varphi} \quad \text{mit}\quad N_{lm} := \sqrt{\tfrac{2l+1}{2}\,\tfrac{(l-m)!}{(l+m)!}}](/pictures/dewiki/54/6151a04e48203332beedcc4fd4ef28a2.png)