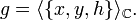Lie-Algebra sl

In der Mathematik ist die Lie-Algebra sl(2,C) der Prototyp einer einfachen Lie-Algebra. Die sl(2,C) ist eine dreidimensionale, komplexe, einfache Lie-Algebra. Durch diese Eigenschaften ist sie als Lie-Algebra bereits eindeutig identifiziert.

Bei der Klassifikation der endlichdimensionalen halbeinfachen Lie-Algebra hat sie die Funktion einer Testalgebra. Man kann sich (dieser Vergleich ist nicht so ganz richtig) jede halbeinfache Lie-Algebra zusammengesetzt aus sl(2,C) denken.

In der Physik ist die sl(2,C) die Lie-Algebra, die die Lorentzgruppe erzeugt. Sie spielt dort in der speziellen Relativitätstheorie eine entscheidende Rolle.

Es gibt viele Bezeichnungen und Realisationen der sl(2,C), die im Folgenden beschrieben werden.

Definition durch Kommutator-Relationen

Betrachten wir den dreidimensionalen, komplexen Vektorraum g, der durch die Basis x, y, z erzeugt wird:

$g=\langle \{x,y,h\} \rangle_{\mathbb C}.$

Durch die folgenden Relationen wird auf g eine Lie-Algebra-Struktur definiert:

$[x,y]=h \;\;\;\; [h,x]=2x \;\;\;\; [h,y]=-2y$

Als 2x2-Matrizen

Betrachten wir alle 2x2-Matrizen deren Spur verschwindet. Setzen wir

$x= \begin{pmatrix}0&1\\ 0 & 0\end{pmatrix} \;\;\;\; y=\begin{pmatrix}0&0\\ 1 & 0\end{pmatrix} \;\;\; \;\;\;\; h=\begin{pmatrix}1&0\\ 0 & -1\end{pmatrix}$

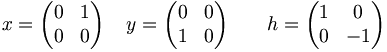
so haben wir mit der Kommutatorklammer die Relationen

$[x,y]=h \;\;\;\; [h,x]=2x \;\;\;\; [h,y]=-2y$

Kreuzprodukt auf C³

Auf dem 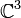${\mathbb C}^3$ bildet das Kreuzprodukt eine Lie-Algebra. Setzen wir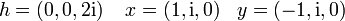

$h=(0,0,2\mathrm i)\;\;\;\; x=(1,\mathrm i,0)\;\;\; y=(-1,\mathrm i,0)$

so haben wir die obigen Kommutator-Relationen.

$h \times x = 2x \;\;\;\; h \times y = -2y \;\;\;\; x\times y = h$

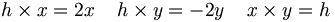
Reelle Formen der sl(2,C)

Die Lie-Algebra sl(2,C) hat zwei reelle Formen. Eine reelle Form einer Lie-Algebra ist eine reelle Lie-Algebra, die, wenn man sie komplexifiziert, die ursprüngliche Lie-Algebra ergibt (hier sl(2,C)). Die beiden reellen Formen der sl(2,C) sind die Lie-Algebra su(2) und die Lie-Algebra sl(2,R).