Load Balancing Problem

Das Lastverteilungsproblem (Load Balancing Problem) beschäftigt sich mit den theoretischen Aspekten der Lastverteilung. Es wird dazu angenommen, dass jeder Job von jeder Maschine erfüllt werden kann, und dass alle Jobs und Maschinen bereits im Voraus bekannt sind. So kann eine optimale Verteilung der Jobs berechnet werden, wobei die Höchstlaufzeit aller Maschinen möglichst gering bleibt.

Formale Beschreibung

Es stehen m Maschinen $M_1 \ldots M_m$zur Verfügung. Auf diese Maschinen sollen n Jobs $j_1 \ldots j_n$ verteilt werden, wobei die Länge eines Jobs j mit t_j bezeichnet wird.
Das Ziel ist eine Verteilung der Jobs auf die Maschinen, so dass die Gesamtlaufzeit möglichst gering wird; es ist also die Laufzeit der am längsten arbeitenden Maschine zu minimieren, denn sie ist für die Gesamtlaufzeit ausschlaggebend.

NP-Vollständigkeit des Entscheidungsproblems

Das entsprechende Entscheidungsproblem fragt: Gibt es eine Lastverteilung, so dass die Gesamtlaufzeit höchstens T ist?

Formal: 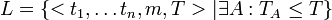$L = \{<t_1, \ldots t_n, m, T> | \exists A: T_A \leq T\}$, wobei T_A eine Verteilung der Jobs ist.

Um zu zeigen, dass L NP-vollständig ist, sind zwei Punkte zu beweisen:

1. L liegt in NP. Dazu muss ein Zeuge (eine Lösung) angegeben werden können, welcher in Polynomialzeit verifiziert werden kann. Dieser Zeuge ist die konkrete Verteilung der Jobs auf die Maschinen; es ist dann in Polynomialzeit verifizierbar, dass die vorgegebene Höchstlaufzeit eingehalten wird.
2. L ist mindestens so schwierig wie alle anderen Sprachen in NP. Dazu genügt es, L auf ein anderes Problem aus NP zurückzuführen, hier auf das Binärpartitionsproblem BINPART. Es ist zu zeigen, dass man jede Eingabe für BINPART in eine Eingabe für das Lastverteilungsproblem umwandeln kann:
   

Sei 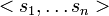$<s_1, \ldots s_n>$ eine Eingabemenge von Zahlen für BINPART. Wähle dann als Eingabemenge für das Lastverteilungsproblem $<s_1, \ldots s_n, 2, \sum^n_{j=1}\frac{s_j}{2}>$.

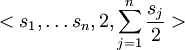• Wenn BINPART eine Lösung hat (d.h. es existiert eine Aufteilung von 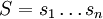$S = s_1 \ldots s_n$ in zwei Partitionen, so dass die Summe der Zahlen in beiden Partitionen gleich ist), dann hat auch das Lastverteilungsproblem auf die veränderte Eingabe eine Lösung. Dazu wird die gefundene Aufteilung direkt auf die zwei zur Verfügung stehenden Maschinen angewendet, so dass beide Maschinen genau gleich lange laufen. Somit erhält jede der beiden Maschinen genau die Hälfte der Gesamtlaufzeit aller Jobs, es existiert also tatsächlich eine Lösung mit $\sum^n_{j=1}\frac{s_j}{2}=T$.
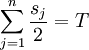• Wenn BINPART keine Lösung hat (d.h. es existiert keine Aufteilung von 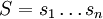$S = s_1 \ldots s_n$ in zwei Partitionen, so dass die Summe der Zahlen in beiden Partitionen gleich ist), dann hat auch das Lastverteilungsproblem auf die veränderte Eingabe keine Lösung. Dazu wird die gefundene Aufteilung direkt auf die zwei zur Verfügung stehenden Maschinen angewendet. Da keine gleichmäßige Aufteilung der Zahlen gefunden werden konnte, muss eine der beiden Maschinen länger als die andere laufen. Somit hat eine der beiden Maschinen eine längere Laufzeit als die Hälfte der Gesamtlaufzeit aller Jobs, also ist T ausreichend klein gewählt worden, um eine Lösung unmöglich zu machen.

Approximation durch Greedy-Algorithmus

Greedy-Balance

Algorithmus

Der nächste Job wird genau der Maschine zugewiesen, die bis jetzt die geringste Laufzeit hatte.

Analyse

Es kann leicht ein Beispiel dafür gefunden werden, dass dieser Algorithmus nicht die optimale Lösung liefert - jedoch wird eine 2-Approximation erreicht: Sei M_i die Maschine, die den zuletzt verteilten Job j erhalten hat. Dann galt für diese Maschine vorher, dass sie die bisher kleinste Laufzeit hatte, das heißt insbesondere, dass ihre Laufzeit kleiner als die durchschnittliche Laufzeit aller Maschinen war.
Diesen Durchschnitt kann man angeben als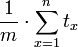 $\frac{1}{m} \cdot \sum^n_{x=1} t_x$.

Sei nun bei optimaler Verteilung der Jobs T* die bestmögliche Gesamtlaufzeit. Ohne dass man etwas genaues über T* weiß, kann man trotzdem die beiden Abschätzungen treffen:

• T* ist mindestens so lang wie der längste Job: $T^* \geq MAX(t_x)$.
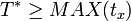• T* ist mindestens so lang wie die völlig gleichmäßige Verteilung der Jobs, falls dies möglich wäre: $T^* \geq \frac{1}{m} \cdot \sum^n_{x=1} t_x$.

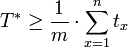Kombiniert man diese Abschätzungen, so erhält man für die greedy ermittelte Lösung T:

$T = T_{M_i} = (T_{M_i} - t_j) + (t_j) \leq \left(\frac{1}{m} \cdot \sum^n_{x=1} t_x\right) + (T^*) \leq 2 \cdot T^*$.

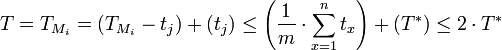Sorted-Balance

Sortiert man die Jobs im Vorfeld und verteilt sie absteigend nach Länge auf die Maschinen, so gilt außerdem für den zuletzt hinzugefügten Job j:

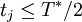• $t_j \leq T^* / 2$. Der Grund dafür ist, daß bei einer Maschine, welche mindestens zwei Jobs bearbeitet, der jeweils nächstfolgende kürzer als der vorangehende ist. So kann der zuletzt hinzugefügte Job auch nur höchstens die Hälfte der nötigen Gesamtzeit der am längsten laufenden Maschine ausmachen (er kann nicht größer als ein bereits vorhandener sein).

In diesem Fall kann also die Abschätzung verbessern auf:

$T = T_{M_i} = (T_{M_i} - t_j) + (t_j) \leq \left(\frac{1}{m} \cdot \sum^n_{x=1} t_x\right) + (T^*/2) \leq 1,5 \cdot T^*$.

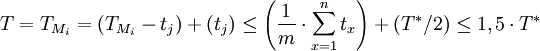Literatur

• Jon Kleinberg, Éva Tardos. Algorithm Design. Pearson International Edition, 2006. ISBN 0-321-37291-3. Seiten 600ff.