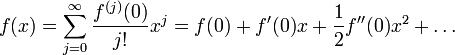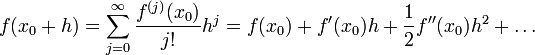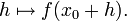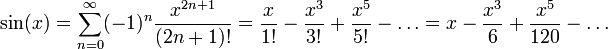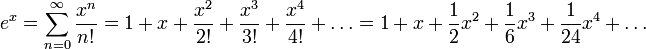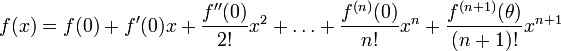MacLaurinsche Reihe — Die Maclaurinsche Reihe (nach Colin Maclaurin) ist in der Analysis eine Bezeichnung für den Spezialfall einer Taylor Reihe mit Entwicklungsstelle 0: Durch eine geeignete Substitution kann man jede Taylorreihe als Maclaurinreihe auffassen: ist die … Deutsch Wikipedia
Maclaurin-Reihe — Die Maclaurinsche Reihe (nach Colin Maclaurin) ist in der Analysis eine Bezeichnung für den Spezialfall einer Taylor Reihe mit Entwicklungspunkt 0: Durch eine geeignete Substitution kann man jede Taylorreihe als Maclaurinreihe auffassen: ist die… … Deutsch Wikipedia
Colin MacLaurin — (* Februar 1698 in Kilmodan; † 14. Juni 1746 in Edinburgh) war ein schottischer Mathematiker. Maclaurin wurde mit 19 Jahren Professor in Aberdeen und ab 1726 in Edinburgh. Er verfasste 1742 sein wichtigstes Werk A treatise of fluxions und war… … Deutsch Wikipedia
Collin MacLaurin — Colin Maclaurin Colin Maclaurin (* Februar 1698 in Kilmodan; † 14. Juni 1746 in Edinburgh) war ein schottischer Mathematiker. Maclaurin wurde mit 19 Jahren Professor in Aberdeen und ab 1726 in Edinburgh. Er verfasste 1742 sein wichtigstes Werk A… … Deutsch Wikipedia
Maclaurin — Colin Maclaurin Colin Maclaurin (* Februar 1698 in Kilmodan; † 14. Juni 1746 in Edinburgh) war ein schottischer Mathematiker. Maclaurin wurde mit 19 Jahren Professor in Aberdeen und ab 1726 in Edinburgh. Er verfasste 1742 sein wichtigstes Werk A… … Deutsch Wikipedia
Taylor-Entwicklung — In der Analysis verwendet man Taylorreihen (auch Taylor Entwicklungen oder Taylor Näherung), um Funktionen in der Umgebung bestimmter Punkte durch Potenzreihen darzustellen. So kann ein komplizierter analytischer Ausdruck durch eine nach wenigen… … Deutsch Wikipedia
Taylor-Näherung — In der Analysis verwendet man Taylorreihen (auch Taylor Entwicklungen oder Taylor Näherung), um Funktionen in der Umgebung bestimmter Punkte durch Potenzreihen darzustellen. So kann ein komplizierter analytischer Ausdruck durch eine nach wenigen… … Deutsch Wikipedia
Taylor-Reihe — In der Analysis verwendet man Taylorreihen (auch Taylor Entwicklungen oder Taylor Näherung), um Funktionen in der Umgebung bestimmter Punkte durch Potenzreihen darzustellen. So kann ein komplizierter analytischer Ausdruck durch eine nach wenigen… … Deutsch Wikipedia
Taylorapproximation — In der Analysis verwendet man Taylorreihen (auch Taylor Entwicklungen oder Taylor Näherung), um Funktionen in der Umgebung bestimmter Punkte durch Potenzreihen darzustellen. So kann ein komplizierter analytischer Ausdruck durch eine nach wenigen… … Deutsch Wikipedia
Taylorentwicklung — In der Analysis verwendet man Taylorreihen (auch Taylor Entwicklungen oder Taylor Näherung), um Funktionen in der Umgebung bestimmter Punkte durch Potenzreihen darzustellen. So kann ein komplizierter analytischer Ausdruck durch eine nach wenigen… … Deutsch Wikipedia
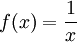 oder
oder 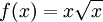 -, lässt sich keine Maclaurinsche Reihe entwickeln.
-, lässt sich keine Maclaurinsche Reihe entwickeln.