Markoff-Ungleichung

In der Wahrscheinlichkeitstheorie gibt die Markow-Ungleichung (nach Andrei Andrejewitsch Markow) eine obere Schranke für die Wahrscheinlichkeit an, dass eine Zufallsvariable größer einer positiven Konstante ist.

Satz

Sei (Ω,σ(Ω),P) ein Wahrscheinlichkeitsraum und 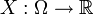$X:\Omega \rightarrow \mathbb{R}$ eine reele Zufallsvariable und a eine positive, reellwertige Konstante und ferner 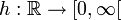$h:\mathbb{R} \rightarrow [0,\infty[$ monoton wachsende Funktion. Die allgemeine Markow-Ungleichung besagt dann:

$P \left[ X \geq a \right] \leq \frac{\textrm{E}\left[h(X)\right]}{h(a)}.$

Beweis

Sei I_A(x) die charakteristische Funktion der Menge A. Dann gilt:

$P \left[ X \geq a \right] = \int I_{\{X \geq a\}} \ dP \leq \int I_{\{X \geq a\}} \frac{h(X)}{h(a)} \ dP \leq \frac{\textrm{E}\left[h(X)\right]}{h(a)}$

Varianten

• Setzt man h(x) = x und betrachtet die reelle Zufallsvariable | X | , so erhält man den bekannten Spezialfall der Markow-Ungleichung

$P\left[|X| \geq a\right] \leq \frac{\textrm{E}\left[|X|\right]}{a}.$

• Betrachtet man $a = c \cdot \textrm{E}[|X|]$ für ein c > 0, so folgt der bekannte Spezialfall der Markow-Ungleichung, welcher die Wahrscheinlichkeit für das c-fache Übertreffen des Erwartungswertes begrenzt:

$P\left[|X| \geq c \cdot \textrm{E}[|X|] \right] \leq \frac{\textrm{E}\left[|X|\right]}{c \cdot \textrm{E}\left[|X|\right]} = \frac{1}{c}.$

• Ist h(x) = x² und wendet man die Markow-Ungleichung auf eine Zufallsvariable Y = X − E[X] an, so erhält man eine Version der Tschebyschow-Ungleichung.

• Für beschränkte Zufallsvariablen existiert die folgende Markow-artige Schranke für die Wahrscheinlichkeit, dass eine Zufallsvariable ihren Erwartungswert um den Faktor (1 − c) unterbietet. D.h., seien 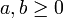$a,b \geq 0$ und sei X eine Zufallsvariable mit 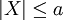$|X| \leq a$ und $\textrm{E}\left[|X|\right] \geq \frac{a}{b}$. Dann gilt für alle c > 0:

$P\left[ |X| \leq (1-c)\textrm{E}\left[|X|\right] \right] \leq 1-\frac{c}{b}.$

Der Beweis dieser Aussage ist ähnlich dem Beweis der Markow-Ungleichung.^[1]

• Wählt man h(x) = e^tx, erhält man für geeignetes t eine sehr gute Abschätzung. Mann kann zeigen, dass diese Abschätzung unter gewissen Voraussetzungen sogar optimal ist.

Beispiele

Betrachte die folgende Frage: Wie wahrscheinlich ist es, bei einem Würfelwurf wenigstens eine 4 zu würfeln? Es sei X das Ergebnis des Würfelwurfes mit E[X] = 3,5. Dann folgt mit h(x) = x als identische Abbildung und mit a = 4 durch die Markow-Ungleichung:

$P \left[ X \geq 4 \right] \leq \frac{\textrm{E}\left[X\right]}{4} = \frac{3{,}5}{4} = \frac{7}{8}$.

Einzelnachweise

1. ↑ Piotr Indyk, Sublinear Time Algorithms for Metric Space Problems, Proceedings of the 31st Symposium on Theory of Computing (STOC'99), 428--434, 1999.