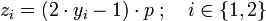Marsaglias polare Methode

Die Polar-Methode von George Marsaglia ist ein Verfahren zur Erzeugung normalverteilter Zufallszahlen (Zufallszahlengenerator).

Mit dieser Methode werden aus zwei gegebenen, im Intervall [0,1] gleichverteilten und voneinander unabhängigen Zufallszahlen y₁ und y₂ zwei standardnormalverteilte, voneinander unabhängige Zufallszahlen z₁ und z₂ erzeugt.

Zunächst wird berechnet

$q = (2 \cdot y_1 - 1)^2 + (2 \cdot y_2 - 1)^2$.

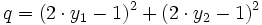Ist q > 1, müssen zwei neue Zahlen y₁ und y₂ erzeugt werden. Wenn $q \le 1$ ist, berechnet man

$p = \sqrt{\frac{-2 \ln q}{q}}$.

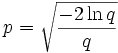Die beiden standardnormalverteilten Zufallszahlen z₁ und z₂ ergeben sich dann als

$z_i=(2 \cdot y_i - 1) \cdot p \; ; \quad i\in \{1,2\}$

Geschichte

Diese Methode geht zurück auf den Box-Muller Algorithmus zur Erzeugung normalverteilter Zufallsgrößen. Ausgangspunkt ist ein gleichverteilter Punkt in der Ebene. Beim Box-Muller Algorithmus werden die euklidischen Koordinaten verwertet. Bei der Polar-Methode werden diese euklidischen Koordinaten in Polarkoordinaten umgewandelt. Dadurch spart man sich hier die Auswertung von trigonometrischen Funktionen.

Alternativen

Alternativen sind im Artikel Normalverteilung beschrieben.