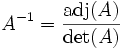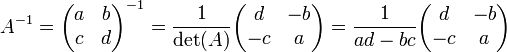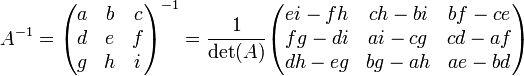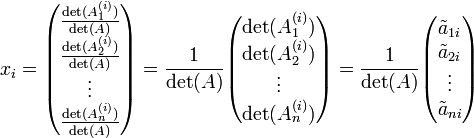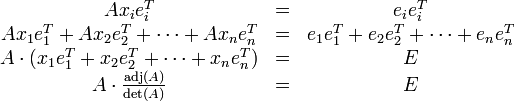- Matrizeninversion
-
Die reguläre, invertierbare oder nichtsinguläre Matrix ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit eine quadratische Matrix A, zu der eine weitere Matrix A − 1 existiert, so dass
gilt. Dabei ist E die Einheitsmatrix, und A − 1 wird als inverse Matrix zu A bezeichnet oder einfach kurz als Inverse.
Invertierbare Matrizen zeichnen sich dadurch aus, dass die durch sie beschriebene lineare Abbildung bijektiv ist. Dies führt dazu, dass ein lineares Gleichungssystem mit einer invertierbaren Koeffizientenmatrix eindeutig lösbar ist.
Nicht zu jeder quadratischen Matrix existiert eine Inverse. Die Menge aller invertierbaren
 –Matrizen über einem Grundkörper (oder Grundring) K bildet eine Gruppe bezüglich der Matrixmultiplikation, die allgemeine lineare Gruppe GLn(K).
–Matrizen über einem Grundkörper (oder Grundring) K bildet eine Gruppe bezüglich der Matrixmultiplikation, die allgemeine lineare Gruppe GLn(K).Das Gegenteil von regulärer Matrix ist eine singuläre Matrix. Matrizen sind singulär, falls sie keine Inverse besitzen (ihre Determinante verschwindet dann). Die Pseudoinverse stellt eine Verallgemeinerung der inversen Matrix auf singuläre und nichtquadratische Matrizen dar.
Inhaltsverzeichnis
Berechnung der inversen Matrix
Zur Berechnung der Inversen stehen zwei Möglichkeiten zur Verfügung: der Gauß-Jordan-Algorithmus und die Adjunkte. Insbesondere mittels der Adjunkte lassen sich prinzipiell Formeln für Matrizen mit festgelegtem Rang herleiten. Diese sind jedoch zu umfangreich, um effizient eingesetzt werden zu können, so dass nur für 2x2- und 3x3-Matrizen gelegentlich die unten aufgeführten Formeln verwendet werden.
Um die numerische Qualität von Algorithmen zur Invertierung von Matrizen zu testen, verwendet man die Hilbert-Matrix, da diese vergleichsweise schlecht konditioniert ist.
Gauß-Jordan-Algorithmus
Die Inverse einer Matrix kann aus der Formel
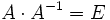 berechnet werden. Dazu bildet man die Blockmatrix (A | E) und wendet auf diese den Gauß-Jordan-Algorithmus an. Nach Durchführung des Algorithmus hat man eine Blockmatrix (E | A − 1), aus der man A − 1 direkt ablesen kann.
berechnet werden. Dazu bildet man die Blockmatrix (A | E) und wendet auf diese den Gauß-Jordan-Algorithmus an. Nach Durchführung des Algorithmus hat man eine Blockmatrix (E | A − 1), aus der man A − 1 direkt ablesen kann.Beispiel:
Gesucht ist die Inverse zur Matrix
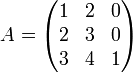 .
.
Die Blockmatrix (A | E) lautet
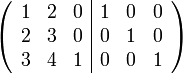 .
.
Die Anwendung des Gauß-Jordan-Algorithmus führt zur Matrix
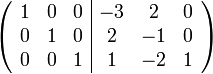 .
.
Daraus lässt sich die inverse Matrix direkt ablesen:
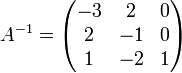 .
.
Adjunkte
Mittels der Adjunkte und der Determinante einer Matrix berechnet sich deren Inverse nach folgender Formel:
Daraus leiten sich für
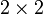 - und
- und 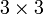 -Matrizen die folgenden Formeln ab:
-Matrizen die folgenden Formeln ab:Formel für 2x2-Matrizen
Formel für 3x3-Matrizen
Herleitung der Formel
Die Idee, die Inverse einer Matrix mittels der Adjunkten zu berechnen, leitet sich direkt aus der cramerschen Regel ab. Nach dieser lässt sich das Gleichungssystem
- Axi = ei
mit dem i-ten Einheitsvektor auf der rechten Seite durch
lösen. Dabei entsteht die Matrix
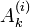 aus A, indem man die k-te Spalte durch den i-ten Einheitsvektor ersetzt. Deren Determinante ist auf Grund der einfachen Gestalt des Einheitsvektors mit dem Cofaktor
aus A, indem man die k-te Spalte durch den i-ten Einheitsvektor ersetzt. Deren Determinante ist auf Grund der einfachen Gestalt des Einheitsvektors mit dem Cofaktor 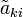 identisch. Es zeigt sich, dass die xi den Spalten der zu A inversen Matrix entsprechen. Dazu multipliziert man beide Seiten des eingangs gezeigten Gleichungssystems von rechts mit dem transponierten i-ten Einheitsvektor
identisch. Es zeigt sich, dass die xi den Spalten der zu A inversen Matrix entsprechen. Dazu multipliziert man beide Seiten des eingangs gezeigten Gleichungssystems von rechts mit dem transponierten i-ten Einheitsvektor 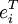 und bildet die Summe über alle i.
und bildet die Summe über alle i.Besondere Klassen von Matrizen
Es gibt einige Klassen von Matrizen, die auf Grund ihrer Struktur besonders einfach zu invertieren sind. Dazu zählen die Diagonalmatrizen und die Dreiecksmatrizen.
Definition
Invertierbare Matrizen über einem Körper
Es sei K ein Körper, also z. B.
 oder
oder  , und A sei eine
, und A sei eine  -Matrix mit Einträgen aus K.
-Matrix mit Einträgen aus K.Dann ist A genau dann invertierbar, wenn eine der folgenden äquivalenten Bedingungen erfüllt ist:
- Es gibt eine inverse Matrix A − 1, d. h. AA − 1 = A − 1A = In mit der Einheitsmatrix In.
- Die Determinante von A ist nicht null.
- 0 ist kein Eigenwert von A.
- Für alle
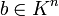 existiert genau eine Lösung
existiert genau eine Lösung 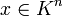 des linearen Gleichungssystems Ax = b.
des linearen Gleichungssystems Ax = b. - Für alle
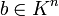 existiert mindestens eine Lösung
existiert mindestens eine Lösung 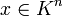 des linearen Gleichungssystems Ax = b.
des linearen Gleichungssystems Ax = b. - Für alle
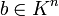 existiert höchstens eine Lösung
existiert höchstens eine Lösung 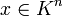 des linearen Gleichungssystems Ax = b.
des linearen Gleichungssystems Ax = b. - Die Zeilenvektoren bilden eine Basis von Kn.
- Die Zeilenvektoren sind linear unabhängig.
- Die Zeilenvektoren erzeugen Kn.
- Die Spaltenvektoren bilden eine Basis von Kn.
- Die Spaltenvektoren sind linear unabhängig.
- Die Spaltenvektoren erzeugen Kn.
- Die durch A beschriebene lineare Abbildung
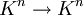 ,
, 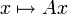 , ist bijektiv.
, ist bijektiv. - Die durch A beschriebene lineare Abbildung
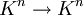 ,
, 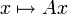 , ist injektiv.
, ist injektiv. - Die durch A beschriebene lineare Abbildung
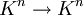 ,
, 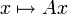 , ist surjektiv.
, ist surjektiv. - Die transponierte Matrix AT ist invertierbar.
Invertierbare Matrizen über einem Ring
Es sei R ein kommutativer Ring mit Einselement, und A sei eine
 -Matrix mit Einträgen aus R. In dieser allgemeineren Situation sind nicht mehr alle der obigen Kriterien für die Invertierbarkeit gültig.
-Matrix mit Einträgen aus R. In dieser allgemeineren Situation sind nicht mehr alle der obigen Kriterien für die Invertierbarkeit gültig.Die Matrix A ist genau dann invertierbar, wenn eine der folgenden äquivalenten Bedingungen erfüllt ist:
- Es gibt eine inverse Matrix A − 1, d. h. AA − 1 = A − 1A = In mit der Einheitsmatrix In.
- Die Determinante von A ist eine Einheit in R.
- Für alle
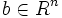 existiert genau eine Lösung
existiert genau eine Lösung 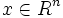 des linearen Gleichungssystems Ax = b.
des linearen Gleichungssystems Ax = b. - Die Zeilenvektoren bilden eine Basis von Rn.
- Die Spaltenvektoren bilden eine Basis von Rn.
- Die durch A beschriebene R-lineare Abbildung
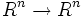 ,
, 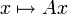 , ist bijektiv.
, ist bijektiv. - Die transponierte Matrix AT ist invertierbar.
- Für alle
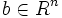 existiert mindestens eine Lösung
existiert mindestens eine Lösung 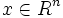 des linearen Gleichungssystems Ax = b.
des linearen Gleichungssystems Ax = b. - Die Zeilenvektoren erzeugen Rn.
- Die Spaltenvektoren erzeugen Rn.
- Die durch A beschriebene R-lineare Abbildung
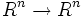 ,
, 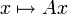 , ist surjektiv.
, ist surjektiv.
Eigenschaften
Ist λ ein Eigenwert der regulären Matrix A mit Eigenvektor
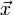 , so ist
, so ist  Eigenwert der inversen Matrix A − 1 ebenfalls zum Eigenvektor
Eigenwert der inversen Matrix A − 1 ebenfalls zum Eigenvektor 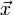 .
.Rechenregeln
Das Produkt zweier invertierbarer Matrizen ist wieder invertierbar. Es gilt
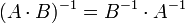 .
.
Die Inverse der transponierten Matrix entspricht der Transponierten der inversen Matrix:
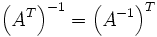 .
.
Die Inverse einer Matrix A ist ebenfalls invertierbar. Die Inverse der Inversen ist gerade wieder die Matrix selbst:
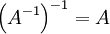 .
.
Die Inverse einer Matrix A multipliziert mit einem Skalar
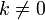 ist
ist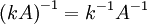 .
.
Weblinks
Wikimedia Foundation.