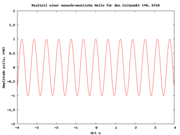
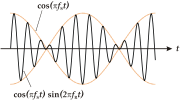
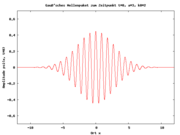
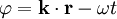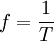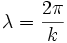- Mechanische Welle
-
Eine Welle ist ein räumlich und zeitlich veränderliches Feld, das Energie durch den Raum transportiert. Ein im Raum eventuell vorhandenes Medium wird durch eine Welle nicht dauerhaft verschoben. Mechanische Wellen sind Schwingungen, die sich durch eine Kette elastisch gekoppelter Massen - sog. Oszillatoren - in einem Medium ausbreiten. Elektromagnetische Wellen benötigen kein Medium und sind auch im Vakuum ausbreitungsfähig. Bekannt sind vor allem Schallwellen, Wasserwellen und elektromagnetische Wellen, beispielsweise in Form von Radiowellen oder Licht.
Inhaltsverzeichnis
Allgemeines
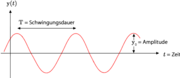
Wellen können als periodische Wellen (klingender Ton) oder als Stoßwellen (Knall) auftreten. Die wichtigsten Eigenschaften einer Welle sind ihre Amplitude (z. B. Lautstärke), ihre Ausbreitungsgeschwindigkeit (Schallgeschwindigkeit) und Frequenz bzw. Wellenlänge (Tonhöhe bei Schall, Farbe bei Licht, usw.).
Bei einigen Wellentypen wird ein Medium (Gase, Festkörper oder Flüssigkeiten) zur Wellenerzeugung benötigt: z. B. Schall und Wasserwellen. Elektromagnetische Wellen benötigen kein Medium, hier breiten sich die Schwingungszustände über die Änderung von elektrischen und magnetischen Feldern aus.
Wichtige Effekte, die bei allen Wellenarten auftreten können, sind Brechung, Beugung und Interferenz.
Pendelwellen
Einzelpendel
Ein Pendel führt, wenn man es anstößt, Schwingungen aus. Breiten sich die Schwingungen in einem Medium (z. B. Luft, Wasser) aus, so entsteht eine Welle. Diesen Vorgang kann man an folgendem Beispiel gut veranschaulichen:
Als Quelle dient ein schwingendes Pendel, an dessen unterem Ende ein Bleistift befestigt ist. Das Medium, in dem sich die Welle ausbreitet, ist ein Papierstreifen, der mit gleichmäßiger Geschwindigkeit unter dem Pendel durchgezogen wird. Der am Pendel befestigte Bleistift beschreibt nun auf dem Papierstreifen eine (annähernd) sinusförmige Welle. Bei diesem Beispiel ist die Wellenlänge (Lambda) abhängig von der Geschwindigkeit, mit der der Papierstreifen bewegt wird. Die Amplitude der Welle wird durch den maximalen Pendelausschlag bestimmt.
Gekoppelte Pendel
Ein einzelnes Pendel führt, wenn man es anstößt, Schwingungen aus. Verbindet man mehrere nebeneinander befindliche Pendel durch elastische Spiralfedern, so entsteht eine Reihe gekoppelter Pendel. Stößt man nun ein Pendel an, so werden durch die elastischen Federn auch die benachbarten Pendel in Schwingung versetzt, während das anfangs angestoßene Pendel dadurch wieder gebremst wird. So kommt das erste Pendel recht bald wieder zur Ruhe während sich nun weiter entfernte Pendel in Bewegung befinden.
In diesem Modell sind die Pendel das Medium, in dem sich die Welle ausbreitet. Ein einzelnes Pendel ist ein Teilchen dieses Modell-Mediums. Die elastischen Federn stellen die Kopplung zwischen den Teilchen dar. Die Fortpflanzung oder Ausbreitung der Pendelbewegung ist die eigentliche Welle.
Der Informationstransport besteht hierbei in der Tatsache, dass ein Beobachter eines entfernten Pendels einen Ausschlag sieht, nachdem das erste Pendel angestoßen wurde (wenn auch mit einem messbaren Zeitversatz).
Der Energietransport ist zu verstehen, wenn man neben einem entfernten Pendel eine Kugel ablegt. Nun kann man durch Anstoßen des ersten Pendels die Kugel am entfernten Pendel (wiederum nach kurzer Zeit) in Bewegung versetzen.Wellentypen
Wellen entspringen zumeist dem von Lagrange untersuchten Wechselspiel zwischen potentieller und kinetischer Energie. Zwei unterschiedliche Größen, meistens Energieformen, werden dabei ineinander umgewandelt, z. B.: Druck und Bewegung (Kinetische Energie) bei der Schallwelle, Lageenergie und Bewegung bei der Wasserwelle, Magnetfeld und elektrisches Feld bei der Radiowelle. Sie können nach folgenden Kriterien klassifiziert werden.
- Mechanische Wellen: Wellen, die an ein Medium gebunden sind
- Longitudinalwellen/Längswellen: Die Schwingung/Störung des Mediums erfolgt parallel zur Ausbreitungsrichtung.
Schall als Druckwelle, in Luft, in Festkörpern (Lärm dringt auch durch Fensterscheiben) oder in Flüssigkeiten, Walgesang. - Transversalwellen/Querwellen: Die Schwingung/Störung des Mediums erfolgt senkrecht zur Ausbreitungsrichtung.
Wasserwellen als Oberflächenwellen. Sie breiten sich waagerecht aus, die Schwingung selbst erfolgt jedoch in der Senkrechten, Wasser hebt und senkt sich (vereinfachtes Modell).
- Longitudinalwellen/Längswellen: Die Schwingung/Störung des Mediums erfolgt parallel zur Ausbreitungsrichtung.
- Wellen im Vakuum
- Elektromagnetische Wellen (Strahlung)
- Materiewellen: Nach der Theorie von Louis de Broglie kann auch einem sich bewegenden Teilchen eine Wellenlänge zugeordnet werden.
- Wahrscheinlichkeitswellen: Die Quantentheorie beschreibt physikalische Vorgänge mit Hilfe sog. Wahrscheinlichkeitswellen. Diese Wellen sind weder direkt beobachtbar noch messbar, sondern dienen als abstraktes, mathematisches Vehikel zur Beschreibung physikalischer Sachverhalte.
- Gravitationswellen: Obwohl noch nicht nachgewiesen, nimmt man an, dass auch die Gravitationskraft unter bestimmten Umständen eine Quelle für Wellen sein kann. Die einfachste Modellvorstellung hierfür wäre ein Doppelsternsystem mit hoher Rotationsfrequenz, bestehend aus sehr massiven Sternen. In diesem Fall ist die Entstehung der Welle analog zur Entstehung einer Radiowelle in einer Antenne (elektromagnetischer Dipol) zu verstehen.
Mathematische Beschreibung
Wellenfunktion
Von Wellen spricht man bei Phänomenen, die der Wellengleichung (oder einer ihrer Ableitungen wie der Schrödingergleichung) genügen. Deren Lösungen sind Funktionen von der Gestalt
Dabei gibt
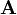 die Auslenkung am Ort
die Auslenkung am Ort 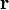 zur Zeit
zur Zeit 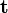 an. Funktionen dieses Typs entsprechen der Vorstellung, dass Wellen räumlich ausgedehnte Schwingungen sind. Eine allgemeine Funktion für jede Art von Welle anzugeben, ist dabei nicht ohne weiteres möglich. Häufig werden daher sehr einfache Lösungen der Wellengleichung herangezogen und die reale Welle als eine Überlagerung von vielen dieser Lösungen angesehen. Die gebräuchlichsten Elementarlösungen sind die Ebene Welle und die Kugelwelle.
an. Funktionen dieses Typs entsprechen der Vorstellung, dass Wellen räumlich ausgedehnte Schwingungen sind. Eine allgemeine Funktion für jede Art von Welle anzugeben, ist dabei nicht ohne weiteres möglich. Häufig werden daher sehr einfache Lösungen der Wellengleichung herangezogen und die reale Welle als eine Überlagerung von vielen dieser Lösungen angesehen. Die gebräuchlichsten Elementarlösungen sind die Ebene Welle und die Kugelwelle.- Ebene Welle
- Diese zeichnen sich durch ihre ebenen Wellenfronten aus. Beispielsweise erzeugt ein Wellenbad Wasserwellen mit ebener Front. Die mathematische Formulierung für eine sinusförmige Welle im dreidimensionalen Raum ist in komplexer Schreibweise:
- Eine Erläuterung der verwendeten Größen folgt weiter unten. Anschaulicher wird diese Formel für den Fall einer sich in x-Richtung ausbreitenden Welle:
- Kugelwelle
- Wellen dieser Art haben kugelförmige Wellenfronten. Ein Stein, der ins Wasser fällt, erzeugt solche Wellen. Die mathematische Formel für Kugelwellen lautet:
![\mathbf A(\mathbf r,t)=\mathrm{Re}\left(\frac{\mathbf A_0}{r} \exp\left[\mathrm i(kr-\omega t)\right]\right)](/pictures/dewiki/99/c88d3c5fe855761f7009c5368a32dd30.png) ,
,
- mit
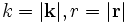
Physikalische Interpretation
Bezeichnung Symbol Beziehungen Amplitude 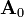
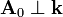
Transversalwelle 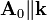
Longitudinalwelle Wellenvektor 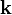
Ausbreitungsrichtung Wellenzahl 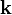
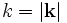
Wellenlänge 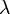
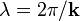
(Kreis-)frequenz 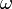
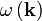 Dispersionsrelation
DispersionsrelationFrequenz f 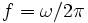
Phasengeschwindigkeit c 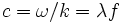
Gruppengeschwindigkeit vG 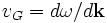
Phase 
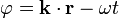
Generell wird eine Welle mit zwei Größen beschrieben: Der Amplitude und der Phase.
Amplitude
Die Amplitude ist die maximale mögliche Auslenkung der Welle. Sie ist bei Wellen – im Gegensatz zu Schwingungen – eine vektorielle Größe, da neben der Stärke der Auslenkung auch deren Richtung entscheidend ist. Ist die Ausbreitungsrichtung parallel zur Amplitude, so spricht man von einer Longitudinalwelle, ist sie senkrecht, von einer Transversalwelle. In beiden Fällen ist die Intensität der Welle proportional zum Amplitudenquadrat.
Phase
Die Phase einer Welle gibt an, in welchem Abschnitt innerhalb einer Periode sich die Welle zu einem Referenzzeitpunkt und -ort befindet. Sie legt also fest, wie groß die Auslenkung ist. Im Beispiel einer ebenen Welle ist
die Phase zum Zeitpunkt t am Ort
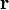 . Wie sich hieran erkennen lässt, hängt die Phase von zwei Parametern ab – dem Wellenvektor
. Wie sich hieran erkennen lässt, hängt die Phase von zwei Parametern ab – dem Wellenvektor 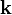 und der Kreisfrequenz ω (omega).
und der Kreisfrequenz ω (omega).- (Kreis-)Frequenz
- Die Frequenz ist ein Maß für Anzahl der Schwingungen pro Zeiteinheit. Hat die Welle eine Periodendauer T, so lautet die Frequenz f:
- Häufig wird jedoch auch die Kreisfrequenz ω = 2πf kurz als Frequenz bezeichnet.
- Wellenvektor
- Im Wellenvektor stecken zweierlei Informationen. Die Richtung des Vektors gibt die Ausbreitungsrichtung der Welle an (z. B. radiale Richtung bei Kugelwellen). Den Betrag k des Vektors nennt man auch Wellenzahl, diese hat einen einfachen Zusammenhang mit der Wellenlänge λ (lambda):
- Die Wellenlänge ist die räumliche Distanz zwischen zwei Punkten, bei denen sich die Welle wiederholt. Die Wellenzahl kann man folglich als eine Art „räumliche Frequenz“ ansehen.
- Frequenz und Wellenvektor einer Welle sind abhängig voneinander. Den Zusammenhang
- bezeichnet man als Dispersionsrelation. Diese hängt von der Wellenart wie auch dem Medium, in dem sich die Welle ausbreitet, ab. Aus der Dispersionsrelation leitet sich die Ausbreitungsgeschwindigkeit der Welle ab. Man unterscheidet hierbei zwischen Phasen- und Gruppengeschwindigkeit.
Überlagerung von Wellen
In der Natur vorkommende Wellen sind in den seltensten Fällen reine monochromatische Wellen, sondern eine Überlagerung aus vielen Wellen unterschiedlicher Wellenlängen. Die Anteile der Wellenlängen werden als Spektrum bezeichnet. Beispiele:
- Sonnenlicht ist eine Überlagerung aus elektromagnetischen Wellen. Das Spektrum umfasst einen Wellenlängenbereich von Infrarot über sichtbares Licht bis Ultraviolett. Derartige Spektren bezeichnet man auch als kontinuierlich.
- Ein Musikton eines Instrumentes setzt sich zusammen aus einem Grundton und mehreren Oberschwingungen. Die unterschiedlichen Anteile an Oberschwingungen sind der Grund warum eine Posaune anders klingt als eine Flöte. Ein solches Spektrum heißt diskret, da es sich nur aus einzelnen Wellenlängen zusammensetzt.
Mathematisch gesehen ist die Wellenfunktion einer Überlagerung zweier Wellen lediglich die Addition von deren Wellenfunktionen. Man bezeichnet dieses als Superpositionsprinzip. Dabei kann es zu folgenden Effekten kommen:
- Interferenz
- Überlagert man Wellen, so kann es zu einer konstruktiven Verstärkung, aber auch zu einer teilweisen oder gar totalen Auslöschung der Welle (wenn beide Wellenlängen und Frequenzen gleich sind und die Wellen genau gegenläufig schwingen) kommen. Dieses Phänomen spielt im Alltag beim Radio eine Rolle – benachbarte Funkzellen strahlen einen Sender auf verschiedenen Frequenzen aus, um Interferenzen im Überlappungsbereich zu vermeiden.
- Stehende Welle
- Bei Überlagerung zweier sich gegenläufig ausbreitender Wellen derselben Frequenz und Amplitude kommt es zur Ausbildung von stehenden Wellen. Diese breiten sich nicht aus, sondern bilden räumlich konstante Schwingungsmuster: An den sogenannten Bewegungsbäuchen schwingen sie mit der verdoppelten Amplitude und der ursprünglichen Frequenz, an den dazwischenliegenden Bewegungsknoten ist die Amplitude zu allen Zeiten Null. Diese Erscheinung ist ein Sonderfall der Interferenz. Sie tritt insbesondere vor einer reflektierenden Wand auf oder auch zwischen zwei passend abgestimmten Wänden, die gemeinsam einen Resonator bilden.
- Schwebung
- Eine Überlagerung zweier Wellen von benachbarter Frequenz führt zu einer Schwebung. Die Amplitude einer solchen Welle nimmt periodisch zu und ab – je näher die Frequenzen beieinander liegen, desto (zeitlich) langsamer geschieht dieser Vorgang. Dieser Effekt wird beispielsweise beim Stimmen von Musikinstrumenten ausgenutzt. Man findet Schwebungen auch bei älteren Telefonaparaten, die einen Wecker mit 2 Glockenschalen haben. Diese Schwebung empfindet der Mensch als angenehm.
- Wellenpaket
- Die Überlagerung von Wellen mit allen Frequenzen aus einem Intervall erzeugt ein Wellenpaket. Hierbei zeigt die Einhüllende der Welle nur einen einzelnen Berg, vor und hinter diesem ist die Amplitude Null. Da die Ausbreitungsgeschwindigkeit einer Welle – insbesondere in Medien – häufig frequenzabhängig ist, laufen solche Wellenpakete mit fortschreitender Zeit auseinander. Bei der Nachrichtenübermittlung mit Lichtpulsen über Glasfaserkabel muss dieses berücksichtigt werden.
Beispiele
- Seegang:
Energieformen: Lageenergie des Wassers und Bewegungsenergie des Wassers. Sonderfall: Bei Überlagerung zweier Wellenzüge ähnlicher Amplitude (das heißt hier: Wellenhöhe) aus unterschiedlicher Richtung spricht man von Kreuzsee, wobei sich zeitweise auch stehende Wellen (siehe oben) ausbilden können. - Schallwellen:
Energieformen: Druck und Schnelle bei Gasen z.B. Luft. Longitudinalwellen. Es gibt aber auch Schallausbreitung in Flüssigkeiten und Festkörpern. Da diese nur wenig kompressibel sind, ist die Schallgeschwindigkeit in Flüssigkeiten und Festkörpern wesentlich größer als in Gasen. - Elektromagnetische Wellen (z. B. Licht):
Energieformen: elektrische und magnetische Feldenergie. Eine vollständige Beschreibung elektromagnetischer Wellen ist nur anhand von Wellen- und Teilcheneigenschaften im Rahmen des Welle-Teilchen-Dualismus möglich. - Autowellen:
Energieformen: Ionenströme an biologischen Membranen und Redoxreaktionen in chemischen Diffusions-Reaktions-Gemischen
Siehe auch
- Doppler-Effekt (Verschiebung der Wellenlänge bei sich relativ zueinander bewegenden Objekten)
- Welle-Teilchen-Dualismus
- Gestörte Ausbreitung: Absorption, Reflexion, Transmission und Dissipation.
- Wellenausbreitung in Hohlleitern
- Beugung
- Interferenz
- Polarisation
- Schwingung
- Druckwelle (sich fortpflanzende Druckschwankungswelle)
- Schall (Schallwellen: sich fortpflanzende Schwingungen in Medien)
- Wasserwelle (eine sich fortpflanzende Schwingung oder Erhebung in Gewässern)
- Tsunami (Durch Seebeben verursachte langwellige Transversalwelle die in Küstengebieten sehr große Schäden anrichten kann)
- Seismische Welle (Welle in der Seismik verschiedene, sich im Erdkörper fortpflanzende Longitudinal- oder Transversalwellen)
- Stoßwelle (explosionsartige Druckwellen)
Weblinks
- Mechanische Wellen: Wellen, die an ein Medium gebunden sind
Wikimedia Foundation.



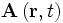
![\mathbf A(\mathbf r,t)=\mathrm{Re}\left(\mathbf A_0\exp\left[\mathrm i\left(\mathbf k\cdot \mathbf r-\omega t\right)\right]\right) \,](/pictures/dewiki/51/3aa7a631b7bfdf74063d50a2499f8372.png)
![\begin{align}\mathbf A(x,t) &= \mathbf{\tilde A}_0 \sin(kx-\omega t + \varphi_0) \\ &= \mathbf{\tilde A}_0 \sin\left[2\pi \left(\frac{x}{\lambda} - f t\right) + \varphi_0\right]\end{align} \,](/pictures/dewiki/56/8809d619a913569c135fa2d350b83c6d.png)