Mehrkörperproblem

Das Dreikörperproblem der Himmelsmechanik besteht darin, eine Lösung für den Bahnverlauf von drei Körpern unter dem Einfluss ihrer gegenseitigen Anziehung (Gravitation) zu finden. Das Dreikörperproblem galt seit den Entdeckungen von Johannes Kepler und Nikolaus Kopernikus als eines der schwierigsten mathematischen Probleme, mit dem sich im Laufe der Jahrhunderte viele bekannte Mathematiker wie Leonhard Euler, Joseph-Louis Lagrange, Thorvald Nicolai Thiele, George William Hill und Henri Poincaré beschäftigten. Den einfacheren Sonderfall, dass einer der drei Körper eine verschwindend kleine Masse hat und seine Wirkung auf die beiden anderen vernachlässigt werden kann, bezeichnet man als eingeschränktes Dreikörperproblem. Das Zweikörperproblem ist durch die Keplerschen Gesetze streng lösbar. Dagegen sind die Integrale im Fall von 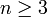$n \geq 3$ Himmelskörpern keine algebraischen Integrale mehr (Satz von Bruns bzw. Poincaré) und sind nicht mehr mit elementaren Funktionen lösbar. Karl Frithiof Sundman konnte Anfang des 20. Jahrhunderts als erster eine analytische Lösung des Dreikörperproblems in Form einer konvergenten Potenzreihe angeben, unter der Annahme, dass der Gesamtdrehimpuls des Systems nicht verschwindet und es deshalb nicht zu einem Dreierstoß kommt.

Die Stabilität eines Dreikörpersystems wird durch das KAM-Theorem [1] beschrieben. Näherungslösungen sind unter anderem möglich, wenn die Masse eines der Himmelskörper klein ist:

• Man löst das Dreikörperproblem dann iterativ, heutzutage mit Computern, oder
• berechnet Bahnstörungen, welche der kleinste (leichteste) Körper durch die größeren (schwereren) erleidet.
• Exakt lösbar ist es jedoch bei Gleichgewicht der Schwerkraft zwischen den großen (schwereren) Körpern, – in den Lagrange-Punkten L1 bis L5. Der innere Punkt L1 wird beispielsweise in der Raumfahrt zur Sonnenforschung verwendet. Das SOHO-Sonnenobservatorium befindet sich dort.
• Für den Sonderfall dreier gleicher Massen gibt es eine weitere Lösung, bei der die Objekte auf einer gemeinsamen Bahn, die die Form eines „$\infty$“ hat, hintereinander her laufen.

Allgemeine Mehrkörperprobleme löst man als Mehrkörpersimulation.

Siehe auch

• Tisserandparameter
• Hill-Sphäre
• Sitnikov-Problem
• Lagrange-Punkt

Weblinks

• Kann man im All parken?, Flash-Video aus der Fernsehsendung alpha-Centauri (JavaScript benötigt)
• Chaos und Komplexitätstheorie (PDF)
• Numerische Berechnungen von Planetenbahnen