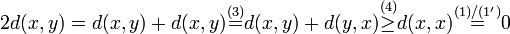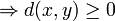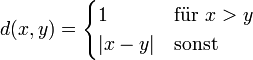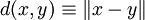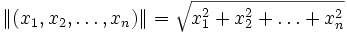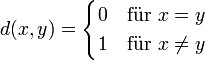- Metriken im Vektorraum
-
metrischer Raum berührt die Spezialgebiete
hat Eigenschaften von
umfasst als Spezialfälle
Beispiele sind
Eine Metrik ist eine mathematische Funktion, die je zwei Elementen eines Raums einen nicht negativen reellen Wert zuordnet, der als Abstand der beiden Elemente voneinander aufgefasst werden kann.
Ein Raum ist eine Menge, deren Elemente in geometrischer Interpretation als Punkte aufgefasst werden. Ein metrischer Raum ist ein Raum, auf dem eine Metrik definiert ist.
Inhaltsverzeichnis
Formale Definition
Sei X eine beliebige Menge. Eine Abbildung
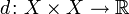 heißt Metrik auf X, wenn für beliebige Elemente x, y und z von X die folgenden axiomatischen Bedingungen erfüllt sind:
heißt Metrik auf X, wenn für beliebige Elemente x, y und z von X die folgenden axiomatischen Bedingungen erfüllt sind: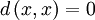 (identische Punkte haben Abstand 0),
(identische Punkte haben Abstand 0),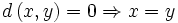 (nichtidentische Punkte haben nicht Abstand 0),
(nichtidentische Punkte haben nicht Abstand 0),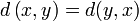 (Symmetrie),
(Symmetrie),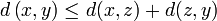 (Dreiecksungleichung).
(Dreiecksungleichung).
(X;d) heißt metrischer Raum, wenn d eine Metrik auf X ist.
In der Praxis bezeichnet man zumeist X allein als den metrischen Raum, wenn aus dem Kontext klar ist, dass in diesem Raum die Metrik d benutzt wird.
Eine Abbildung, welche die Metrik erhält, heißt Isometrie. Figuren, die von einer Isometrie aufeinander abgebildet werden können, heißen kongruent zueinander.
Zur Erläuterung:
- (1) und (2) können durch folgende äquivalente Bedingung ersetzt werden, so dass sich unter Hinzunahme von (3) und (4) eine äquivalente Definition ergibt:
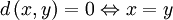 (Definitheit)
(Definitheit)
- Die Nicht-Negativität
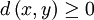 wird oft als zusätzliches Axiom angegeben, folgt aber aus den anderen Bedingungen und ist daher überflüssig, denn:
wird oft als zusätzliches Axiom angegeben, folgt aber aus den anderen Bedingungen und ist daher überflüssig, denn:
- Die Symmetrie (3) besagt, dass es keinen Unterschied zwischen "Hinweg-Abstand" und "Rückweg-Abstand" gibt.
- Die Dreiecksungleichung (4) besagt, dass der Abstand entlang dem direkten Weg, also entlang der kürzesten Verbindung zwischen zwei Punkten gemessen wird. Ein Umweg über einen dritten Punkt kann nicht kürzer als der direkte Weg sein. Wird diese Bedingung dahingehend verschärft, dass der Abstand d(x,y) nicht länger sein darf als der längere der beiden Abstände d(x,z) und d(z,y) (mit beliebigem z!), erhält man den Begriff der Ultrametrik.
Verallgemeinerungen und Spezialisierungen
Durch Abschwächung, Weglassen oder Verschärfung von einer oder mehreren der Bedingungen (1) bis (4) ergeben sich verschiedene Verallgemeinerungen bzw. Spezialisierungen. Die Bezeichnungen für die Verallgemeinerungen sind leider nicht für alle Gebiete der Mathematik, in denen sie verwendet werden, standardisiert. So wird speziell unter einer Semimetrik in der Funktionalanalysis etwas anderes verstanden als in der Topologie (siehe unten).
Pseudometrik
Wird auf Bedingung (2) verzichtet, erhält man den Begriff der Pseudometrik. In der Funktionalanalysis wird hierfür auch die Bezeichnung Halbmetrik oder Semimetrik verwendet. In pseudometrischen Räumen können nichtidentische Punkte den Abstand 0 haben. Eine Pseudometrik ist positiv semidefinit, d. h. Abstände sind stets größer oder gleich 0.
Quasimetrik
Wird auf die Symmetrie d.h. Bedingung (3) verzichtet, erhält man den Begriff der Quasimetrik. Aus einer Quasimetrik d' lässt sich durch
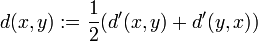 eine Metrik auf X erzeugen.
eine Metrik auf X erzeugen.Nicht-archimedische Metriken
Wird die Dreiecksungleichung d.h. Bedingung (4) abgeschwächt oder verschärft, dann erhält man nicht-archimedische Metriken. Typische Varianten sind
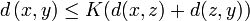 für ein K>1
für ein K>1oder
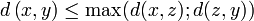 (Ultrametrik).
(Ultrametrik).In der Topologie werden Metriken ohne Dreiecksungleichung manchmal auch als Semimetriken bezeichnet.
Prämetrik
Wird nur Nicht-Negativität und Bedingung (1) gefordert, dann spricht man von einer Prämetrik. Auf
 ist zum Beispiel durch
ist zum Beispiel durcheine solche Prämetrik definiert.
Beispiele: durch Normen erzeugte Metriken
Jede Norm auf einem Vektorraum induziert durch die Festlegung
eine Metrik. Somit ist jeder normierte Vektorraum (und erst recht jeder Innenproduktraum, Banachraum oder Hilbertraum) ein metrischer Raum.
Eine Metrik, die aus einer p-Norm (siehe dazu den Artikel normierter Raum) abgeleitet ist, heißt auch Minkowski-Metrik. Wichtige Spezialfälle sind
- die Manhattan-Metrik zu p = 1;
- die Euklidische Metrik zu p = 2;
- die Maximum-Metrik zu p = ∞.
Weitere Beispiele für Normen (und damit auch für Metriken) finden sich in den Artikeln Matrixnorm, Funktionenraum.
Aus einer p-Norm abgeleitet sind zum Beispiel die Metriken der folgenden wichtigen Räume:
- der eindimensionale Raum der reellen oder komplexen Zahlen mit dem absoluten Betrag als Norm (mit beliebigem p !) und der dadurch gegebenen Metrik
- d(x,y) = | x − y | ;
- der euklidische Raum mit seiner durch den Satz des Pythagoras gegebenen Euklidischen Metrik (zur 2-Norm)
Als eine Fréchet-Metrik wird gelegentlich eine Metrik
- d(x, y) := ρ(x - y)
bezeichnet, die von einer Funktion ρ induziert wird, welche die meisten Eigenschaften einer Norm besitzt, aber nicht homogen ist.
Beispiele: nicht durch Normen erzeugte Metriken
- Auf jeder Menge lässt sich eine triviale Metrik, die sogenannte diskrete Metrik (die sogar eine Ultrametrik ist) definieren durch
- Auf
 wird durch
wird durch 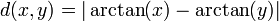 eine Metrik definiert. Bezüglich dieser Metrik ist
eine Metrik definiert. Bezüglich dieser Metrik ist  nicht vollständig. So ist z.B. die Folge
nicht vollständig. So ist z.B. die Folge 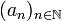 mit
mit 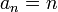 eine Cauchy-Folge, die nicht in
eine Cauchy-Folge, die nicht in  konvergiert. Die von dieser Metrik erzeugten Topologie stimmt mit der auf
konvergiert. Die von dieser Metrik erzeugten Topologie stimmt mit der auf  üblichen Topologie überein. Dies ist ein Beispiel dafür, dass Vollständigkeit kein topologischer Begriff ist.
üblichen Topologie überein. Dies ist ein Beispiel dafür, dass Vollständigkeit kein topologischer Begriff ist.
- Im allgemeinen nicht durch eine Norm induziert ist die riemannsche Metrik, die aus einer differenzierbaren Mannigfaltigkeit eine riemannsche Mannigfaltigkeit macht. Beispiele dafür:
- die natürliche Metrik auf einer Kugeloberfläche, in der der Großkreis die kürzeste Verbindung (Geodäte) zwischen zwei Punkten ist;
- die uneigentliche Metrik im Minkowski-Raum
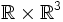 der speziellen Relativitätstheorie, in der zeitähnliche Abstände durch [(Δt)2 - (Δx/c)2 - (Δy/c)2 - (Δz/c)2]1/2 und ortsähnliche Abstände durch [(Δx)2 + (Δy)2 + (Δz)2 - (Δct)2]1/2 gegeben sind;
der speziellen Relativitätstheorie, in der zeitähnliche Abstände durch [(Δt)2 - (Δx/c)2 - (Δy/c)2 - (Δz/c)2]1/2 und ortsähnliche Abstände durch [(Δx)2 + (Δy)2 + (Δz)2 - (Δct)2]1/2 gegeben sind; - die von der Materieverteilung abhängige Verallgemeinerung dieser Metrik in der allgemeinen Relativitätstheorie.
- Die sogenannte französische Eisenbahnmetrik ist ein beliebtes Übungsbeispiel für eine nicht durch eine Norm induzierte Metrik. Sie wird unter Bezugnahme auf einen ausgezeichneten Punkt P („Paris“) wie folgt definiert: Der Abstand zweier verschiedener Punkte, deren Verbindungsgerade durch P verläuft, ist ihr Abstand unter der gewöhnlichen Euklidischen Metrik. Der Abstand zweier verschiedener Punkte, deren Verbindungsgerade nicht durch P verläuft, ist die Summe ihrer Abstände von P.
- Die Hausdorff-Metrik misst den Abstand zwischen Teilmengen, nicht Elementen, eines metrischen Raums; man könnte sie als Metrik zweiten Grades bezeichnen, denn sie greift auf eine Metrik ersten Grades zwischen den Elementen des metrischen Raums zurück.
Einordnung in die Hierarchie mathematischer Strukturen
Metriken geben einem Raum eine globale und eine lokale Struktur. Die globale Struktur kommt in geometrischen Eigenschaften wie der Kongruenz von Figuren zum Ausdruck. Die lokale metrische Struktur, also die Definition kleiner Abstände, ermöglicht unter bestimmten zusätzlichen Voraussetzungen die Einführung von Differentialoperationen.
Der Begriff „topologischer Raum“ verallgemeinert den Begriff „metrischer Raum“: Jeder metrische Raum ist ein topologischer Raum mit der Topologie, die durch die Metrik induziert wird (siehe dazu Umgebung). Jeder metrische Raum ist ein Hausdorff-Raum.
Ein topologischer Raum heißt metrisierbar, wenn er zu einem metrischen Raum homöomorph ist. Damit ist ein topologischer Raum (X,T) metrisierbar, wenn eine Metrik d auf X existiert, welche die Topologie T induziert.
Ein vollständiger metrischer Raum ist ein metrischer Raum, in dem jede Cauchyfolge konvergiert. Siehe dazu den ausführlichen Artikel vollständiger Raum. Ein vollständiger normierter Vektorraum heißt Banachraum. Ein Banachraum, dessen Norm durch ein Skalarprodukt induziert ist, heißt Hilbertraum. Betrachtet man die von einem metrischen Raum erzeugte Topologie, lassen sich diese Begriffe nicht mehr definieren. Eine mögliche Verallgemeinerung, die dies noch erlaubt, bilden die uniformen Räume.
→ Hauptartikel: Hierarchie mathematischer Strukturen
Geschichte
Metrische Räume wurden in der Arbeit Sur quelques points du calcul fonctionnel (1906) von Maurice Fréchet erstmals verwendet. Der Begriff metrischer Raum wurde von Felix Hausdorff geprägt.
Wikimedia Foundation.