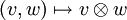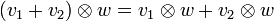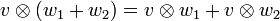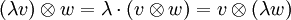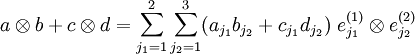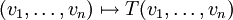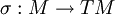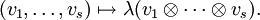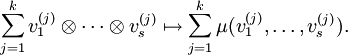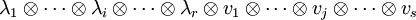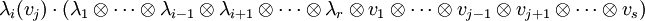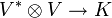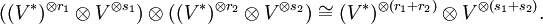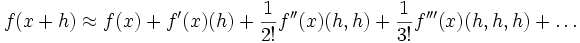- Multilineare Algebra
-
Dieser Artikel erläutert den mathematischen Begriff Tensor, die Muskeln werden unter Musculus tensor fasciae antebrachii, Musculus tensor fasciae latae, Musculus tensor tympani und Musculus tensor veli palatini erläutert. 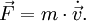
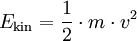
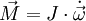
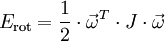
- Ein Tensor nullter Stufe ist eine Zahl, auch Skalar genannt.
- Ein Tensor erster Stufe wird durch einen Spaltenvektor dargestellt. Im n-dimensionalen Raum hat ein solcher Tensor genau n Koeffizienten.
- Ein Tensor zweiter Stufe wird durch eine quadratische Matrix dargestellt, also ein Zahlenschema, in dem jeder der n2 Koeffizienten des Tensors durch zwei Indizes bezeichnet ist (Beispiel: Trägheitstensor).
- Ein Tensor dritter Stufe ließe sich durch eine würfelförmige Anordnung seiner n3 Koeffizienten darstellen, die durch je drei Indizes „adressiert“ werden (Beispiel: der absolut antisymetrische Levi-Civita-Tensor für den 3-dimensionalen Raum).
- Ein Tensor m-ter Stufe hat dementsprechend nm Koeffizienten, die mit Hilfe von m Indizes auseinandergehalten werden. Dabei ist ein Tensor nur dann vollständig bestimmt, wenn zu jeder möglichen Belegung der Indizes der entsprechende Koeffizient angegeben ist. Man kann dies mit einer Datenbank vergleichen, deren Schlüssel aus den m Indizes besteht und in der für jeden zulässigen Schlüssel ein Wert eingetragen ist.
-
-
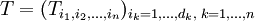 (siehe auch Indexnotation von Tensoren).
(siehe auch Indexnotation von Tensoren).
-
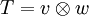 .
.-
-
-
-
-
-
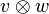 und
und 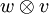 ,
,
-
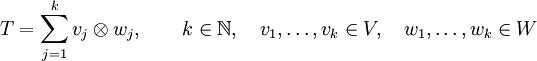
-
-
 .
.
-
-
-
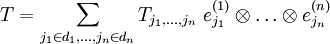 .
.
-
-
-
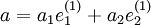 ,
, 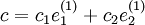 , sowie
, sowie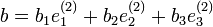 ,
, 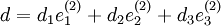 ,
,
-
-
-
-
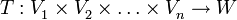 mit der Zuordnung
mit der Zuordnung
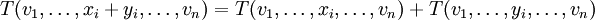
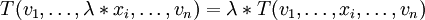 .
.-
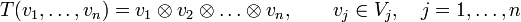 .
.
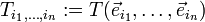
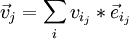

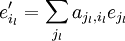
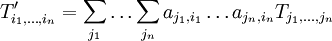
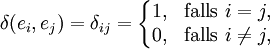
- Siehe auch: Tensordarstellungen der Physik
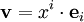
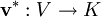
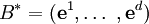
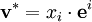
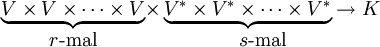
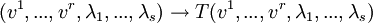
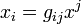
- Tijkj
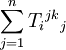 .
.- In der mathematischen Physik versteht man unter einem glatten Vektorfeld σ über einer glatten Mannigfaltigkeit M einen Schnitt im Tangentialbündel (TM,M,πM), d.h. eine
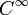 -Abbildung
-Abbildung -
- mit
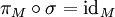 .
.
- Das ist die abstrakte Form von Bewegungsgleichungen erster Ordnung in der Physik. Hier interessiert man sich für die Existenz und Eigenschaften von Lösungen.
- In der angewandten Mathematik bzw. in den Ingenieurswissenschaften liegt das Augenmerk weniger auf Existenz und speziellen Eigenschaften, sondern auf der Berechnung von Lösungen. An Stelle einer n-dimensionalen glatten Mannigfaltigkeit M und des Tangentialbündels TM treten die lokalen Koordinatensysteme.
- Für die Sicht der multilinearen Algebra beschränkt man sich auf die Strukturen in den einzelnen Fasern TxM
-
- Jede weitere bilineare Abbildung
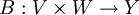 kann auf eindeutiger Weise zu einer linearen Abbildung auf X erweitert werden. Dies heißt exakter, dass es eine einzige lineare Abbildung
kann auf eindeutiger Weise zu einer linearen Abbildung auf X erweitert werden. Dies heißt exakter, dass es eine einzige lineare Abbildung 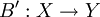 gibt, so dass für beliebige Paare von Vektoren gilt
gibt, so dass für beliebige Paare von Vektoren gilt
- B(v,w) = B'(φ(v,w)).
- Jede weitere bilineare Abbildung
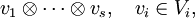
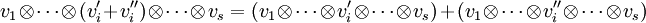
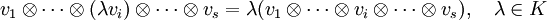
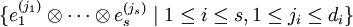
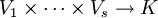
- Ist
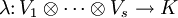 eine Linearform auf
eine Linearform auf 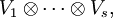 so ist die entsprechende Multilinearform
so ist die entsprechende Multilinearform -
- Ist
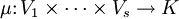 eine s-Multilinearform, so ist die entsprechende Linearform auf
eine s-Multilinearform, so ist die entsprechende Linearform auf 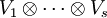 definiert durch
definiert durch -
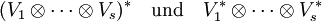

- Einem (r,s)-Tensor kann auf verschiedene Weisen ein (r − 1,s − 1)-Tensor gebildet werden: Für
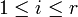 und
und 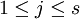 wird einem Tensor
wird einem Tensor -
- der Tensor
- zugeordnet. Dieser Vorgang heißt Tensorverjüngung oder Spurbildung: im Falle von (1,1)-Tensoren entspricht die Abbildung
- unter der Identifizierung
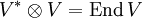 der Spur eines Endomorphismus.
der Spur eines Endomorphismus. - Aus einem (r1,s1)-Tensor und einem (r2,s2)-Tensor kann ein (r1 + r2,s1 + s2)-Tensor gebildet werden:
-
- Ist auf V ein Skalarprodukt gegeben, so können V und V * miteinander identifiziert werden, es gibt also Entsprechungen zwischen (r,s)-Tensoren und (r + k,s − k)-Tensoren.
- Beispiel
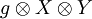
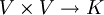 .
.- Die Determinante von
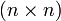 -Matrizen, aufgefasst als alternierende Multilinearform der Spalten, ist ein (n,0)-Tensor.
-Matrizen, aufgefasst als alternierende Multilinearform der Spalten, ist ein (n,0)-Tensor. - Lineare Abbildungen
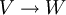 zwischen endlichdimensionalen Vektorräumen können als Elemente von
zwischen endlichdimensionalen Vektorräumen können als Elemente von 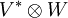 aufgefasst werden.
aufgefasst werden. - Differentialformen vom Grad k, insbesondere das totale Differential einer Funktion im Fall k = 1, sind Schnitte von
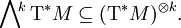
- Riemannsche Metriken sind (2,0)-Tensoren.
- Der riemannsche Krümmungstensor ist ein (3,1)-Tensor, der mithilfe der riemannschen Metrik als (4,0)-Tensor aufgefasst werden kann.
- Ein Vektor
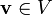 ist mit der Abbildung
ist mit der Abbildung 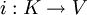 zu identifizieren, welche K auf die Gerade
zu identifizieren, welche K auf die Gerade 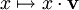 mit der Richtung
mit der Richtung 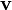 abbildet. Ein Vektor ist also kovariant.
abbildet. Ein Vektor ist also kovariant. - Ein Kovektor
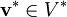 ist als lineares Funktional
ist als lineares Funktional 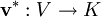 definiert, somit ist er kontravariant in V.
definiert, somit ist er kontravariant in V. 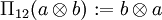 .
.- Ein
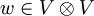 , welches Π12(w): = w erfüllt, heißt symmetrisch. Beispiele sind die Elemente
, welches Π12(w): = w erfüllt, heißt symmetrisch. Beispiele sind die Elemente -
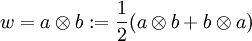 .
.- Die Menge aller symmetrischen Tensoren der Stufe 2 wird mit
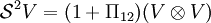 bezeichnet.
bezeichnet.
- Ein
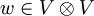 , welches Π12(w): = − w erfüllt, heißt antisymmetrisch oder alternierend. Beispiele sind die Elemente
, welches Π12(w): = − w erfüllt, heißt antisymmetrisch oder alternierend. Beispiele sind die Elemente -
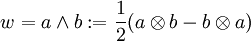 .
.- Die Menge aller antisymmetrischen Tensoren der Stufe 2 wird mit
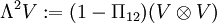 bezeichnet.
bezeichnet.
- in einigen Fällen genügt es, sich Tensoren als eine Verallgemeinerung von Skalar, Vektor, Matrix vorzustellen; in anderen Fällen steht die Invarianz eines Tensors unter Koordinatentransformationen im Vordergrund;
- in einigen Fällen ist es erforderlich, zwischen ko- und kontravarianten Tensoren zu unterscheiden (mehr dazu unten), in anderen Fällen ist diese Unterscheidung irrelevant.
- Algebra: Tensorprodukte sind die algebraische Entsprechung zum kartesischen Produkt geometrischer Objekte.
- Analysis: Die in der Taylorentwicklung einer Funktion in mehreren Veränderlichen
-
- auftretenden multilinearen Ableitungen f(n)(x) kann man als symmetrische, rein kovariante Tensoren aufsteigender Stufe auffassen.
- Differentialgeometrie: Differentialformen und Vektorfelder auf einer Mannigfaltigkeit sind spezielle Tensorfelder, ebenso riemannsche Metriken.
- Physik und Ingenieurwissenschaften: Die physikalische Bedeutung von Tensoren liegt darin begründet, dass Naturgesetze, die durch Tensorgleichungen ausgedrückt werden, in beliebigen Koordinatensystemen die gleiche Gestalt haben („Kovarianz“). Die Tensorsprache erweist sich als besonders zweckmäßig
- in der Elastizitätstheorie, Kontinuumsmechanik, Hydrodynamik;
- in der Elektrodynamik und speziellen Relativitätstheorie;
- sie ist unentbehrlich zum Verständnis der allgemeinen Relativitätstheorie.
- Theodor Bröcker: Lineare Algebra und Analytische Geometrie. Birkhäuser, Basel 2004, ISBN 3-7643-2178-4, Kap. VII: Tensorrechnung.
- R. Abraham, J.E. Marsden, T. Ratiu: Manifolds, Tensor Analysis, and Applications. Second Edition, Springer-Verlag, Berlin, ISBN 3-540-96790-7.
- Theodore Frankel: The Geometry of Physics -- An Introduction. Cambridge University Press 1997, Cambridge, ISBN 0-521-38334-X
- Teichmann Physikalische Anwendungen der Vektor- und Tensorrechnung, BI Hochschultaschenbuch
- Lichnerowicz Einführung in die Tensoranalysis, BI Hochschultaschenbuch 1966
- Über Tensoren, Matrizen und Pseudovektoren (PDF, 132 KB)
- Zur Visualisierung von Vektoren
- Englisches Online Buch über Tensoren und ihre Anwendung von Heinbockel
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!
Als Tensor bezeichnet man eine Verallgemeinerung des Vektorbegriffs in der Differentialgeometrie und der Physik.
In der Physik tauchen Vektoren und Matrizen vor allem als Darstellungen linearer Abbildungen auf (z. B. das Trägheitsmoment). Dies hat zur Folge, dass sich die Darstellungen dieser Größen bei einer Koordinatentransformation in charakteristischer Weise ändern. Mehrdimensionale 'Matrizen' mit entsprechendem Transformationsverhalten werden als Tensoren bezeichnet.
In der Mathematik wird der Begriff allgemeiner über das Tensorprodukt von Moduln und Algebren definiert.
Einleitung
Wort- und Begriffsgeschichte
Das Wort Tensor (lat. tendo: ich spanne) wurde in den 1840er Jahren von Hamilton in die Mathematik eingeführt; er bezeichnete damit den Absolutbetrag seiner Quaternionen, also noch keinen Tensor im modernen Sinn.
Maxwell scheint den Spannungstensor, den er aus der Elastizitätstheorie in die Elektrodynamik übertrug, selbst noch nicht so genannt zu haben.
In seiner modernen Bedeutung, als Verallgemeinerung von Skalar, Vektor, Matrix, wird das Wort Tensor erstmals von Woldemar Voigt in seinem Buch Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung (Leipzig, 1898) eingeführt.
Unter dem Titel absolute Differentialgeometrie entwickelten Gregorio Ricci-Curbastro und dessen Schüler Tullio Levi-Civita um 1890 die Tensorrechnung auf riemannschen Mannigfaltigkeiten; einem größeren Fachpublikum machten sie ihre Ergebnisse 1900 mit dem Buch Calcolo differenziale assoluto zugänglich, das bald in andere Sprachen übersetzt wurde, und aus dem sich Einstein unter großer Mühe die mathematischen Grundlagen aneignete, die er zur Formulierung der allgemeinen Relativitätstheorie benötigte. Einstein selbst prägte 1916 den Begriff Tensoranalysis und trug mit seiner Theorie maßgeblich dazu bei, den Tensorkalkül bekannt zu machen; er führte überdies die einsteinsche Summenkonvention ein, nach der über doppelt auftretende Indizes stillschweigend summiert wird.
Tensoren in der Physik
Einführung
Viele physikalische Gesetze sind Proportionalitäten. Beispielsweise bewirkt eine an einem Körper angreifende Kraft eine Geschwindigkeitsänderung, die der Größe der Kraft proportional ist:
Diese Gleichung besagt zudem, dass die Richtung der Kraft auch die Richtung der Beschleunigung angibt. Derselbe Proportionalitätsfaktor, die Masse m, taucht auch in der Formel für die Bewegungsenergie
auf.
Es gibt jedoch Zusammenhänge, die sich nicht in dieser Weise beschreiben lassen, weil die zugehörigen Proportionalitätsfaktoren von der Richtung der beteiligten vektoriellen Größen abhängen. Ein Beispiel liefern Drehbewegungen: Greift an einem rotierenden Körper ein Drehmoment an, so bewirkt es eine Änderung der Winkelgeschwindigkeit, und eine Verdoppelung des Drehmomentes verdoppelt auch diesen Effekt. Es gilt also
mit einem Proportionalitätsfaktor J, der je nach Richtung von 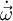 unterschiedlich sein kann, so dass die Richtungen von
unterschiedlich sein kann, so dass die Richtungen von 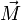 und
und 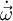 nicht übereinstimmen müssen. Die Rotationsenergie lässt sich ebenfalls mit einem richtungsabhängigen Faktor J als
nicht übereinstimmen müssen. Die Rotationsenergie lässt sich ebenfalls mit einem richtungsabhängigen Faktor J als
darstellen.
Diese Richtungsabhängigkeit bedeutet, dass das Trägheitsmoment J eine tensorielle Größe ist, genauer ein Tensor zweiter Stufe, der Trägheitstensor. „Stufe zwei“ besagt dabei, dass zwei Vektoren beteiligt sind, in der ersten Formel wird über den Trägheitstensor J der Vektor 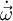 auf den Vektor
auf den Vektor 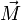 abgebildet (lineare Abbildung), in der zweiten Energieformel tritt der Tensor als Bestandteil einer Bilinearform auf, die dem Drehimpuls-Vektor
abgebildet (lineare Abbildung), in der zweiten Energieformel tritt der Tensor als Bestandteil einer Bilinearform auf, die dem Drehimpuls-Vektor 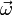 einen Skalar zuordnet (die Energie). Tensoren der zweiten Stufe können also grob gesagt aus Vektoren wieder Vektoren machen oder aus Paaren von Vektoren Zahlen. Mathematisch entspricht das einer linearen Abbildung bzw. einer Bilinearform, die sich beide durch eine
einen Skalar zuordnet (die Energie). Tensoren der zweiten Stufe können also grob gesagt aus Vektoren wieder Vektoren machen oder aus Paaren von Vektoren Zahlen. Mathematisch entspricht das einer linearen Abbildung bzw. einer Bilinearform, die sich beide durch eine 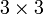 -Matrix beschreiben lassen. Rechnerisch ist ein Tensor zweiter Stufe also nichts anderes als eine (quadratische) Matrix. Durch Hauptachsentransformation der Matrix lassen sich die Haupt-Trägheitsmomente bestimmen (siehe Trägheitsellipsoid).
-Matrix beschreiben lassen. Rechnerisch ist ein Tensor zweiter Stufe also nichts anderes als eine (quadratische) Matrix. Durch Hauptachsentransformation der Matrix lassen sich die Haupt-Trägheitsmomente bestimmen (siehe Trägheitsellipsoid).
Tensoren als Verallgemeinerung von Skalar, Vektor und Matrix
Für manche Anwendungen, zum Beispiel in der Elastizitätstheorie und fast überall in den Ingenieurwissenschaften, ist es häufig ausreichend, sich Tensoren als eine Fortsetzung der Reihe Skalar, Vektor, Matrix vorzustellen. Dabei unterscheidet man Tensoren verschiedener Stufen (auch Rang genannt):
Ein Tensor n-ter Stufe ist also allgemein eine n-fach indizierte Größe
Oft wird der Tensor nur mit dem in Klammern stehenden indexbehafteten Symbol 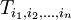 bezeichnet.
bezeichnet.
Jeder Index, beispielsweise i1, durchläuft einen vorbestimmten Wertebereich natürlicher Zahlen, beispielsweise i1 = 1,2,3. Zu jeder möglichen Indexkombination enthält der Tensor eine reelle oder komplexe Zahl. Die indizierte Größe kann sowohl ein Skalar (n = 0), einen Vektor (n = 1) oder eine Matrix (n = 2) darstellen. Insofern handelt es sich um eine Verallgemeinerung der Größen Skalar, Vektor und Matrix.
Es muss aber betont werden, dass für Tensoren ein bestimmtes Transformationsverhalten unter Koordinatentransformationen gefordert wird. Das sind zum Beispiel Drehungen im gewöhnlichen euklidischen Raum oder Lorentz-Transformationen in der Relativitätstheorie. In beiden Fällen lassen die Transformationen eine quadratische Form invariant (die eine Metrik in den zugrundeliegenden Vektorräumen definiert). Man spricht dann auch davon, dass die entsprechenden Tensoren „Darstellungen“ der entsprechenden Gruppen von Transformationen bilden.
Tensor als Tensorprodukt von Vektoren
Als Tensorprodukt wird eine Verknüpfung 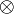 zwischen zwei Vektoren v und w der Vektorräume V und W über demselben Körper K definiert. Diese Verknüpfung wird in der üblichen Form zweistelliger Rechenoperationen notiert,
zwischen zwei Vektoren v und w der Vektorräume V und W über demselben Körper K definiert. Diese Verknüpfung wird in der üblichen Form zweistelliger Rechenoperationen notiert,
Die Verknüpfung 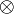 kann als Produktoperation interpretiert werden. Die Produktoperation
kann als Produktoperation interpretiert werden. Die Produktoperation 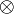 ist eine bilineare Abbildung. Den Vektoren v und w wird ein Tensorprodukt zugeordnet:
ist eine bilineare Abbildung. Den Vektoren v und w wird ein Tensorprodukt zugeordnet:
Für diese Abbildung ergeben sich direkt aus der Bilinearität die folgenden Regeln:
Dabei sind v1 und v2 jeweils ein beliebiges Element des Vektorraumes V; w1 und w2 sind jeweils ein beliebiges Element des Vektorraumes W; λ ist ein beliebiges Element des Grundkörpers K.
Im Allgemeinen nichts miteinander zu tun haben jedoch
selbst wenn V = W ist; andernfalls gehören sie sogar unterschiedlichen Vektorräumen an.
Diese Regeln sehen aus wie Distributivgesetze bzw. Assoziativgesetze der Multiplikation; auch daher der Name Tensorprodukt. Damit das Tensorprodukt diese Eigenschaften haben kann, muss der Raum der Tensorprodukte selbst wieder ein Vektorraum sein. Das heißt aber insbesondere, dass beliebige Summen
in diesem Tensorproduktvektorraum gebildet werden können. Diese stellen die allgemeinste Form eines Tensors 2. Stufe dar, jedoch kann mit den angegebenen Rechenregeln derselbe Tensor durch verschiedene Summen von Tensorprodukten dargestellt werden.
Da die Menge der Tensorprodukte 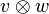 wieder einen Vektorraum über dem Körper K bildet, kann ein Tensor der Form
wieder einen Vektorraum über dem Körper K bildet, kann ein Tensor der Form 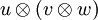 gebildet werden. u ist dabei ein Vektor aus einem weiteren Vektorraum U über K. Man kann zeigen, dass es auf die Reihenfolge der Produktbildung nicht ankommt, also
gebildet werden. u ist dabei ein Vektor aus einem weiteren Vektorraum U über K. Man kann zeigen, dass es auf die Reihenfolge der Produktbildung nicht ankommt, also 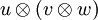 =
= 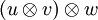 . Durch Fortsetzung ist es möglich, Tensorprodukte mit beliebig vielen Faktoren zu definieren:
. Durch Fortsetzung ist es möglich, Tensorprodukte mit beliebig vielen Faktoren zu definieren:
Jeder Tensor kann als Summe reiner Tensorprodukte dargestellt werden, insbesondere als Linearkombination der Tensorprodukte der Basisvektoren,
Dabei ist 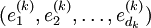 eine Basis des Vektorraums V(k), aus welchem der k-te Faktor des Tensorproduktes stammt. Fasst man die Koeffizienten dieser Basisdarstellung zu einem mehrfach indizierten Tupel zusammen, so entsteht die obige Tensordarstellung.
eine Basis des Vektorraums V(k), aus welchem der k-te Faktor des Tensorproduktes stammt. Fasst man die Koeffizienten dieser Basisdarstellung zu einem mehrfach indizierten Tupel zusammen, so entsteht die obige Tensordarstellung.
Beispielsweise kann man in einem Tensor 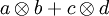 die vorkommenden Vektoren in ihren Basen darstellen,
die vorkommenden Vektoren in ihren Basen darstellen,
und erhält die Basisdarstellung
Tensoren als multilineare Abbildung
Tensoren T lassen sich als multilineare Abbildungen in einen Vektorraum W interpretieren:
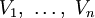 und W sind jeweils Vektorräume über dem gemeinsamen Körper K (W selbst kann beispielsweise wieder ein Tensorprodukt sein).
und W sind jeweils Vektorräume über dem gemeinsamen Körper K (W selbst kann beispielsweise wieder ein Tensorprodukt sein). 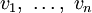 seien jeweils beliebige Vektoren aus den entsprechenden Vektorräumen
seien jeweils beliebige Vektoren aus den entsprechenden Vektorräumen 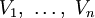 .
.
Multilinear bedeutet, dass die Abbildung linear in jedem ihrer Argumente sein muss. Sei i ein Index, der von 1 bis n läuft. xi und yi seien zwei beliebige Vektoren aus dem Vektorraum Vi. λ sei ein beliebiges Element des Körpers K. Dann muss für alle i = 1,...,n gelten:
Der Zusammenhang mit der Definition des Tensors als Tensorprodukt ergibt sich durch folgende Identifikation:
Koordinaten eines Tensors
Jeder der Vektorräume 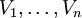 besitzt eine Basis. Als Basisvektoren der jeweiligen Vektorräume werden
besitzt eine Basis. Als Basisvektoren der jeweiligen Vektorräume werden 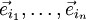 bezeichnet. Der erste Index unterscheidet dabei die Basisvektoren des jeweiligen Vektorraums, der Vektorraum selbst wird mit dem zweiten Index gekennzeichnet.
bezeichnet. Der erste Index unterscheidet dabei die Basisvektoren des jeweiligen Vektorraums, der Vektorraum selbst wird mit dem zweiten Index gekennzeichnet. 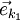 stellt also den k-ten Basisvektor des Vektorraums V1 dar. Der Vektorraum V1 hat eine bestimmte Dimension d, so dass er d Basisvektoren
stellt also den k-ten Basisvektor des Vektorraums V1 dar. Der Vektorraum V1 hat eine bestimmte Dimension d, so dass er d Basisvektoren 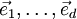 besitzt. Das gilt entsprechend für alle Vektorräume
besitzt. Das gilt entsprechend für alle Vektorräume 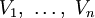 .
.
Die Koordinaten eines Tensors sind folgendermaßen definiert:
Handelt es sich bei dem Tensor T um Elemente eines mehrdimensionalen Vektorraums W, so ist nach obiger Definition 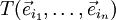 ein Element aus diesem Vektorraum W. T kann wiederum nach den Basisvektoren dieses Vektorraums W entwickelt werden. Dadurch können die Koordinaten als rein skalare Größen dargestellt werden. Die Koordinaten erhalten in dieser Darstellung einen weiteren Index i.
ein Element aus diesem Vektorraum W. T kann wiederum nach den Basisvektoren dieses Vektorraums W entwickelt werden. Dadurch können die Koordinaten als rein skalare Größen dargestellt werden. Die Koordinaten erhalten in dieser Darstellung einen weiteren Index i.
Jeder beliebige Vektor 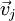 des Vektorraums Vj lässt sich als Linearkombination seiner Basisvektoren darstellen, so dass gilt:
des Vektorraums Vj lässt sich als Linearkombination seiner Basisvektoren darstellen, so dass gilt:
Mit vij werden die Koordinaten des Vektors 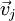 bezeichnet. Die Koordinaten des Vektors
bezeichnet. Die Koordinaten des Vektors  sind Skalare aus dem Körper K. Für die Abbildung der Vektoren
sind Skalare aus dem Körper K. Für die Abbildung der Vektoren 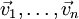 unter dem Tensor T gilt also ganz allgemein:
unter dem Tensor T gilt also ganz allgemein:
Basiswechsel und Koordinatentransformation
Seien 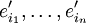 und
und 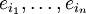 jeweils unterschiedliche Basen der Vektorräume
jeweils unterschiedliche Basen der Vektorräume 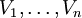 . Jeder Vektor, also auch jeder Basisvektor
. Jeder Vektor, also auch jeder Basisvektor 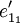 kann als Linearkombination der Basisvektoren
kann als Linearkombination der Basisvektoren 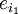 dargestellt werden. Der Basisvektor
dargestellt werden. Der Basisvektor 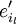 werde dargestellt durch:
werde dargestellt durch:
Die Größen 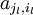 bestimmen also die Basistransformation zwischen den Basen
bestimmen also die Basistransformation zwischen den Basen 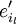 und
und 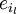 . Das gilt für alle
. Das gilt für alle 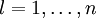 .
.
Ferner stelle 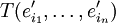 die Koordinaten
die Koordinaten 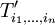 des Tensors T in der Basis
des Tensors T in der Basis 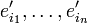 dar. Dann ergibt sich für das Transformationsverhalten der Tensorkoordinaten:
dar. Dann ergibt sich für das Transformationsverhalten der Tensorkoordinaten:
Wichtig: Es wird in der Regel zwischen den Koordinatendarstellung des Tensors 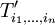 und den Transformationsmatrizen
und den Transformationsmatrizen 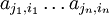 unterschieden. Die Transformationsmatrix
unterschieden. Die Transformationsmatrix 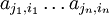 ist zwar eine indizierte Größe aber kein Tensor. Im euklidischen Raum sind das Drehmatrizen und in der speziellen Relativitätstheorie z.B. Lorentz-Transformationen, die sich auch als „Drehungen“ in einem vierdimensionalen Minkowskiraum auffassen lassen (man spricht in diesem Fall auch von Vierertensoren und Vierervektoren).
ist zwar eine indizierte Größe aber kein Tensor. Im euklidischen Raum sind das Drehmatrizen und in der speziellen Relativitätstheorie z.B. Lorentz-Transformationen, die sich auch als „Drehungen“ in einem vierdimensionalen Minkowskiraum auffassen lassen (man spricht in diesem Fall auch von Vierertensoren und Vierervektoren).
Beispiele von wichtigen Tensoren in der Physik
Das Kronecker-Delta δ ist ein Tensor zweiter Stufe. Es ist ein Element von 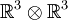 ; es ist also eine lineare Abbildung
; es ist also eine lineare Abbildung 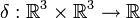 . Lineare Abbildungen sind durch die Wirkung auf die Basisvektoren eindeutig bestimmt. So ist das Kronecker-Delta eindeutig durch
. Lineare Abbildungen sind durch die Wirkung auf die Basisvektoren eindeutig bestimmt. So ist das Kronecker-Delta eindeutig durch
bestimmt.
Das Levi-Civita-Symbol 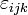 , das zur Berechnung des Kreuzprodukts zwischen Vektoren gebraucht wird, ist ein Tensor dritter Stufe. Es gilt
, das zur Berechnung des Kreuzprodukts zwischen Vektoren gebraucht wird, ist ein Tensor dritter Stufe. Es gilt 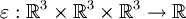 . Man schreibt
. Man schreibt 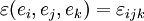 .
.
Beide Symbole werden häufig verwendet, um Symmetrieeigenschaften von Tensoren zu untersuchen. Das Kronecker-Delta ist symmetrisch bei Vertauschungen der Indizes, das Levi-Civita-Symbol antisymmetrisch, so dass man mit ihrer Hilfe Tensoren in symmetrische und antisymmetrische Anteile zerlegen kann. In Tensordarstellungen z. B. der Drehgruppe SO(n) erhält man so eine Zerlegung in irreduzible Darstellungen (das heißt Unterräume der Tensorräume, die bei Drehungen in sich transformieren und dabei keine unter Drehungen invariante Unterräume haben).
Ein Beispiel für einen Tensor 2. Stufe ist auch der oben diskutierte Trägheitstensor. In der Elastizitätstheorie verallgemeinert man die Hooke'sche Gleichung über den Zusammenhang zwischen Kräften und zugehörigen Dehnungen und Verzerrungen in einem elastischen Medium ebenfalls mit Hilfe der Tensorrechnung durch Einführung des Verzerrungstensors (der Verzerrungen, Deformationen beschreibt) und Spannungstensors (der die die Deformationen verursachenden Kräfte beschreibt, siehe Kontinuumsmechanik). Der Energie-Impuls-Tensor Tαβ und der elektromagnetische Feldstärketensor Fαβ (als Beispiel eines Feldstärketensors) in der Relativitätstheorie sind Tensoren zweiter Stufe auf der vierdimensionalen Basis der Raumzeit. In der Multipol-Analyse physikalischer Felder ist das Dipolmoment ein Vektor und das Quadrupolmoment ein Tensor 2. Stufe.
In der Allgemeinen Relativitätstheorie werden Differentialgleichungen für den metrischen Tensor aufgestellt, die den riemannschen Krümmungstensor mit dem Energie-Impuls-Tensor in Beziehung setzen. Dabei wird der metrische Tensor als ortsabhängige Funktion betrachtet ("Tensorfeld") und der für die Differentialgeometrie entwickelte Formalismus der Analysis auf Mannigfaltigkeiten verwendet (Tensoranalysis) mit dem grundlegenden Begriff der kovarianten Ableitung.
Kovariante und Kontravariante Tensoren
Die Vektoren eines Vektorraumes V sind "Tensoren der Stufe 1". Ihr Koordinatentupel 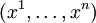 bzgl. einer gegebenen Basis
bzgl. einer gegebenen Basis 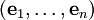 , n = dimV, wird als kontravarianter Vektor bzw. Tensor bezeichnet.
, n = dimV, wird als kontravarianter Vektor bzw. Tensor bezeichnet.
Die Koordinaten xi eines kontravarianten Tensors tragen konventionsgemäß einen hochgestellten Index i.
Die Vektoren des dualen Vektorraums V * , d.h. lineare Funktionale, sind ebenfalls Vektoren, das heißt Tensoren der Stufe 1. Koordinaten eines solchen Vektors sind die Werte des Funktionals auf der Basis des Vektorraums. Das Tupel dieser Werte wird als kovariante Vektoren bzw. Tensoren bezeichnet.
In vielen Anwendungen ist dabei K der Körper der reellen Zahlen.
Die Basisvektoren des dualen Vektorraums V * seien gegeben durch:
mit der Dualitätsrelation 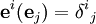 mit dem Kronecker-Delta.
mit dem Kronecker-Delta.
Für einen beliebigen Vektor 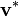 des Dualraums gibt es folgende Koordinatendarstellung:
des Dualraums gibt es folgende Koordinatendarstellung:
Die Koordinaten 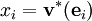 eines kovarianten Tensors tragen konventionsgemäß einen tiefgestellten Index i.
eines kovarianten Tensors tragen konventionsgemäß einen tiefgestellten Index i.
Die Vektoren v können mit den Vektoren v** des zugehörigen Bidualraumes V** identifiziert werden. Denn es existiert eine Bijektion zwischen den Elementen des Vektorraums V und des zugehörigen Bidualraums V**. Der Bidualraum umfasst die linearen Abbildungen von v* in K, also
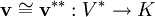
Man definiert einen Tensor vom Grad (r, s) als multilineare Abbildung mit r Argumenten v1,...,vr und s Argumenten λ1,...,λs. Die Argumente v1,...,vr sind Elemente eines Vektorraumes V und λ1,...,λs Argumente des zum Vektorraum gehörenden Dualraumes V * .
Der Tensor hat dann die Form
Die Summe r + s heißt Stufe oder Rang des Tensors.
Je nachdem, ob die Argumente aus einem Vektorraum sind oder aus dessen Dualraum, wird der Tensor als kovariant oder kontravariant bezeichnet. Im obigen Fall liegt ein r-fach kovarianter, s-fach kontravarianter Tensor vor.
In metrischen Vektorräumen (z.B. in den Anwendungen in der Relativitätstheorie) ist durch die Metrik in natürlicher Weise ein dualer Vektorraum gegeben und der Übergang von kontravarianten zu kovarianten Vektoren bzw. Komponenten eines Tensors wird durch den metrischen Tensor 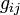 bewerkstelligt (siehe auch Indexdarstellungen der Relativitätstheorie). Im Fall der allgemeinen Relativitätstheorie ist diese Metrik sogar meist von Punkt zu Punkt verschieden, also eine Funktion des Ortes – man spricht dann von Tensorfeldern
bewerkstelligt (siehe auch Indexdarstellungen der Relativitätstheorie). Im Fall der allgemeinen Relativitätstheorie ist diese Metrik sogar meist von Punkt zu Punkt verschieden, also eine Funktion des Ortes – man spricht dann von Tensorfeldern 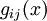 . Man kann dann von ko- zu kontravarianten Vektoren bzw. Koordinaten (und umgekehrt) durch Anwendung des metrischen Tensors übergehen:
. Man kann dann von ko- zu kontravarianten Vektoren bzw. Koordinaten (und umgekehrt) durch Anwendung des metrischen Tensors übergehen:
In der Relativitätstheorie verwendet man dabei statt der euklidischen Metrik diejenige des Minkowskiraumes. Noch allgemeinere Metriken (allerdings mit derselben Signatur wie die Minkowski-Metrik) werden in der Allgemeinen Relativitätstheorie verwendet.
Tensoroperationen – Tensorprodukt und Verjüngung
Das oben definierte Produkt zweier Tensoren wird in der Indexdarstellung gebildet, indem die beiden Indextupel in der Reihenfolge ihres Auftretens unter Beibehaltung aller hoch- und Tiefstellungen zum Indextupel eines neuen Tensors aneinandergekoppelt werden. Dabei sind die Indizes beider Tensoren als voneinander verschieden zu betrachten und notieren. Die Komponenten des neuen Tensors ergeben als Produkte der Komponenten der alten Tensoren, deren Indexbelegungen die Indexbelegung der Komponente des neuen Tensors ergeben. Zum Beispiel ist das Produkt von Tensoren Aij und Bijk ein Tensor fünfter Stufe 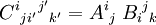 . Dessen Komponente C21321 ist das Produkt der Komponenten A21 und B321.
. Dessen Komponente C21321 ist das Produkt der Komponenten A21 und B321.
Meist wird die von Einstein eingeführte Summationskonvention verwendet: über jeden Index, der in einem Tensorausdruck genau zweimal vorkommt, und zwar einmal als tief- und einmal als hochgestellter Index, wird automatisch summiert. Es ist also
von nun an eine Kurzschreibweise für
Diese Operation heißt Verjüngung des Tensors. Es ist also Aii ein Skalar, welcher die Summe aller Diagonalelemente einer mit A assoziierten Matrix ist, die sogenannte "Spur". Biji ist nicht definiert, Bijj ein Tensor erster Stufe.
Haben in einem Tensorprodukt die aneinanderliegenden äußeren Enden der Indextupel unterschiedliche Stellung, aber gleiche Indexdimension, so können diese im Produkt gleichgesetzt und damit automatisch heraussummiert werden. Diese Kombination aus Produkt und Verjüngung nennt sich Überschieben der Tensoren. Beispielsweise kann Aij Bijk zu einem Tensor dritter Stufe 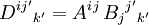 überschoben werden. Ein Spezialfall ist das Matrix-Matrix-Produkt
überschoben werden. Ein Spezialfall ist das Matrix-Matrix-Produkt 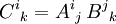 . Ein Tensor höherer Stufe kann auch mehrfach mit Vektoren überschoben werden, bis alle Indizes aufgebraucht sind, F = BijkCkDjEi ist ein Skalar, der sich aus der Auswertung von B als Multilinearform ergibt.
. Ein Tensor höherer Stufe kann auch mehrfach mit Vektoren überschoben werden, bis alle Indizes aufgebraucht sind, F = BijkCkDjEi ist ein Skalar, der sich aus der Auswertung von B als Multilinearform ergibt.
Tensorbegriff der Mathematik
Unterschiedliche Betrachtungsweisen
In der Physik wird „Tensor“ oft als Abkürzung für Tensorfeld verwendet. Ein Tensorfeld ist eine Abbildung, die jedem Punkt des Raums (allgemeiner: einer Mannigfaltigkeit) einen Tensor zuordnet; jede physikalische Feldtheorie handelt von Tensorfeldern. Das mag im ersten Moment verwirrend erscheinen. Dahinter verbergen sich nur unterschiedliche Blickrichtungen auf die gleichen Objekte, erläutert am Beispiel von Vektorfeldern:
Welcher Blickwinkel gerade verwendet wird, ergibt sich aus dem Kontext.
Universaldefinition des Tensorprodukts
Als Tensorprodukt der Vektorräume V und W, d.h. als Vektorraum, in welchem die Tensorprodukte von Vektoren aus V und W „leben“, wird jeder Vektorraum X (über dem gemeinsamen Skalarenkörper von V und W) bezeichnet, zu dem es eine bilineare Abbildung 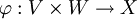 gibt, die die folgende universelle Eigenschaft erfüllt:
gibt, die die folgende universelle Eigenschaft erfüllt:
Gibt es einen solchen Vektorraum, so ist er (bis auf Isomorphie) eindeutig. Es wird 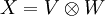 und
und 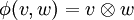 notiert. Die universelle Eigenschaft kann also als
notiert. Die universelle Eigenschaft kann also als 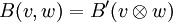 geschrieben werden. Zur Konstruktion solcher Produkträume sei auf den Artikel Tensorprodukt verwiesen.
geschrieben werden. Zur Konstruktion solcher Produkträume sei auf den Artikel Tensorprodukt verwiesen.
Tensor als Element des Tensorproduktes
In der Mathematik sind Tensoren Elemente von Tensorprodukten.
Es sei K ein Körper, also beispielsweise 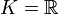 oder
oder 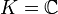 , und es seien
, und es seien 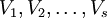 Vektorräume über K.
Vektorräume über K.
Das Tensorprodukt 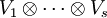 von
von 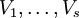 ist ein K-Vektorraum, dessen Elemente Summen von Symbolen der Form
ist ein K-Vektorraum, dessen Elemente Summen von Symbolen der Form
sind. Dabei gelten für diese Symbole die folgenden Rechenregeln:
Die Tensoren der Form 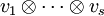 heißen elementar. Jeder Tensor lässt sich als Summe von elementaren Tensoren schreiben, aber diese Darstellung ist außer in trivialen Fällen nicht eindeutig, wie man an der ersten der beiden Rechenregeln sieht.
heißen elementar. Jeder Tensor lässt sich als Summe von elementaren Tensoren schreiben, aber diese Darstellung ist außer in trivialen Fällen nicht eindeutig, wie man an der ersten der beiden Rechenregeln sieht.
Ist 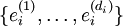 eine Basis von Vi (für
eine Basis von Vi (für 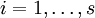 ;
; 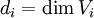 ), so ist
), so ist
eine Basis von 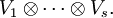 Die Dimension von
Die Dimension von 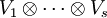 ist also das Produkt der Dimensionen der einzelnen Vektorräume
ist also das Produkt der Dimensionen der einzelnen Vektorräume 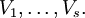
Tensorprodukte und Multilinearformen
Der Dualraum von 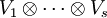 kann mit dem Raum der s-Multilinearformen
kann mit dem Raum der s-Multilinearformen
identifiziert werden:
Sind alle betrachteten Vektorräume endlichdimensional, so kann man
miteinander identifizieren, d.h. Elemente von 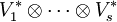 entsprechen s-Multilinearformen auf
entsprechen s-Multilinearformen auf 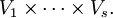
(r,s)-Tensoren
Es sei V ein fester endlichdimensionaler Vektorraum über K.
Elemente von
heißen (r,s)-Tensoren oder Tensoren der Stufe (r,s).
Beispielsweise sind (0,0)-Tensoren Skalare, (0,1)-Tensoren Elemente des Vektorraums und (1,0)-Tensoren Linearformen auf V. (1,1)-Tensoren können mit Endomorphismen von V und (2,0)-Tensoren mit Bilinearformen auf V identifiziert werden (siehe unten).
Für (r,s)-Tensoren gibt es drei wichtige Konstruktionen:
Es sei g ein (2,0)-Tensor und 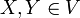 zwei Vektoren. Dann ist
zwei Vektoren. Dann ist
ein (2,2)-Tensor, der durch zweimalige Spurbildung ein Element von K liefert. Da alle diese Konstruktionen multilinear sind, definiert g also eine Bilinearform
(2,0)-Tensoren können also mit Bilinearformen identifiziert werden.
Beispiele
In der Differentialgeometrie spielen Tensorfelder eine wichtige Rolle: Ist M eine differenzierbare Mannigfaltigkeit, so ist ein Tensorfeld auf M eine Abbildung, die jedem Punkt einen Tensor zuordnet. Meist werden auch noch gewisse Differenzierbarkeitseigenschaften gefordert.
Beispiele sind:
Siehe auch: Tensoralgebra, äußere Algebra, symmetrische Algebra.
Ko- und Kontravarianz als Eigenschaften von Abbildungen
Sei V ein fester K-Vektorraum und W ein beliebiger weiterer K-Vektorraum. Eine lineare Abbildung 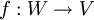 heißt kovariant bezüglich V, eine lineare Abbildung
heißt kovariant bezüglich V, eine lineare Abbildung 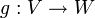 heißt kontravariant in V.
heißt kontravariant in V.
Eine Quelle der Verwirrung über diese Begriffe ist, dass in der Physik und älteren Lehrbüchern davon gesprochen wird, dass sich die Matrizen dieser Abbildungen ko- bzw. kontravariant unter Basiswechsel transformieren. Jedoch kehren sich dabei die Zuordnungen um – eine kovariante Abbildung hat eine Matrix, die kontravariant bzgl. Basiswechsel ist und umgekehrt.
Grundlegende Beispiele:
Tensorprodukte eines Vektorraums und Symmetrie
Man kann das Tensorprodukt 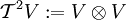 eines Vektorraumes V mit sich selbst bilden. Ohne weiteres Wissen über den Vektorraum kann ein Automorphismus des Tensorprodukts definiert werden, der darin besteht, in den reinen Produkten
eines Vektorraumes V mit sich selbst bilden. Ohne weiteres Wissen über den Vektorraum kann ein Automorphismus des Tensorprodukts definiert werden, der darin besteht, in den reinen Produkten 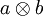 die Faktoren zu vertauschen,
die Faktoren zu vertauschen,
Das Quadrat dieser Abbildung ist die Identität, woraus folgt, dass es Eigenvektoren zum Eigenwert 1 und zum Eigenwert -1 gibt.
Mittels 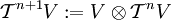 können Tensorpotenzen von V beliebiger Stufe gebildet werden. Entsprechend können weitere paarweise Vertauschungen definiert werden. Nur sind diese nicht mehr voneinander unabhängig. So lässt sich jede Vertauschung der Stellen j und k auf Vertauschungen mit der ersten Stelle zurückführen.
können Tensorpotenzen von V beliebiger Stufe gebildet werden. Entsprechend können weitere paarweise Vertauschungen definiert werden. Nur sind diese nicht mehr voneinander unabhängig. So lässt sich jede Vertauschung der Stellen j und k auf Vertauschungen mit der ersten Stelle zurückführen.
Anwendungen
Tensoren und Tensorfelder werden in verschiedenen Teilgebieten der Mathematik und Physik angewandt. Diese Anwendungen sind von sehr unterschiedlicher Komplexität:
Man muss deshalb damit rechnen, dass Tensoren in verschiedenen Anwendungsgebieten verschieden definiert, verschieden notiert und verschieden gehandhabt werden.
Wichtige Anwendungsgebiete umfassen:
Literatur
Weblinks
Wikimedia Foundation.