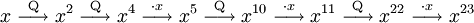ModPower

Die binäre Exponentiation ist eine effiziente Methode zur Berechnung von natürlichen Potenzen, also Ausdrücken der Form x^k mit einer natürlichen Zahl k.

Dieser Algorithmus wurde bereits um ca. 200 v. Chr. in Indien entdeckt und ist in einem Werk namens Chandah-sûtra niedergeschrieben.

Motivation

Um z = x⁴ zu berechnen, kann man entweder 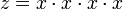$z = x \cdot x \cdot x \cdot x$ ausrechnen (drei Multiplikationen) oder 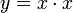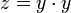$y = x \cdot x$, $z = y \cdot y$ (zwei Multiplikationen), also z = (x²)².

Ebenso können auch andere ganzzahlige Potenzen durch „fortgesetztes Quadrieren und gelegentliches Multiplizieren“ effizient berechnet werden.

Dieses Einsparen von Multiplikationen funktioniert sowohl für reelle Zahlen als auch für reellwertige Matrizen und beliebige andere Halbgruppen.

Algorithmus

• Umwandlung von k in die zugehörige Binärdarstellung.
• Ersetzen jeder 0 durch Q und jeder 1 durch QM.
• Streichen des führenden QM-Paares.
• Nun wird Q als Anweisung zum Quadrieren und M als Anweisung zum Multiplizieren aufgefasst.
• Somit bildet die resultierende Zeichenkette von links nach rechts gelesen eine Vorschrift zur Berechnung von x^k.

Beispiel

Sei k = 23. Die Binärdarstellung von 23 lautet 10111. Daraus ergibt sich nach den Ersetzungen QM Q QM QM QM. Nach dem Streichen des führenden QM-Paares hat man Q QM QM QM. Daraus können wir nun ablesen, dass der Rechenvorgang folgendermaßen auszusehen hat: "quadriere, quadriere, multipliziere mit x, quadriere, multipliziere mit x, quadriere, multipliziere mit x".

Formal sieht das Ganze so aus: 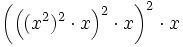$\left( \left( (x^2)^2 \cdot x \right)^2 \cdot x \right)^2 \cdot x$ bzw. sukzessive geschrieben:

$x \;\stackrel{\mathrm Q}\longrightarrow\; x^2 \;\stackrel{\mathrm Q}\longrightarrow\; x^4 \;\stackrel{\cdot x} \longrightarrow\; x^5 \;\stackrel{\mathrm Q}\longrightarrow\; x^{10} \;\stackrel{\cdot x} \longrightarrow\; x^{11} \;\stackrel{\mathrm Q}\longrightarrow\; x^{22} \;\stackrel{\cdot x}\longrightarrow\; x^{23}$

Man sieht am Beispiel, dass man sich mit Hilfe der binären Exponentiation einige Rechenschritte sparen kann. Anstatt von 22 Multiplikationen werden nur mehr 7 benötigt, indem man viermal quadriert und dreimal mit x multipliziert.

Alternativer Algorithmus

Man kann das Verfahren für eine Berechnung von Hand auch so gestalten, dass man zunächst die Basis oft genug quadriert und anschließend die richtigen Zahlen miteinander multipliziert. Dann ähnelt es der russischen Bauernmultiplikation, welche die Multiplikation zweier Zahlen auf das Verdoppeln und Addieren von Zahlen zurückführt.

Dazu schreibt man den Exponenten links und die Basis rechts. Der Exponent wird schrittweise halbiert (das Ergebnis wird abgerundet) und die Basis schrittweise quadriert. Man streicht die Zeilen mit geradem Exponenten. Das Produkt der nichtgestrichenen rechten Zahlen ist die gesuchte Potenz.

Beispiel

218
18	2
9	4
4	16
2	256
1	65.536
Ergebnis	262.144 (= 4 · 65.536)

Binäre modulo-Exponentiation

Beim Rechnen modulo einer natürlichen Zahl ist eine leichte Modifikation anwendbar, die verhindert, dass die berechneten Zahlen zu groß werden: Man bildet nach jedem Quadrieren den Rest.

Beispiel

218 mod 39
18	2
9	4
4	16
2	22 (= 256 mod 39)
1	16 (= 484 mod 39)
Ergebnis	25 (= 4 · 16 mod 39 = 218 mod 39)

ähnliche Algorithmen

Die Binäre Exponentiation muss nicht notwendig die "multiplikationssparendste" Berechnungsart einer Potenz sein. Um beispielsweise z = x¹⁵ zu berechnen, kann man entweder gemäß binärer Exponentiation

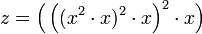$z = \Big( \left((x^2 \cdot x)^2 \cdot x \right)^2 \cdot x \Big)$ berechnen (6 Multiplikationen), oder

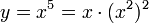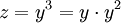$y = x^5 = x \cdot (x^2)^2$, $z = y^3 = y \cdot y^2$ (5 Multiplikationen).

Literatur

• Donald E. Knuth: The Art of Computer Programming. Vol 2. Addison Wesley, 1998 (Seite 399)
• Jörg Arndt, Christoph Haenel: Pi. Algorithmen, Computer, Arithmetik. 2. Auflage. Springer, Berlin 2000 (Seite 120-121) ISBN 3-540-66258-8