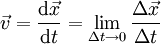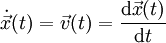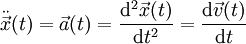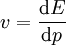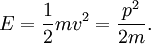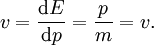Momentangeschwindigkeit

Physikalische Größe
Name	Geschwindigkeit
Formelzeichen der Größe	v, u, w, c
Abgeleitet von	lat. velocitas
Größen- und Einheiten- system Einheit Dimension SI Meter pro Sekunde (m·s-1) L·T-1 CGS Zentimeter pro Sekunde (cm·s-1) L·T-1 Planck Lichtgeschwindigkeit (c) c

Unter der Geschwindigkeit (Formelzeichen: v, von lat. velocitas) eines Objekts versteht man die von ihm zurückgelegte Wegstrecke s pro Zeit t. Mathematisch entspricht die Geschwindigkeit der Ableitung des Ortes nach der Zeit.

Definition

Die Definition der Geschwindigkeit als Zeitableitung des Ortes lässt sich in vier Schritten nachvollziehen;

1. Gesamtdurchschnittsgeschwindigkeit: $\bar v={x \over t}$
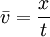
2. Durchschnittsgeschwindigkeit in einem bestimmten Abschnitt: $\bar v={\Delta x \over \Delta t}= { x_2-x_1 \over t_2-t_1 }$
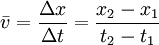
3. Momentangeschwindigkeit (= differentielle Abschnittsgeschwindigkeit): $v={\mathrm{d}x \over \mathrm{d}t} = \lim_{\Delta t \to 0}{\Delta x \over \Delta t}$
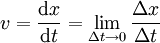
4. Eine Strecke hat immer eine Richtung und ist daher ein Vektor. Aus diesem Grunde ist auch die Geschwindigkeit eine vektorielle Größe. Die exakte Definition lautet deshalb:

$\vec {v}={\mathrm{d}\vec {x} \over \mathrm{d}t} = \lim_{\Delta t \to 0}{\Delta \vec {x} \over \Delta t}$

Im Englischen wird (besonders unter Mathematikern und Physikern) gelegentlich zwischen velocity (vektorielle Geschwindigkeit) und speed (Betrag der Geschwindigkeit) unterschieden. Auch im deutschen Sprachraum wird teilweise dieser Unterschied gemacht: Für velocity (vektorielle Geschwindigkeit: 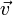$\vec {v}$) wird dann der Begriff Geschwindigkeit verwendet und für speed (Betrag der Geschwindigkeit: v) der Begriff Tempo oder Schnelligkeit.
Ein Beispiel: Auf einer Kreisbahn kann ein Auto eine konstante Schnelligkeit, aber nie eine konstante Geschwindigkeit haben.

Ist der Ort x eine Funktion der Zeit t in der Form x = x(t), so ergibt sich die Geschwindigkeit v(t) durch Ableiten des Ortes nach der Zeit, mit

$\dot \vec {x}(t)=\vec {v}(t)={\mathrm{d}\vec {x}(t) \over \mathrm{d}t}$

wobei man in der Physik Ableitungen nach der Zeit üblicherweise als 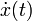$\dot x(t)$ schreibt.

Die zeitliche Änderung der Geschwindigkeit ist die Beschleunigung, die ebenfalls ein Vektor ist, mit

$\ddot \vec {x}(t) = \vec {a}(t)={\mathrm{d^2}\vec {x}(t) \over \mathrm{d}t^2}={\mathrm{d}\vec {v}(t) \over \mathrm{d}t}$

Ebenfalls lässt sich die Geschwindigkeit als Ableitung der Energie nach dem Impuls definieren, mit

$v = \frac{\mathrm{d}E}{\mathrm{d}p}$

Beispiel: Die kinetische Energie in der klassischen Mechanik ist

$E = \frac{1}{2} m v^2 = \frac{p^2}{2m}.$

Die Ableitung ist dann

$v = \frac{\mathrm{d}E}{\mathrm{d}p} = \frac{p}{m} = v.$

Die Geschwindigkeiten in einem strömenden Medium können als Vektorfeld aufgefasst werden.

Bei astronomischen Objekten, wie Planeten, Kometen, oder Satelliten nennt man die Geschwindigkeit traditionell Bahngeschwindigkeit, oder Orbitalgeschwindigkeit. Dies geschieht, um die Geschwindigkeit längs der Bahn eindeutig von der Winkelgeschwindigkeit abzugrenzen, mit der der Himmelskörper über den Nachthimmel zieht.

Siehe auch Keplersche Gesetze für weitere Informationen hierzu.

Einheiten

SI-Einheit der Geschwindigkeit ist Meter pro Sekunde (m/s). Eine weitere gebräuchliche Einheit der Geschwindigkeit ist Kilometer pro Stunde (km/h).

In der Alltagssprache (auch im Duden) wird auch die Bezeichnung „Stundenkilometer“ verwendet, welche im Sinne von „stündlichen Kilometern“ gemeint ist. Da es jedoch in der Physik Konvention ist, dass eine derartige Zusammensetzung für eine Multiplikation der aufgeführten Einheiten steht, würde „Stundenkilometer“ für die Einheit „km×h“ statt „km/h“ stehen. Deshalb sollte der Ausdruck „Stundenkilometer“ vermieden werden. Im Alltag führt der Begriff nicht zu Missverständnissen, da es keine Größe mit der Einheit „km×h“ gibt. In der geschriebenen Sprache sollte man aber insbesondere bei der Abkürzung „km/h“ den Divisionsstrich nicht weglassen.

Als nicht metrische Einheit wird vor allem in den USA und einigen anderen englischsprachigen Ländern Meilen pro Stunde (mph) benutzt. In der See- und Luftfahrt ist außerdem die Einheit Knoten (kn) gebräuchlich; ein Knoten ist eine Seemeile pro Stunde. Vertikalgeschwindigkeiten in der motorisierten Luftfahrt werden in der Regel in Fuß pro Minute angegeben.

Fast nur in der Luftfahrt wird das Mach verwendet, das keine absolute Größe hat, sondern das Verhältnis der Geschwindigkeit zur lokalen Schallgeschwindigkeit angibt. Die Schallgeschwindigkeit ist stark temperaturabhängig aber nicht luftdruckabhängig. Der Grund für die Nutzung dieser Zahl ist, dass aerodynamische Effekte von ihr abhängen. Beim Erreichen der Schallgeschwindigkeit ändert sich das Strömungsverhalten. Propellermaschinen können beispielsweise nicht schneller als der Schall fliegen, sondern nur einen bestimmten Bruchteil der Schallgeschwindigkeit erreichen, gleichgültig, wie groß diese absolut ist.

Umrechnung gebräuchlicher Geschwindigkeitseinheiten:

• 1 kn = 0,5144 m/s = 1,852 km/h (= 1 Seemeile/h);
• 1 m/s = 1,944 kn = 3,6 km/h (exakt) = 2,237 mph (Kehrwert: 1 km/h = 5/18 m/s = 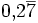$0{,}2\overline{7}$ ≈ 0,278)
• 1 km/h = 0,540 kn = 0,2778 m/s = 0,6214 mph;
• 1 mph = 0,8690 kn = 0,44704 m/s (exakt) = 1,609344 km/h (exakt);
• 100 ft/min = 0,508 m/s (exakt);
• c = 299.792.458 m/s (exakt) = 582.749.918 kn = 670.616.629 mph = 1.079.252.848,8 km/h. (exakt)

Die Lichtgeschwindigkeit c ist eine wichtige Naturkonstante der Physik. Mit dieser Geschwindigkeit breiten sich elektromagnetische Wellen, also auch das Licht, im Vakuum aus.

Andere Bedeutungen des Begriffs

Der Begriff Geschwindigkeit wird umgangssprachlich auch auf zeitliche Veränderungen anderer Größen bezogen. So spricht man beispielsweise von der Geschwindigkeit einer Temperaturänderung oder der Geschwindigkeit, mit der eine Population wächst, sich eine Kultur entwickelt oder ein Mensch seine Meinung ändert.

Verhältnis zu Beschleunigung und Ruck

Die Ableitung des Ortes nach der Zeit ergibt die Geschwindigkeit: $\vec {v}(t)=\dot \vec {x}(t)$

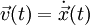
Die zweite Ableitung des Ortes nach der Zeit, also die Ableitung der Geschwindigkeit, ist die Beschleunigung: $\vec {a}(t)=\dot \vec {v}(t)=\ddot \vec {x}(t)$

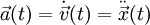
Die dritte Ableitung schließlich, also nunmehr die Ableitung der Beschleunigung nach der Zeit, gibt den Ruck an: $\vec {j}(t)= \dot \vec {a}(t)=\ddot \vec {v}(t) = {\mathrm{d^3}\vec {x}(t)\over \mathrm{d}t^3}$

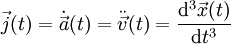
Geschichtliche Anmerkung

Galileo Galilei definierte wohl als Erster die Geschwindigkeit gleichförmig-geradliniger Bewegung geometrisch, und zwar als Proportionalität der vom bewegten Körper zurückgelegten Strecken s zu den dazu benötigten Zeiten t.^[1] Dies entspricht in heutigen Begriffen der Durchschnittsgeschwindigkeit.

Siehe auch

• Größenordnung (Geschwindigkeit)
• Geschwindigkeitsrekord
• Durchsatz
• Datendurchsatz (Informatik)
• Geschwindigkeit (Straßenverkehr)

Einzelnachweise

1. ↑ Galileo Galilei: „Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti alla mecanica ed i movimenti locali“, Leiden 1638

Weblinks

• Versuche und Aufgaben zur Geschwindigkeit