- NASA/NORAD Two Line Elements Format
-
Satellitenbahnelemente sind Zahlen, mit denen sich die Umlaufbahnen (Orbits) und Positionen von Satelliten beschreiben und bestimmen lassen. Sie sind damit eine wichtige Quelle für die unterschiedlichsten Anwendungen in der Raumfahrt.
Die Bahnelemente für die meisten Satelliten werden vom amerikanischen Air Force Space Command zur Verfügung gestellt und von unterschiedlichen Organisationen, wie z. B. NASA oder AMSAT als NASA/NORAD Two Line Elements Format (TLE)[1] verteilt. Hierzu werden die Daten einer Vorhersage-Berechnung mit der tatsächlichen Beobachtung durch Tracking-Stationen auf der Erde abgeglichen und als aktualisierte Bahnelemente über verschiedene Wege (meist Internet) veröffentlicht.
Inhaltsverzeichnis
Die sieben (oder acht) Satellitenbahnelemente
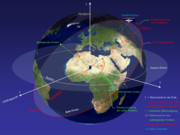
Die folgenden Ausführungen gelten, wenn nicht anders angemerkt, für Satelliten in einer Erdumlaufbahn. Eine graphische Darstellung der Bahnelemente zeigt Abbildung 1.
Ideales Keplersches Modell
Zur Definition der Umlaufbahn und der Position eines Satelliten in dieser Bahn sind sechs Zahlen notwendig. Ein Datensatz dieser Zahlen wird Satellitenbahnelemente genannt. Die Zahlen definieren eine Umlaufbahn durch
-
- ihre elliptische Form,
- ihre Orientierung im Raum und
- die Position des Satelliten
und gelten zu einem bestimmten Zeitpunkt.
Im idealen Keplerschen Modell umlaufen Satellit und Erde das gemeinsame Schwerezentrum auf Ellipsenbahnen konstanter Form und Orientierung. Das Schwerezentrum der beiden Körper liegt dabei im einen Brennpunkte der Ellipse. Für kleine Satelliten ist dieser Punkt praktisch identisch mit dem Erdmassenzentrum. Beim größten natürlichen Satelliten der Erde, dem Mond, liegt dieser Punkt aber im Mittel 4671 km außerhalb des Erdmassenzentrums, d.h. "kurz" unter der Erdoberfläche auf der mondzugewandten Seite.
Perturbation
Die Realität ist allerdings wesentlich komplexer. Abweichungen vom Keplerschen Modell müssen mit Hilfe von Propagations-Modellen [2][3] korrigiert werden. Notwendig werden diese Korrekturen durch die als Perturbation (Bahnstörung) bekannten Unruhen und Störungen der Satellitenbahn. Hervorgerufen werden diese Bahnstörungen unter anderem durch
-
- das unregelmäßige Gravitationsfeld der Erde,
- die Anziehungskraft des Mondes,
- den Strahlungsdruck des Sonnenwindes und
- die Bremswirkung der „hohen“ Atmosphäre und des Magnetfeldes der Erde, deren Ausdehnung wiederum durch die Aktivität der Sonne beeinflusst wird.
Während die Gravitationseinflüsse die Lage und Orientierung der Bahnellipse bis zu mehreren Grad pro Tag verdrehen, führt die Bremswirkung zu einem optionalen achten Bahnelement.
Definitionen
Die grundlegenden Satellitenbahnelemente mit ihren Formelzeichen sind (in Klammern die in der Fachliteratur übliche englische Bezeichnung):
- Epoche
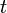 (Epoch)
(Epoch) - Inklination
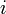 (Inclination)
(Inclination) - Rektaszension des aufsteigenden Knotens
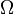 (Right Ascension of Ascending Node)
(Right Ascension of Ascending Node) - Argument des Perigäums
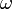 (Argument of Perigee)
(Argument of Perigee) - Numerische Exzentrizität
 (Eccentricity)
(Eccentricity) - Mittlere tägliche Bewegung
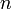 (Mean Motion)
(Mean Motion) - Mittlere Anomalie
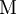 (Mean Anomaly)
(Mean Anomaly) - (optional) Widerstandskoeffizient (Drag)
Epoche
Ein Datensatz von Bahnelementen ist ein „Schnappschuss“ der Satellitenumlaufbahn zu einem bestimmten Zeitpunkt, den man Epoche nennt. Mit dieser Momentaufnahme werden die Zahlenwerte aller Satellitenbahnelemente festgehalten.
Definition: Die Epoche
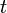 ist eine Zahl, die den Zeitpunkt spezifiziert, wann der „Schnappschuss“ gemacht wurde.
ist eine Zahl, die den Zeitpunkt spezifiziert, wann der „Schnappschuss“ gemacht wurde.Inklination
Jede Umlaufbahn liegt in einer Ebene, die man Bahn- oder Orbitalebene nennt. Die Bahnebene geht immer durch den Erdmittelpunkt (Massezentrum) und ist i.A. zur Äquatorebene der Erde geneigt (Abb. 1).
Definition: Die Inklination (Bahnneigung)
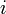 ist der Winkel zwischen der Äquatorebene und der Bahnebene zum Zeitpunkt der Epoche. Vereinbarungsgemäß gilt:
ist der Winkel zwischen der Äquatorebene und der Bahnebene zum Zeitpunkt der Epoche. Vereinbarungsgemäß gilt: 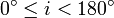 .
.Bahnen mit einer Inklination um 90° werden als "polar" bezeichnet, da der Satellit die Pole der Erde überfliegt. Bahnen mit Inklination deutlich über 90° werden als retrograd bezeichnet, da der Satellit dann die Erde gegen ihren Rotationssinn umläuft.
Rektaszension des aufsteigenden Knotens
Die Inklination für sich alleine reicht nicht aus, um die Lage der Bahnebene im Raum vollständig zu beschreiben. Die Rektaszension
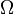 des aufsteigenden Knotens ist die zweite Zahl, die die Bahnebene im Raum endgültig definiert. Sie wird über die Lage der Schnittlinie zwischen Äquatorebene und Bahnebene – die so genannte Knotenlinie – bestimmt (Abb. 1).
des aufsteigenden Knotens ist die zweite Zahl, die die Bahnebene im Raum endgültig definiert. Sie wird über die Lage der Schnittlinie zwischen Äquatorebene und Bahnebene – die so genannte Knotenlinie – bestimmt (Abb. 1).Die Umlaufbahn stößt an zwei Punkten, die auf besagter Knotenlinie liegen, durch die Äquatorebene. Der eine Punkt ist der so genannte aufsteigende Knoten (der Satellit durchstößt dort die Äquatorebene von Süden kommend, „aufsteigend“ nach Norden), der andere ist der so genannte absteigende Knoten (der Satellit durchstößt dort die Äquatorebene von Norden kommend, „absteigend“ nach Süden). Da die Knotenlinie immer in der Äquatorebene liegt und durch den Erdmittelpunkt führt, genügt zur eindeutigen Festlegung der Lage der Knotenlinie die Position eines der beiden Knoten. Vereinbarungsgemäß ist dies der aufsteigende Knoten.
Da die Erde sich dreht, ist das bekannte geographische Breiten-/Längengradsystem zur Positionsbestimmung ungeeignet. Stattdessen wird ein astronomisches Koordinatensystem verwendet, das als äquatoriales Koordinatensystem bekannt ist und sich nicht mit der Erde mitdreht. In diesem Koordinatensystem ist die Rektaszension
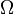 ein in der Äquatorebene gemessener Winkel zu einem fixen Referenzpunkt im Raum, für den
ein in der Äquatorebene gemessener Winkel zu einem fixen Referenzpunkt im Raum, für den 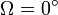 ist. Dieser Punkt heißt in der Astronomie Frühlingspunkt.
ist. Dieser Punkt heißt in der Astronomie Frühlingspunkt.Definition: Die Rektaszension
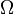 des aufsteigenden Knotens ist der vom Erdmittelpunkt aus gemessene Winkel zwischen Frühlingspunkt und aufsteigendem Knoten zum Zeitpunkt der Epoche. Vereinbarungsgemäß gilt:
des aufsteigenden Knotens ist der vom Erdmittelpunkt aus gemessene Winkel zwischen Frühlingspunkt und aufsteigendem Knoten zum Zeitpunkt der Epoche. Vereinbarungsgemäß gilt: 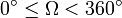 .
.Argument des Perigäums
Mit der Inklination und der Rektaszension des aufsteigenden Knotens ist die Lage der Bahnebene im Raum eindeutig definiert. Damit noch nicht beschrieben ist die Orientierung der elliptischen Umlaufbahn in der Bahnebene. Dies erfolgt durch einen weiteren Winkel, der als das Argument des Perigäums
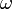 bekannt ist.
bekannt ist.Der Punkt, an dem der Satellit auf seiner elliptischen Bahn dem Erdmittelpunkt am nächsten ist, wird Perigäum genannt, der Punkt mit der größten Entfernung heißt Apogäum. Die Verbindungslinie zwischen diesen beiden Punkten ist die so genannte Apsidenlinie, die mit der Hauptachse der Bahnellipse identisch ist. Die Apsidenlinie führt ebenfalls wie die Knotenlinie durch den Erdmittelpunkt (Abb. 1).
Definition: Das Argument des Perigäums
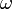 ist der vom Erdmittelpunkt aus gemessene Winkel zwischen aufsteigendem Knoten und Perigäum zum Zeitpunkt der Epoche. Vereinbarungsgemäß gilt:
ist der vom Erdmittelpunkt aus gemessene Winkel zwischen aufsteigendem Knoten und Perigäum zum Zeitpunkt der Epoche. Vereinbarungsgemäß gilt: 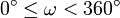 .
.Numerische Exzentrizität
Definition: Die numerische Exzentrizität
 gibt die Abweichung der elliptischen Umlaufbahn von der idealen Kreisform zum Zeitpunkt der Epoche an. Es gilt:
gibt die Abweichung der elliptischen Umlaufbahn von der idealen Kreisform zum Zeitpunkt der Epoche an. Es gilt: 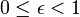 . Ist
. Ist 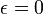 , ist die Ellipse ein Kreis.
, ist die Ellipse ein Kreis.Bei Satellitenbahnelementen wird immer die numerische Exzentrizität
 (meist ohne den Zusatz „numerisch“) angeben, nicht zu verwechseln mit der linearen Exzentrizität
(meist ohne den Zusatz „numerisch“) angeben, nicht zu verwechseln mit der linearen Exzentrizität  , die dem Abstand des Mittelpunktes der Ellipse zu den Brennpunkten entspricht. Da der Erdmittelpunkt immer in einem der beiden Brennpunkte der Bahnellipse liegt, gibt die lineare Exzentrizität
, die dem Abstand des Mittelpunktes der Ellipse zu den Brennpunkten entspricht. Da der Erdmittelpunkt immer in einem der beiden Brennpunkte der Bahnellipse liegt, gibt die lineare Exzentrizität  den Abstand Erdmitte – Ellipsenmitte an.
den Abstand Erdmitte – Ellipsenmitte an.Mittlere Bewegung
Das zweite Keplersche Gesetz stellt einen Zusammenhang zwischen der Geschwindigkeit und dem Abstand eines Satelliten vom Erdmittelpunkt her. Danach gilt: Satelliten auf einer kreisförmigen Umlaufbahn haben eine konstante Geschwindigkeit. Satelliten auf einer elliptischen Umlaufbahn haben im Perigäum ihre höchste und im Apogäum ihre geringste Geschwindigkeit. Für solche Bahnen wird in einem ersten Rechenschritt die über einen Umlauf gemittelte Geschwindigkeit betrachtet.
Definition: Aus der Durchschnittsgeschwindigkeit wird die mittlere Bewegung
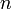 bestimmt und in den Satellitenbahnelementen in Umläufen pro Tag (d−1) angegeben.
bestimmt und in den Satellitenbahnelementen in Umläufen pro Tag (d−1) angegeben.Aus den Werten der mittleren Bewegung
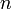 , der numerischen Exzentrizität
, der numerischen Exzentrizität  und der geozentrischen Gravitationskonstante
und der geozentrischen Gravitationskonstante 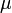 lassen sich die Zeit
lassen sich die Zeit 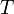 für einen Umlauf (Periode) und die Abmessungen der Bahnellipse berechnen:
für einen Umlauf (Periode) und die Abmessungen der Bahnellipse berechnen:-
-
Umlaufzeit 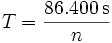
(1)
-
-
-
große Halbachse ![a=\sqrt[3]{\mu\cdot\frac{T^2}{4\pi^2}}](/pictures/dewiki/49/13efa329b2c3951dd06c1d671ca118da.png)
(2)
-
-
-
kleine Halbachse 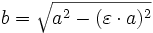
(3)
-
-
-
Abstand des Perigäums 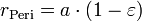
(4)
-
-
-
Abstand des Apogäums 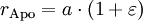
(5)
-
Mittlere Anomalie
Die mittlere Anomalie
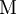 spezifiziert die Position des Satelliten auf seiner Bahn in Bezug auf das Perigäum.
spezifiziert die Position des Satelliten auf seiner Bahn in Bezug auf das Perigäum.Jeder Umlauf eines Satelliten beginnt vereinbarungsgemäß im Perigäum der elliptischen Umlaufbahn. Dabei überstreicht der Radiusvektor
 (Verbindungslinie Erdmittelpunkt – Satellit) während eines Umlaufs einen Winkel von 360°.
(Verbindungslinie Erdmittelpunkt – Satellit) während eines Umlaufs einen Winkel von 360°.Da sich nach dem zweiten Keplerschen Gesetz ein Satellit auf einer elliptischen Umlaufbahn nicht mit konstanter Geschwindigkeit bewegt, wird ähnlich wie bei der mittleren Bewegung zunächst von einem „gedachten“ Satelliten ausgegangen, der die Erde mit konstanter Geschwindigkeit auf einer Kreisbahn umläuft, deren Radius gleich der großen Halbachse
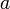 der tatsächlichen Bahnellipse ist (Abb. 2)
der tatsächlichen Bahnellipse ist (Abb. 2)Definition: Die mittlere Anomalie
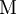 ist der vom Erdmittelpunkt aus gemessene Winkel zwischen dem Perigäum und der Position des gedachten Satelliten zum Zeitpunkt der Epoche. Vereinbarungsgemäß gilt:
ist der vom Erdmittelpunkt aus gemessene Winkel zwischen dem Perigäum und der Position des gedachten Satelliten zum Zeitpunkt der Epoche. Vereinbarungsgemäß gilt: 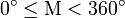 .
.Ist der Zeitpunkt
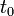 des Perigäumdurchgangs bekannt, kann die mittlere Anomalie
des Perigäumdurchgangs bekannt, kann die mittlere Anomalie 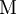 auch aus dem Zeitpunkt
auch aus dem Zeitpunkt 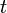 der Epoche und der Zeit
der Epoche und der Zeit 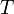 für einen Umlauf berechnet werden. Es gilt:
für einen Umlauf berechnet werden. Es gilt:-
-
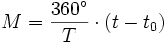 .
.(6)
-
Die tatsächliche Position, die wahre Anomalie
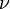 (Abb. 2) des Satelliten auf seiner elliptischen Umlaufbahn, wird über die exzentrische Anomalie
(Abb. 2) des Satelliten auf seiner elliptischen Umlaufbahn, wird über die exzentrische Anomalie 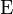 aus der berühmten Kepler-Gleichung bestimmt,
aus der berühmten Kepler-Gleichung bestimmt,-
-
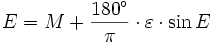 ,
,(7)
-
die als transzendente Gleichung nicht algebraisch, sondern nur durch numerische Verfahren gelöst werden kann (z. B. Newton-Raphson-Verfahren).
Hat man den Wert der exzentrischen Anomalie
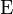 bestimmt, lässt sich die wahre Anomalie
bestimmt, lässt sich die wahre Anomalie 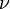 aus nachfolgender Beziehung ermitteln:
aus nachfolgender Beziehung ermitteln:-
-
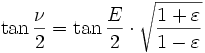 .
.(8)
-
Die Länge des Radiusvektors
 (Abstand des Satelliten vom Erdmittelpunkt) in Abhängigkeit von der wahren Anomalie lässt sich durch folgende Formel berechnen:
(Abstand des Satelliten vom Erdmittelpunkt) in Abhängigkeit von der wahren Anomalie lässt sich durch folgende Formel berechnen:-
-
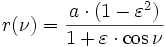 .
.(9)
-
Widerstandskoeffizient
Die oben bereits erwähnten Bremseffekte, die auf einen Satelliten einwirken, verursachen, dass dieser bei zunehmender Umlaufgeschwindigkeit in einer Spirale auf die Erde zurückstürzt und irgendwann in der Atmosphäre verglüht, wenn keine Gegenmaßnahmen (Bahnkorrektur-Manöver) ergriffen werden.
Abhängig vom verwendeten Propagationsmodell [2][3] gibt es verschiedene Ansätze:
Im einfachsten Fall, dem SGP-Modell (Simplified General Perturbations), ist der Widerstandskoeffizient entweder ein ballistischer Faktor oder die erste Ableitung der mittleren Bewegung nach der Zeit, geteilt durch zwei.
Definition 1: Der Widerstandskoeffizient ist ein Maß für die Sink-Rate pro Zeiteinheit, mit der der Satellit auf die Erde zustrebt. Ohne eigenes Formelzeichen wird er einfach
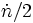 (sprich: n-Punkt Halbe) genannt und hat die Einheit Umläufe pro Tag im Quadrat (1/d2).
(sprich: n-Punkt Halbe) genannt und hat die Einheit Umläufe pro Tag im Quadrat (1/d2).Das 1966 für Satelliten im erdnahen Orbit entwickelte SGP-Modell basiert allerdings auf einer stark vereinfachten analytischen Störungstheorie und wird deshalb nur für angenäherte Berechnungen angewendet.
Am häufigsten wird für erdnahe Satelliten das 1970 entwickelte SGP4-Modell verwendet. Dessen Algorithmus wird auch von der NASA für alle Satelliten mit einer Umlaufzeit von unter 225 Minuten (entspricht einer Bahnhöhe bis etwa 6.000 km) benutzt.
Definition 2: Der Widerstandskoeffizient im SGP4-Modell wird
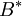 (sprich: B-Stern oder engl. B-Star) genannt und ist wie folgt spezifiziert:
(sprich: B-Stern oder engl. B-Star) genannt und ist wie folgt spezifiziert:In der aerodynamischen Theorie hat jedes Objekt einen ballistischen Koeffizienten
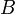 , der sich aus seiner Masse
, der sich aus seiner Masse 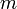 geteilt durch das Produkt seines (Luft-)Widerstandsbeiwertes
geteilt durch das Produkt seines (Luft-)Widerstandsbeiwertes 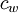 (meist ein Wert zwischen 2 und 4) und seiner Querschnittsfläche
(meist ein Wert zwischen 2 und 4) und seiner Querschnittsfläche 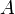 berechnet (s. a. Lebensdauer von Satellitenorbits):
berechnet (s. a. Lebensdauer von Satellitenorbits):-
-
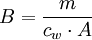
(10)
-
Der ballistische Koeffizient sagt aus, wie stark ein Objekt abgebremst wird: Je höher der Wert umso niedriger die Bremswirkung. (HINWEIS: In der Veröffentlichung „Models for Propagation of NORAD Element Sets“[2] wird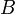 anders definiert, siehe dort Kapitel 12.)
anders definiert, siehe dort Kapitel 12.)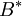 ist ein erweiterter Wert von
ist ein erweiterter Wert von 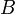 und verwendet als Referenzwert die Dichte
und verwendet als Referenzwert die Dichte 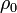 der Atmosphäre bei der Referenzhöhe
der Atmosphäre bei der Referenzhöhe 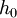 .
. 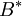 hat die Einheit Erdradien−1.
hat die Einheit Erdradien−1.-
-
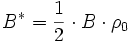
(11)
-
In
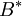 fließen die Luftdichte der Atmosphäre und der Widerstandsbeiwert des Satelliten mit ein. Diese sind bedingt durch die wechselnde Sonnenaktivität und die daraus resultierende wechselnde Zusammensetzung der Atmosphäre stark variabel. Die sinnvolle Nutzungsdauer von SGP4 wird dadurch für LEO-Satelliten auf wenige Tage bis einzelne Wochen beschränkt, da
fließen die Luftdichte der Atmosphäre und der Widerstandsbeiwert des Satelliten mit ein. Diese sind bedingt durch die wechselnde Sonnenaktivität und die daraus resultierende wechselnde Zusammensetzung der Atmosphäre stark variabel. Die sinnvolle Nutzungsdauer von SGP4 wird dadurch für LEO-Satelliten auf wenige Tage bis einzelne Wochen beschränkt, da 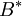 exakt nur für die Atmosphäre zur Epoche gilt.
exakt nur für die Atmosphäre zur Epoche gilt.Das Two Line Elements Format TLE
Satellitenbahnelemente können in ein Format kodiert werden, das allgemein als das NASA/NORAD Two Line Elements Format, kurz TLE, bekannt ist.[4] Wie der – allgemein übliche – englische Ausdruck schon sagt, werden die Elemente als Ziffernblöcke in zwei Zeilen dargestellt. Die Darstellung ist historisch begründet, da diese ursprünglich für 80-Spalten-Lochkarten entwickelt und mit FORTRAN-Programmen weiterverarbeitet wurde. Die Parameter der Umlaufbahn und die Satelliten-Position können dann mit einem der Propagations-Modelle[2][3] für einen gewünschten Zeitpunkt vorausberechnet werden. Aus Gründen der Genauigkeit sollten die Bahnelemente insbesondere für Satelliten mit niedrigem Orbit nicht älter als wenige Tage sein. Ohne den großen Aufwand der zum Teil sehr komplexen numerischen Verfahren lassen sich Lage und Form der Umlaufbahn sowie die Position des Satelliten zumindest zum Zeitpunkt der Epoche berechnen, wie das Beispiel in Abschnitt 2.2 zeigt.
Anwendung
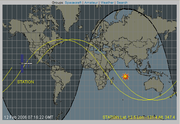 Abbildung 3: Groundtrack (Bodenpfad) der Internationalen Raumstation [5]
Abbildung 3: Groundtrack (Bodenpfad) der Internationalen Raumstation [5]Mit so genannten Tracking-Programmen[1] lässt sich ein Satellit in Echtzeit verfolgen (Abb. 3) oder der Zeitpunkt des Überflugs über einen bestimmten Punkt auf der Erde berechnen. Denn unter bestimmten Voraussetzungen kann man die Überflüge von der Erde aus selbst mit bloßem Auge beobachten. Das gilt besonders – wegen ihrer Größe – für die Internationale Raumstation.
Beispiel
Two Line Elements der Internationalen Raumstation ISS
Epoche: 9. Feb. 2006, 20:26:00,0 h UTC ( = MEZ – 1 h)
NORAD-Originalformat (zwei Zeilen, 69 Zeichen pro Zeile inklusive Leerstellen):
ISS(ZARYA) 1 25544U 98067A 06040.85138889 .00012260 00000-0 86027-4 0 3194 2 25544 51.6448 122.3522 0008835 257.3473 251.7436 15.74622749413094
Aufbereitetes Format: Zum besseren Verständnis sind fehlende Leerzeichen, Exponenten, anführende Nullen und Dezimalpunkte ergänzt (Änderungen rot markiert). Außerdem ersetzen Kommata die Dezimalpunkte. So aufbereitet können die Elemente z. B. von Microsoft Excel weiterverwendet werden.
1 25544_U 98067A 2006_040,85138889 0,00012260 0,0000e-0 0,86027e-4 0 319_4 2 25544 51,6448 122,3522 0,0008835 257,3473 251,7436 15,74622749_41309_4
Erläuterung der Zahlengruppen
Im Folgenden sind die Zahlengruppen anhand des aufbereiteten Formats erklärt:
1. Zeile:
-
-
1 Zeile Nr. 1 25544 NORAD-Katalog-Nr. U Klassifizierung (U=unklassifiziert) 98067A Internationale Bezeichnung, d.h. Startjahr (2 Ziffern), Startnummer im Jahr (3 Ziffern), Objekt des Starts (max. 3 Zeichen) 2006 Epoche: Jahr 2006 040,85138889 Epoche: Tag-Nr. 40 = 9. Februar, Tages-Bruchteil 0,8516889 = 20h 26min 00,0s 0,00012260 Widerstandskoeffizient im SGP-Modell: 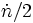 = 0,00012260 d−2
= 0,00012260 d−20,0000e-0 vernachlässigbarer Widerstandskoeffizient im SGP-Modell (meist Null): 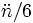 = 0·10−0 d−3
= 0·10−0 d−30,86027e-4 Widerstandskoeffizient im SGP4-Modell: B * = 8,6027·10−5 Erdradien−1 0 Ephemeridentyp (0 = SGP4-Modell) 319 laufende Datensatz-Nummer 4 Prüfsumme Modulo 10
-
2. Zeile:
-
-
2 Zeile Nr. 2 25544 NORAD-Katalog-Nr. 51,6448 Inklination i = 51,6448° 122,3522 Rektaszension des aufsteigenden Knotens Ω = 122,3522° 0,0008835 numerische Exzentrizität der Umlaufbahn ε = 0,0008835 257,3473 Argument des Perigäums ω = 257,3473° 251,7436 Mittlere Anomalie Μ = 251,7436° 15,74622749 Mittlere Bewegung: n = 15,74622749 d−1 41309 Umlauf Nr. 41309 seit dem Start 4 Prüfsumme Modulo 10
-
Erläuterung zur Darstellung der Epoche
Die Darstellung des Datums und der Uhrzeit im gewohnten Format (Jahr-Monat-Tag) sowie (Stunden:Minuten:Sekunden) ist für Berechnungsprogramme zu unhandlich. Deshalb wird für Satellitenbahnelemente anstatt des gewohnten Formats ein Dezimalformat verwendet.
In oben stehendem Beispiel ist im TLE-Format der Zeitpunkt der Epoche durch die Ziffernfolge 06040.85138889 dargestellt.
In der 5-stelligen Zifferngruppe vor dem Dezimalpunkt stehen die beiden ersten Ziffern 06 für das Jahr der Epoche, hier also 2006.
Die nächsten drei Ziffern 040 stehen für die laufende Tag-Nummer im Jahr. Für den 1. Januar stehen die Ziffern 001, für den 31. Dezember stehen die Ziffern 365 (in einem Schaltjahr 366). Demnach stehen die Ziffern 040 für den 9. Februar.
Die 8-stellige Zifferngruppe nach dem Dezimalpunkt steht für den Bruchteil eines Tages, hier also das 0,85138889-fache eines Tages. Das wiederum lässt sich in eine Uhrzeit umrechnen und ergibt hier 20h 26min 00,0s koordinierte Weltzeit UTC:
-
-
- 0,85138889 Tage · 86 400 Sekunden/Tag = 73 560 Sekunden = 20h 26min 0,0 s
-
Berechnungsbeispiel
Umlaufbahn und Position
Eingesetzt in die Gleichungen (1)–(9), ergeben sich für die Lage und Orientierung der Umlaufbahn, die Position und die Widerstandskoeffizienten der Internationalen Raumstation ISS aus den NORAD Two Line Elements zum Zeitpunkt der Epoche folgende Werte:
-
-
Epoche: t = 9. Februar 2006; 20:26:00,0h UTC Inklination: i = 51,6448° Rektaszension des aufsteigenden Knotens: Ω = 122,3522° Argument des Perigäums: ω = 257,3773° mittlere Bewegung: n = 15, 74622749 d−1 Umlaufzeit: T = 5.487,029 s große Halbachse: a = 6.723.842,235 m numerische Exzentrizität: ε = 0,0008835 kleine Halbachse: b = 6.723.839,610 m Abstand des Perigäums v. Erdmittelpunkt: rPeri = 6.717.901,720 m Abstand des Apogäums v. Erdmittelpunkt: rApo = 6.729.872,750 m mittlere Anomalie: Μ = 251,7436° exzentrische Anomalie: Ε = 251,6955° wahre Anomalie: ν = 251,6475° Radiusvektor: r(ν) = 6.725.707,950 m Widerstandskoeffizient im SGP-Modell: 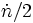 = 0,00012260 d−2
= 0,00012260 d−2Widerstandskoeffizient im SGP4-Modell: 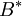 = 8,6027·10−5 Erdradien−1
= 8,6027·10−5 Erdradien−1
-
Die oben aufgeführten Zahlenwerte können nun in einem der Propagations-Modelle [2][3] für Vorhersage-Berechnungen verwendet werden. Wegen der erdnahen Umlaufbahn der Internationalen Raumstation kommt entweder das SGP- oder das SGP4-Modell in Frage, die sich hauptsächlich durch die verwendeten Störungstheorien und damit den Rechenaufwand unterscheiden. Präzise Vorhersagen lassen sich nur mit dem SGP4-Modell machen.
Anmerkungungen zu den Ergebnissen:
- Zur Berechnung der großen Halbachse
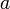 mit Gleichung (2) wurde für das Produkt aus Gravitationskonstante
mit Gleichung (2) wurde für das Produkt aus Gravitationskonstante 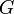 und Masse der Erde
und Masse der Erde 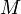 (
(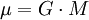 ) der Wert aus dem European Vertical Reference System übernommen [6] :
) der Wert aus dem European Vertical Reference System übernommen [6] : 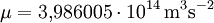 .
.
- Man sieht, dass die Umlaufbahn durch den kleinen Wert der numerischen Exzentrizität
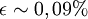 nur um
nur um 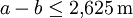 vom Radius der idealen Kreisbahn abweicht. Für Näherungsrechnungen kann deshalb in einem solchen Fall von einer Kreisbahn mit Radius
vom Radius der idealen Kreisbahn abweicht. Für Näherungsrechnungen kann deshalb in einem solchen Fall von einer Kreisbahn mit Radius  ausgegangen werden.
ausgegangen werden.
- In vielen Tracking-Programmen wird anstatt des Abstandes vom Erdmittelpunkt jeweils die Höhe über der Erdoberfläche im Perigäum, Apogäum oder der aktuellen Position ermittelt, wobei nicht immer ganz klar ist, welche Referenz die Programme zur Berechnung benutzen. Meist ist dies der Erdradius am Äquator. Da die Erde keine Kugel, sondern ein Ellipsoid ist (siehe WGS84), stimmt das aber nur, wenn die entsprechenden Punkte genau über dem Äquator liegen. Genau genommen müsste man für die entsprechende Satellitenposition den Fußpunkt (Nadir) auf der Erdoberfläche bestimmen und von dort aus die momentane, tatsächliche Höhe über Grund berechnen. Manche Programme verwenden zur Bahnhöhenbestimmung auch einen mittleren Radius des Rotationsellipsoids der Erde.
- Aus der Kepler-Gleichung ist mit Hilfe des Newton-Raphson-Verfahrens zur iterativen Berechnung von Nullstellen die exzentrische Anomalie
 bestimmt worden und aus ihr schließlich die wahre Anomalie
bestimmt worden und aus ihr schließlich die wahre Anomalie  . Da die Umlaufbahn fast einer Kreisbahn entspricht, beträgt die Differenz zwischen mittlerer und wahrer Anomalie gerade einmal 0,096°. Auch hier gilt: Ist die numerische Exzentrizität
. Da die Umlaufbahn fast einer Kreisbahn entspricht, beträgt die Differenz zwischen mittlerer und wahrer Anomalie gerade einmal 0,096°. Auch hier gilt: Ist die numerische Exzentrizität  sehr klein, kann für Näherungsrechnungen die wahre Anomalie
sehr klein, kann für Näherungsrechnungen die wahre Anomalie  gleich der mittleren Anomalie
gleich der mittleren Anomalie 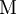 gesetzt werden.
gesetzt werden.
Auswirkungen der Bahnstörungen
Für einfache Berechnungen genügt es, lediglich die Bahnstörungen durch die abgeplattete Form der Erde und den Bremseffekt durch die hohe Atmosphäre zu berücksichtigen.
Gravitationseinflüsse
Auf die Bahnebene der Umlaufbahn eines erdnahen Satelliten übt das unregelmäßige Gravitationsfeld der Erde ein „Kippmoment“ aus, dem die Bahnebene durch eine Präzessionsbewegung nach den Kreiselgesetzen ausweicht. Diese Ausweichbewegung führt dazu, dass der aufsteigende Knoten bzw. die Knotenlinie nicht feststeht, sondern langsam in der Äquatorebene rotiert und sich damit die Rektaszension des aufsteigenden Knotens
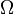 ständig ändert. Die Bahnebene dreht sich quasi um die z-Achse des astronomischen Koordinatensystems (Abb. 1). Diese zeitliche Änderung in Grad pro Tag (°/d) kann mit folgender Beziehung berechnet werden (rA = Erdradius):
ständig ändert. Die Bahnebene dreht sich quasi um die z-Achse des astronomischen Koordinatensystems (Abb. 1). Diese zeitliche Änderung in Grad pro Tag (°/d) kann mit folgender Beziehung berechnet werden (rA = Erdradius):-
-
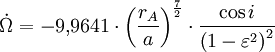 .
.(12)
-
Gleichzeitig dreht sich die Apsidenlinie in der Bahnebene – ebenfalls durch Schwerkrafteinflüsse – um den Erdmittelpunkt. Damit erfährt auch das Argument des Perigäums
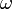 eine zeitliche Änderung, die in Grad pro Tag (°/d) berechnet werden kann:
eine zeitliche Änderung, die in Grad pro Tag (°/d) berechnet werden kann:-
-
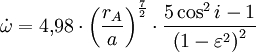 .
.(13)
-
Setzt man in beide Gleichungen die entsprechenden Werte aus dem TLE-Beispiel ein, ergibt sich, dass die Rektaszension des aufsteigenden Knotens um 5,1401°/d abnimmt und das Argument des Perigäums um 3,8308°/d zunimmt. Bei dieser Rechnung wird allerdings unterstellt, dass die Werte der großen Halbachse
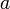 , der Inklination
, der Inklination 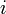 und der numerischen Exzentrizität
und der numerischen Exzentrizität  konstant bleiben, was in der Realität aber nicht der Fall ist (siehe Abschnitt 4: Änderungen über einen längeren Zeitraum). Für eine sehr kurzfristige Vorhersageberechung ist dies trotzdem hinreichend genau.
konstant bleiben, was in der Realität aber nicht der Fall ist (siehe Abschnitt 4: Änderungen über einen längeren Zeitraum). Für eine sehr kurzfristige Vorhersageberechung ist dies trotzdem hinreichend genau.Bremswirkung
Im einfachsten Fall ist der Widerstandskoeffizient die erste Ableitung der mittleren Bewegung nach der Zeit und in den TLE des obigen Beispiels für die ISS mit
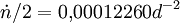 , also
, also 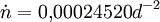 gegeben.
gegeben.Basierend auf der mittleren Bewegung aus den TLE erhöht sich damit jeden Tag die Anzahl der Umläufe pro Tag auf
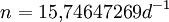 . Eingesetzt in die Gleichungen (1) und (2) ergibt das eine Abnahme der großen Halbachse
. Eingesetzt in die Gleichungen (1) und (2) ergibt das eine Abnahme der großen Halbachse  um 67,177 Meter pro Tag.
um 67,177 Meter pro Tag.Diagramme
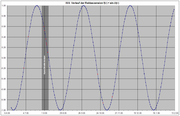
Wie sich die Satellitenbahnelemente tatsächlich im Lauf der Zeit ändern, zeigt eine Aufzeichnung über einen längeren Zeitraum. Im Folgenden ist für die Internationale Raumstation ISS der Verlauf der Two Line Elements (244 Datensätze) und der daraus abgeleiteten Größen für den Zeitraum vom 11. Juni 2005 bis 11. Februar 2006 graphisch aufbereitet. In den Diagrammen stellt die x-Achse jeweils die Zeitachse, die y-Achse die zugehörigen Werte dar. Im dunkel markierten Zeitraum (27. Juli – 6. August 2006) war das Space Shuttle Discovery während der STS-114-Mission angedockt.
Verlauf der mittleren Bewegung
Die mittlere Bewegung
 ist das Satellitenbahnelement, bei dem die Änderung durch den Bremseffekt mit am auffälligsten ist. Je näher ein Satellit der Erde kommt, desto höher wird seine Umlaufgeschwindigkeit und damit die Anzahl der Umläufe pro Tag (Diagramm 1).
ist das Satellitenbahnelement, bei dem die Änderung durch den Bremseffekt mit am auffälligsten ist. Je näher ein Satellit der Erde kommt, desto höher wird seine Umlaufgeschwindigkeit und damit die Anzahl der Umläufe pro Tag (Diagramm 1).Damit die ISS nicht irgendwann in der Atmosphäre verglüht, wird die Umlaufbahn von Zeit zu Zeit angehoben. Diese „Orbit-Reboost“ genannten Bahnkorrekturmanöver erfolgen durch Zündung der bordeigenen oder der Triebwerke des angedockten Space Shuttles oder Progress-Raumschiffes. Die roten Punkte in den nebenstehenden Diagrammen markieren jeweils den Zeitpunkt eines Reboost. Je nach Brenndauer der Triebwerke, wird die Bahn mehr oder weniger stark angehoben und damit die Anzahl der Umläufe wieder reduziert. Weitere Auswirkungen sind in den folgenden Abschnitten erklärt.
Verlauf der großen Halbachse
Die Änderung der großen Halbachse
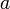 ist umgekehrt proportional zur Änderung der mittleren Bewegung
ist umgekehrt proportional zur Änderung der mittleren Bewegung 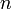 (siehe Gleichungen (1) und (2)). An ihr ist das Absinken und Anheben der Umlaufbahn am besten nachvollziehbar (Diagramm 2).
(siehe Gleichungen (1) und (2)). An ihr ist das Absinken und Anheben der Umlaufbahn am besten nachvollziehbar (Diagramm 2).Man sieht, dass während der STS-114-Mission durch Zündung der Shuttle-Triebwerke die Umlaufbahn insgesamt sechsmal korrigiert wurde. Neben weiteren kleineren erfolgte eine signifikante Änderung am 11. November 2005, als die große Halbachse um 7.731,5 m zunahm.
Man sieht auch, dass die Abnahme nicht gleichmäßig erfolgt. Ursache hierfür sind Änderungen in der Dichte der „hohen“ Atmosphäre, die durch die unregelmäßige Aktivität der Sonne verursacht werden. Um eine längerfristige Tendenz zu ermitteln, kann man trotzdem einen linearen Trend berechnen. Im Diagramm ist dies ab dem letzten Orbit-Reboost dargestellt. Die Steigung bzw. Sinkrate der Regressionsgeraden (y = m·x + b) beträgt im Durchschnitt −81,7 Meter pro Tag.
Verlauf der Inklination
Die Neigung der Bahnebene schwankt leicht um einen Mittelwert von
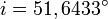 . Ursache hierfür sind in erster Linie Gravitationseinflüsse des Mondes. Signifikante Sprünge resultieren meist aus den Bahnkorrekturmanövern (Diagramm 3).
. Ursache hierfür sind in erster Linie Gravitationseinflüsse des Mondes. Signifikante Sprünge resultieren meist aus den Bahnkorrekturmanövern (Diagramm 3).Verlauf der numerischen Exzentrizität
Die numerische Exzentrizität
 wird vor allem durch den Strahlungsdruck der Sonne und durch die Sonnenwinde beeinflusst, die eine Beschleunigung von der Sonne weg verursachen. Abhängig ist dies neben der Sonnenaktivität auch vom Reflexionsfaktor und von der Größe der Solar-Panels eines Satelliten, die bei der ISS mit 74 Meter Breite (Ausbaustufe 2005) relativ groß sind.
wird vor allem durch den Strahlungsdruck der Sonne und durch die Sonnenwinde beeinflusst, die eine Beschleunigung von der Sonne weg verursachen. Abhängig ist dies neben der Sonnenaktivität auch vom Reflexionsfaktor und von der Größe der Solar-Panels eines Satelliten, die bei der ISS mit 74 Meter Breite (Ausbaustufe 2005) relativ groß sind.Obwohl die Werte der numerischen Exzentrizität sehr klein sind – Abweichung von der idealen Kreisbahn zwischen 0,0685 ‰ und 1,1033 ‰ – ist bei entsprechender Skalierung ein deutlicher Sprung zum Zeitpunkt des letzten Orbit-Reboost zu sehen (Diagramm 4). Das liegt daran, dass die Beschleunigung beim Anheben der Umlaufbahn hauptsächlich in Richtung des Apogäums gewirkt hat und die Bahnellipse dadurch etwas gestreckt wurde, was wiederum eine Zunahme der Exzentrizität mit sich bringt (siehe auch nächster Abschnitt Bahnhöhen-Diagramm). Sind solche Bahnkorrektur-Manöver geplant, gibt das die NASA in ihren Bulletins bekannt [7], denen man die Richtungs- und Geschwindigkeitsänderung in Vektordarstellung entnehmen kann (Achtung: Die Angaben dort erfolgen in feet per seconds und nautical miles).
Verlauf der Bahnhöhen
In den meisten Tracking-Programmen wird für das Perigäum und Apogäum anstatt des Abstandes vom Erdmittelpunkt die Höhe in Kilometer über der Erdoberfläche angegeben. Häufig fehlt aber eine Angabe zum verwendeten Radius der Erde. Referenz hier ist der Äquatorradius des WGS84-Ellipsoids mit 6.378,137 km. Dieser Wert wird von den aus den Gleichungen (4) und (5) gewonnenen Resultaten subtrahiert, und man erhält die Bahnhöhen im Perigäum und Apogäum über der Erde.
Erst hier zeigt sich der tatsächliche Bahnverlauf, da die Schwankungen der numerischen Exzentrizität
 direkt einfließen. Deshalb ist in Diagramm 5 zusätzlich noch einmal der Verlauf der numerischen Exzentrizität
direkt einfließen. Deshalb ist in Diagramm 5 zusätzlich noch einmal der Verlauf der numerischen Exzentrizität  dargestellt, um den Einfluss deutlich zu machen.
dargestellt, um den Einfluss deutlich zu machen.Weiterhin wird hier der im vorhergehenden Abschnitt angesprochene Effekt deutlich, nämlich dass sich der letzte Orbit-Reboost mehr in Richtung des Apogäums ausgewirkt hat. Die Bahnhöhenzunahme im Apogäum beträgt 12,172 km im Gegensatz zu 3,292 km im Perigäum.
Verlauf der Rektaszension des aufsteigenden Knotens
Nach den Kreiselgesetzen rotiert der aufsteigende Knoten um die z-Achse des astronomischen Koordinatensystems (siehe Abschnitt 3.2.1). Dargestellt als Funktion des Sinus (Diagramm 6a), ergibt sich für die Rektaszension des aufsteigenden Knotens
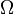 ein fast harmonischer Verlauf, d. h. die zeitliche Änderung ist fast linear.
ein fast harmonischer Verlauf, d. h. die zeitliche Änderung ist fast linear.Erst wenn man die Werte der mittleren Rotation pro Tag bestimmt (Diagramm 6b), sieht man diese leicht von einem Mittelwert abweichen. Außerdem lässt sich eine Tendenz erkennen, dass zwischen zwei Orbit Reboost – der zeitliche Abstand muss nur groß genug sein – die Rotationsrate um etwa 0,00025° pro Tag zunimmt. Nach Gleichung (12) muss das auch so sein, da dort die große Halbachse
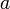 mit der Zeit als abnehmende Größe eingeht. Die kleinen Schwankungen der Rotation um die Regressionsgerade resultieren aus den Schwankungen der Inklination
mit der Zeit als abnehmende Größe eingeht. Die kleinen Schwankungen der Rotation um die Regressionsgerade resultieren aus den Schwankungen der Inklination 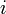 und der numerischen Exzentrizität
und der numerischen Exzentrizität  .
.Verlauf des Arguments des Perigäums
Die Rotation der Apsidenlinie und damit des Perigäums erfolgt alles andere als stabil. Vergleicht man den Verlauf in Diagramm 7 mit dem der numerischen Exzentrizität
 in Diagramm 4 fällt auf, dass erst mit einer deutlichen Zunahme der Exzentrizität die Rotation harmonischer verläuft.
in Diagramm 4 fällt auf, dass erst mit einer deutlichen Zunahme der Exzentrizität die Rotation harmonischer verläuft.Berechnet man für diesen Bereich (ab dem 11. November 2005) mit einer Regressionsanalyse die durchschnittliche Änderung, so nimmt das Argument des Perigäums um 3,7669° pro Tag zu.
Quellen
- ↑ a b Trackingprogramme und TLE-Quellen (englisch)
- ↑ a b c d e Models for Propagation of NORAD Element Sets (pdf-Datei, englisch)
- ↑ a b c d Sebastian Stabroth, Institut für Luft- und Raumfahrtsysteme, TU Braunschweig, Der NASA-TLE-Objektkatalog (pdf-Datei)
- ↑ NASA: NASA/NORAD 2-Line Elements (englisch)
- ↑ Science@NASA: Satellite Tracking (englisch)
- ↑ European Vertical Reference System (englisch)
- ↑ NASA Human Space Flight: Real Time Data, ISS Trajectory Data (englisch)
Siehe auch
- Bahnbestimmung
- Störungsrechnung
- Satellite Catalog Number
- Astronomische Bezeichnung von Raumflugkörpern
-
Wikimedia Foundation.