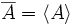Ergodik

Die Ergodenhypothese der statistischen Mechanik besagt, dass ein zeitlicher Mittelwert gleich dem Ensemble- oder Scharmittelwert ist. Ergodisch ist ein dynamisches System nur dann, wenn die Trajektorie jedem Punkt im Phasenraum (der mit den äußeren Zwängen vereinbar ist) in endlicher Zeit beliebig nahe kommt. Es gilt dann:

$\overline{A}=\langle A\rangle$

Genau genommen ist die Ergodenhypothese der statistischen Mechanik die Hypothese, dass die Trajektorie jeden Punkt im Phasenraum (der mit den äußeren Zwängen vereinbar ist) durchläuft. Dies ist die ursprüngliche Formulierung von Ludwig Boltzmann aus dem Jahr 1887.^[1] Die am Anfang erläuterte Form der Ergodenhypothese heißt Quasi-Ergodenhypothese: Weil die Trajektorie jedem Punkt im Phasenraum (der mit den äußeren Zwängen vereinbar ist) in endlicher Zeit zwar beliebig nahe kommt, ihn aber nicht immer durchläuft, ist die ursprüngliche Ergodenhypothese mathematisch nicht haltbar.

Die Ergodenhypothese wird häufig auch als Ergodentheorem bezeichnet (wobei meist das Quasi-Ergodentheorem gemeint ist). Wichtig ist sie als Grundlage der statistischen Mechanik, als Hypothese vom molekularem Chaos. Obwohl sie anschaulich einfach erscheint, ist ihre strenge mathematische Rechtfertigung besonders schwierig.^[2]

Man verwendet diesen Begriff auch in der Systemtheorie zur Klassifizierung von Systemen bzw. der von ihnen erzeugten Signale. Ein ergodisches Signal ist ein stochastisches (dem Zufall unterworfenes) stationäres Signal, das sowohl aperiodisch als auch wiederkehrend ist. Dies ist z. B. der Fall, wenn das Signal eine markante Wellenform hat, ohne dass sich diese in festen Intervallen wiederholt. Ergodische Systeme tendieren dazu, ein Ausgangssignal zu erzeugen, das von der Initialanregung nur wenig abhängig ist.

Im Fall spontaner Symmetriebrechung wird die Ergodenhypothese verletzt (Ergodizitätsbrechung). Es gibt dann disjunkte ergodische Bereiche im Phasenraum. Dies kann bei Phasenübergängen geschehen, etwa beim Erstarren einer Flüssigkeit oder bei Spingläsern.

Einzelnachweise

1. ↑ Richard Becker, Theorie der Wärme, 1. Aufl., Springer-Verlag, S. 97
2. ↑ Albert Messiah, Quantenmechanik, Band 1, 2. Aufl., S. 17

Weblinks

• Ergodizität in Markow-Ketten