- Ergodentheorie
-
Ergodizität ist ein Begriff innerhalb des mathematischen Teilgebiets der Stochastik. Die Statistik eines Prozesses wird von einer Musterfunktion beschrieben.
Inhaltsverzeichnis
Vorbereitungen
Man nennt zu einem Wahrscheinlichkeitsraum
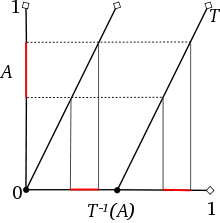
 eine messbare Abbildung T maßerhaltend, falls das Bildmaß von P unter T wieder P ist, d. h. P(T − 1(A)) = P(A) für alle Mengen A aus der σ-Algebra
eine messbare Abbildung T maßerhaltend, falls das Bildmaß von P unter T wieder P ist, d. h. P(T − 1(A)) = P(A) für alle Mengen A aus der σ-Algebra  . Weiterhin heißt eine Menge A T-invariant, falls T − 1(A) = A.
. Weiterhin heißt eine Menge A T-invariant, falls T − 1(A) = A.Definition
Eine maßerhaltende Transformation heißt nun ergodisch, falls für alle T-invarianten Mengen A gilt, dass
 .
.Anwendungen
Mathematisch gesehen stellt der Birkhoffsche Ergodensatz für ergodische Maßtransformationen eine Variante des Starken Gesetzes der großen Zahlen dar. Dabei können durchaus auch abhängige Zufallsvariablen betrachtet werden.
Ergodizität in der Zeitreihenanalyse
Für die statistische Inferenz mit Zeitreihen müssen Annahmen getroffen werden, da in der Praxis meist nur eine Realisation des die Zeitreihe generierenden Prozesses vorliegt. Die Annahme der Ergodizität bedeutet, dass Stichprobenmomente, die aus einer endlichen Zeitreihe gewonnen werden für
 quasi gegen die Momente der Grundgesamtheit konvergieren. Für
quasi gegen die Momente der Grundgesamtheit konvergieren. Für ![\operatorname{E}[x_t]=\mu](d/d4dccbfaa0521f96c96a3017f9593312.png) und
und ![\operatorname{V}[x_t]](d/9edf0370b4a8c9666ac11136c464c545.png) konstant:
konstant:
mittelwertergodisch:![\lim_{T \rightarrow \infty}\operatorname{E}\left[\left(\frac{1}{T}\sum_{t=1}^{T}x_t-\mu\right)^2\right] = 0](d/3bd8b230c765ea30d9d23d6afeef54f0.png)
varianzergodisch:
![\lim_{T \rightarrow \infty}\operatorname{E}\left[\left(\frac{1}{T}\sum_{t=1}^{T}(x_t-\mu)^2-\sigma^2\right)^2\right] = 0](f/a4f7df1738e75f79122d56d77452d5b1.png)
Diese Eigenschaften bei abhängigen Zufallsvariablen lassen sich nicht empirisch nachweisen und müssen daher unterstellt werden. Damit ein stochastischer Prozess ergodisch sein kann, muss er sich in einem statistischem Gleichgewicht befinden, d.h. er muss stationär sein.Ergodizität in der Ergodenhypothese
Ein statistisches System wählt aus einem definierten Zahlenraum Zufallszahlen aus. Das System erreicht dabei den ganzen verfügbaren Zahlenraum und die Wahrscheinlichkeit jeder Zahl aufzutreten ist gleich groß.
Siehe auch
Literatur
Historisch
- G. D. Birkhoff, Proof of the ergodic theorem, (1931), Proc Natl Acad Sci U S A, 17 pp 656-660.
- J. von Neumann, Proof of the Quasi-ergodic Hypothesis, (1932), Proc Natl Acad Sci U S A, 18 pp 70-82.
- J. von Neumann, Physical Applications of the Ergodic Hypothesis, (1932), Proc Natl Acad Sci U S A, 18 pp 263-266.
- E. Hopf, Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krümmung, (1939) Leipzig Ber. Verhandl. Sächs. Akad. Wiss. 91, p.261-304.
- S. V. Fomin and I. M. Gelfand, Geodesic flows on manifolds of constant negative curvature, (1952) Uspehi Mat. Nauk 7 no. 1. p. 118-137.
- F. I. Mautner, Geodesic flows on symmetric Riemann spaces, (1957) Ann. of Math. 65 p. 416-431.
- C. C. Moore, Ergodicity of flows on homogeneous spaces, (1966) Amer. J. Math. 88, p.154-178.
Modern
- D.V. Anosov: Ergodic theory, metric theory of dynamical systems, Springer
- Wladimir Igorewitsch Arnold and André Avez, Ergodic Problems of Classical Mechanics. New York: W.A. Benjamin. 1968.
- Leo Breiman, Probability. Original edition published by Addison-Wesley, 1968; reprinted by Society for Industrial and Applied Mathematics, 1992. ISBN 0-89871-296-3. (See Chapter 6.)
- Peter Walters, An introduction to ergodic theory, Springer, New York, 1982, ISBN 0-387-95152-0.
- Tim Bedford, Michael Keane, Caroline Series (Hrsg.): Ergodic theory, symbolic dynamics and hyperbolic spaces. Oxford University Press, 1991, ISBN 0-19-853390-X. (A survey of topics in ergodic theory; with exercises.)
- Joseph M. Rosenblatt and Máté Weirdl, Pointwise ergodic theorems via harmonic analysis, (1993) appearing in Ergodic Theory and its Connections with Harmonic Analysis, Proceedings of the 1993 Alexandria Conference, (1995) Karl E. Petersen and Ibrahim A. Salama, eds., Cambridge University Press, Cambridge, ISBN 0-521-45999-0. (An extensive survey of the ergodic properties of generalizations of the equidistribution theorem of shift maps on the unit interval. Focuses on methods developed by Bourgain.)
Wikimedia Foundation.


 .
.