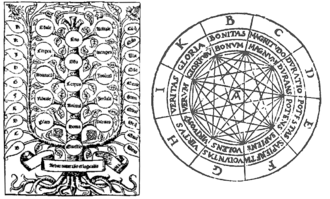
Ars generalis ultima

Arbor naturalis et logicalis, Natürlicher logischer Baum.
Der Mittelteil des Baumes entspricht der Arbor porphyrii, die zusätzlichen Blätter auf der rechten Seite stehen für zehn Arten von Fragen, die Blätter links sind Buchstabenschlüssel.
Daneben Ars Magna Figura 1

Die Ars generalis ultima ist ein um etwa 1305 ⁽¹⁾ abgeschlossenes, erstmals nach 1500 gedrucktes Werk, in dem der mallorquiner Philosoph, Logiker und Theologe Ramon Llull die Ars magna, die Große Kunst erläutert, durch mechanisches Kombinieren von Begriffen mittels einer von ihm erdachten „logischen Maschine“ zu Erkenntnissen zu gelangen. Angenommen werden darf, dass er zu seinen Rechenscheiben durch Instrumente arabischer Astronomen und Astrologen, aber auch durch Anschauungen der Kabbalistik inspiriert war.

Eine Baumstruktur, die stark auf die Arbor porphyriana zurückgreift, erweitert Llull durch Schlüsselfragen zu den 45 in der Tafel der Prinzipien zusammengefassten Grundtermini. Beziehungen zwischen diesen Prinzipien werden nicht willkürlich hergestellt, sondern anhand eines logischen Apparats, der durch vier „Figuren“, drei Kreisscheiben und eine Permutationstabelle, gesteuert wird. Die durch den „Apparat“ (durch Llulls Anweisungen) vorgegebenen Einschränkungen bewirken den grundlegenden Unterschied des llullschen Systems zu kabbalistischer Kombinatorik.

Geschichte

Die Große Kunst war Llull seinen Memoiren zufolge auf dem Berg Randa nahe Palma, wohin er sich 1274 zur Kontemplation zurückgezogen hatte, „von Gott offenbart“ worden (Vita coetanea, 1311). Er wurde von da an auch Doctor illuminatus genannt.

Ihre erste schriftliche Fassung erfuhr diese Kunst bald darauf in Ars compendiosa inveniendi veritatem, etwa Kurze Zusammenfassung der Kunst, die Wahrheit zu finden. In diesem und anderen Vorläufer-Werken beschrieb er ein weitaus komplizierteres System als später, mit bis zu 16 „Figuren“.

Die Wissenschaft unterscheidet mehrere Reifephasen des Werkes, deutlich aber zwei, nämlich 1274-89 und 1290-1308, bedingt durch Llulls Bemühen ab 1287, die Scholastiker der Universitäten von Montpellier und Paris von der Ars magna zu überzeugen. Dies erst hatte die Vereinfachung und Straffung zu dem System zur Folge, das in Ars generalis ultima vorgestellt wird.

1308 beendete Llull, annähernd parallel zur ausgereiften Ars generalis ultima, auch eine Kurzversion, die Ars brevis (mitunter auch Ars parva genannt).

Tafel der Prinzipien

	Figura A Principia absoluta	Figura T Principia relativa	Fragen Quaestiones	Subjekte (2) Subjecta	Tugenden Virtutes	Laster Vitia
B	bonitas	differentia	utrum? Ob?	Deus Das göttliche Sein	justitita	avaritia
C	magnitudo	concordantia	quid? Was?	angelus Das engelhafte Sein	prudentia	gula
D	duratio	contrarietas	de quo? Wovon?	caelum Das himmlische Sein	fortitudo	luxuria
E	potestas	principium	quare? Warum?	homo Das menschliche Sein	temperantia	superbia
F	sapientia	medium	quantum? Wie viel (wie groß)?	imaginatio	fides	accidia
G	voluntas	finis	quale? Wie beschaffen?	sensitiva Das sensible Sein	spes	invidia
H	virtus	majoritas	quando? Wann?	vegetativa Das vegetabile Sein	caritas	ira
I	veritas	aequalitas	ubi? Wo?	elementativa Das elementare Sein	patientia	mendacium
K	gloria	minoritas	quo modo? cum quo? Wie? Wozu?	instrumentativa	pietas	inconstantia

Die sechs Spalten zeigen neun absolute Prinzipien (in frühen Versionen von Llull als „göttliche Grade“ bezeichnet, später allgemeiner formuliert), und je neun relative Prinzipien, Fragestellungen, Subjekte, Tugenden und Laster (die beiden letzten Spalten werden zu Gegensatzpaaren zusammengefasst).

Die vier Figuren

Der Buchstabe A, alten Deutungen des Aleph zufolge für Gott stehend, bildet das Zentrum der ersten Figur: Die Ars Magna war für Llull medium persuasionis, also Werkzeug der Überzeugung, um Ungläubige durch (vermeintlich) zwingende Glaubensargumente zu bekehren.

Revolutionär war die vierte Figur, der (verständlicherweise) im Barock besondere Aufmerksamkeit gewidmet wurde: Drei und mehr konzentrische Kreisscheiben von abnehmender Größe liegen beweglich übereinander und erlauben dadurch 84 Kombinationen vom Typus BCD, BCE oder CDE. In der ersten Figur können als BCD-Kombination die Begriffe Güte, Größe und Ewigkeit nach dem Muster der aristotelischen Syllogistik miteinander verknüpft werden. Die von Llull beigefügte Tabelle enthält aber über die Dreibuchstabenkombination hinaus auch noch ein t, das den möglichen Wechsel zu einer anderen Tabellespalte anzeigt: Beispielsweise gelangt man von der Spalte der absoluten Prinzipien in die Spalte der relativen, indem man eine typische Frage voranstellt – also etwa die B-Frage ob? für Kombinationen, die mit B beginnen. Die Kombination BCtC führt dann zur Frage „Ob die Güte groß ist, sofern sie Übereinstimmendes enthält“ (nach Uta Kneller ⁽³⁾).

Folgewerke

• Llull selbst beendete 1308 Ars brevis, eine Kurzfassung des Hauptwerks.
• Erste bekannte Lullus-Interpretation ist Pico della Mirandolas Apologia, 1487.
• Giordano Bruno versucht den lullschen Ansatz zu erweitern, indem beispielsweise in De umbris idearum (Von den Schatten der Ideen) mehrere bewegliche konzentrische Räder vorschlägt, die mit je 30 Buchstaben eine gewaltige Vielfalt an Kombinationen erlauben würden.
• Gottfried Leibniz greift auf die Technik zurück, um philosophische Untersuchungen der Wissenschaften zu betreiben. Er benannte das Llullsche System ars combinatoria (in: Dissertatio de arte combinatoria, 1666)
• Athanasius Kircher beschreibt 1669 in Ars magna sciendi einen Weg, anhand llullscher Kombinatorik neue mathematische Erkenntnisse zu gewinnen.
• Heutigen Informatikern gilt Llulls Maschine als erster „Universalcomputer“, er selbst als Urahn der Informatik.

Anmerkungen

1. Die überzeugende Quelle Ramon Llull Database gibt 1305–1308 an.
2. Übersetzung der Tafel der Prinzipien nach Noack, zit. bei Friedrich Kirchner, Wörterbuch der philosophischen Grundbegriffe (1907), soweit passend.
3. Siehe Weblink zum Artikel von Uta Kneller

Literatur

• Raimundus Lullus: 'Ars brevis', übers. u. mit e. Einl. hrsg. von Alexander Fidora, Hamburg 1999

Weblinks

• http://quisestlullus.narpan.net/index.html Universität Barcelona, Ramon-Llull-Datenbank und umfangreiche Beschreibungen, Spanisch, Englisch; „Deutsch im Aufbau“.
• http://lullianarts.net/downloads.htm Englische Übersetzungen von Texten Llulls, und eine PC-Version der Ars magna.
• http://www-user.uni-bremen.de/~semiotik/lull.html Artikel von Uta Kneller