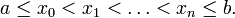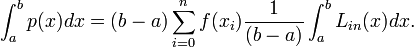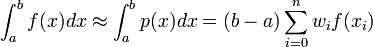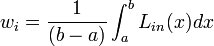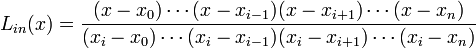- Newton-Cotes
-
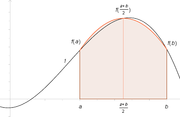
Eine Newton-Cotes-Formel (nach Isaac Newton und Roger Cotes) ist eine numerische Quadraturformel zur näherungsweisen Berechnung von Integralen. Diesen Formeln liegt die Idee zu Grunde, die zu integrierende Funktion durch ein Polynom zu interpolieren und dieses als Näherung exakt zu integrieren. Die Stützstellen der Interpolation werden dabei äquidistant gewählt.
Inhaltsverzeichnis
Herleitung
Zur numerischen Integration von
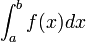 mit Hilfe einer Newton-Cotes-Formel wird das Intervall [a,b] in n gleich große Teilintervalle unterteilt. Dadurch erhält man n + 1 Stützstellen mit
mit Hilfe einer Newton-Cotes-Formel wird das Intervall [a,b] in n gleich große Teilintervalle unterteilt. Dadurch erhält man n + 1 Stützstellen mitGilt dabei a = x0 und b = xn, so spricht man von einer abgeschlossenen Newton-Cotes-Formel, andernfalls von einer offenen Newton-Cotes-Formel. Zur Herleitung nehmen wir ein Interpolationspolynom p der Funktion f zu den gegebenen Stützstellen. Für dieses gilt
mit Lin den Lagrange-Polynomen. Daraus folgt
Definition
Für die Newton-Cotes-Formel folgt dann
mit den Gewichten
Dabei bezeichnet Lin(x) das i-te Lagrange-Polynom. Die Gewichte sind symmetrisch, das heißt wn − i = wi. Ihre Summe ergibt immer eins.
Nach Konstruktion integrieren Newon-Cotes-Formeln Polynom bis zum Grad n exakt.
Abgeschlossene Newton-Cotes-Formeln
Abgeschlossene Newton-Cotes-Formeln von geradem Grad n haben die Eigenschaft, sogar Polynome vom Grad n+1 exakt zu integrieren.
Grad n Name Gewichte wi Fehlerschranke 0 Rechtecksregel 0 1 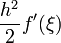
1 Trapezregel 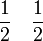
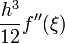
2 Simpson-Regel / Keplersche Fassregel 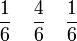
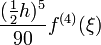
3 3/8 - Regel oder auch Pulcherrima 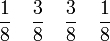
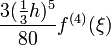
4 Milne-Regel 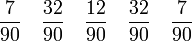
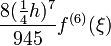
5 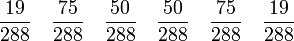
6 Weddle-Regel 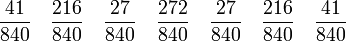
Für große n sind diese Formeln aus praktischer Sicht unbrauchbar, da viele Funktionswerte ausgewertet werden müssen. Dabei kommt es vermehrt zu Rundungsfehlern und Auslöschung. Ab n = 8 treten in etlichen Formeln sogar negative Gewichte auf.
Offene Newton-Cotes-Formeln
Grad n Name Stützstellen xi Gewichte wi Fehlerschranke 0 Mittelpunktsregel 
1 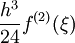
1 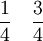
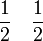
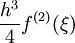
2 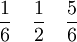
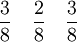
3 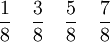
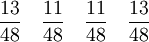
Literatur
- Hans R. Schwarz, Norbert Köckler: Numerische Mathematik. 6. Auflage, Teubner, Stuttgart 2006, ISBN 3-519-42960-8, S. 311–316
Wikimedia Foundation.