- Normtopologie
-
Dieser Artikel erklärt neben den gleichbedeutenden Begriffen normierter Raum und normierter Vektorraum per Weiterleitung auch die Begriffe Norm (Mathematik), Vektornorm, Halbnorm (Seminorm), Operatornorm, Matrixnorm und Frobeniusnorm. 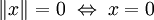 (Definitheit);
(Definitheit);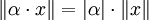 (Homogenität);
(Homogenität);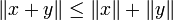 (die Dreiecksungleichung).
(die Dreiecksungleichung).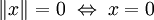 (Definitheit);
(Definitheit);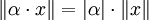 (Homogenität);
(Homogenität);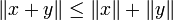 (die Dreiecksungleichung).
(die Dreiecksungleichung).- Aus der Homogenität folgt
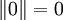 (d.h. in 1. ist eigentlich nur die Implikation „
(d.h. in 1. ist eigentlich nur die Implikation „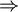 “ erforderlich) und
“ erforderlich) und 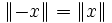 .
. - Wenn auf die Definitheit (Bedingung 1.) verzichtet wird, dann ist
 nur eine Halbnorm. Aus einem Raum mit Halbnorm erhält man einen normierten Raum als Faktorraum. Dazu werden Elemente x und y miteinander identifiziert, die
nur eine Halbnorm. Aus einem Raum mit Halbnorm erhält man einen normierten Raum als Faktorraum. Dazu werden Elemente x und y miteinander identifiziert, die 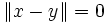 erfüllen. In der Funktionalanalysis betrachtet man neben den normierten Räumen auch Vektorräume mit einer Menge von Halbnormen und kommt so zum Begriff des lokalkonvexen Raums.
erfüllen. In der Funktionalanalysis betrachtet man neben den normierten Räumen auch Vektorräume mit einer Menge von Halbnormen und kommt so zum Begriff des lokalkonvexen Raums. - Wenn im Grundring R der Betrag durch einen Pseudobetrag ersetzt wird (d.h. die Multiplikativität von
 zur Submultiplikativität abgeschwächt wird) und im Modul M die Homogenität von
zur Submultiplikativität abgeschwächt wird) und im Modul M die Homogenität von  zur Subhomogenität abgeschwächt wird, erhält man den Begriff der Pseudonorm. Subhomogenität bedeutet, dass
zur Subhomogenität abgeschwächt wird, erhält man den Begriff der Pseudonorm. Subhomogenität bedeutet, dass 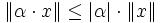 für alle Vektoren x und jeden Skalar α gilt.
für alle Vektoren x und jeden Skalar α gilt. 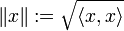
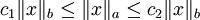 für alle
für alle 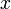 .
.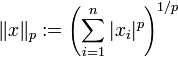
- Die 1-Norm
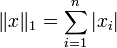
- Die 2-Norm
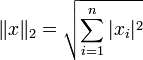
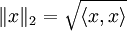
- Die
 -Norm
-Norm 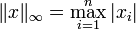
![\|x\|_p \leq \|x\|_1 \leq \sqrt[p\,]{n^{p-1}} \, \|x\|_p](/pictures/dewiki/48/09b6215fad769567265b8ab1f499ed6d.png) und
und![\|x\|_\infty \leq \|x\|_p \leq \sqrt[p\,]{n} \, \|x\|_{\infty}](/pictures/dewiki/101/e6cbb6628b47a306075c11151bc573b6.png) .
.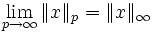
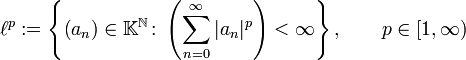
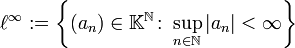
![\|(a_n)\|_p := \sqrt[p]{\sum_{n=0}^\infty |a_n|^p}](/pictures/dewiki/54/64cb50b806f26b0bde77c1a967a5726f.png)
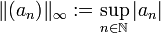
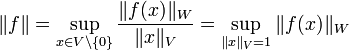 .
.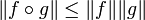 .
.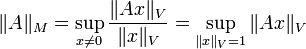 .
.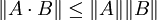
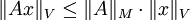
| normierter Raum |
|
berührt die Spezialgebiete |
|
hat die Eigenschaften von |
|
umfasst als Spezialfälle |
Der mathematische Begriff der Norm ist die Verallgemeinerung des geometrischen Begriffs der Länge eines Vektors. Eine Norm ist eine Funktion, die jedem Element eines Vektorraums eine nichtnegative reelle Zahl zuordnet und eine Reihe weiterer Eigenschaften (unter anderem die Dreiecksungleichung) erfüllt. Der Vektorraum, auf dem die Norm definiert ist, wird dann normierter Raum oder auch normierter Vektorraum genannt.
Dieser Normbegriff unterscheidet sich wesentlich vom Begriff der Norm in der Körpertheorie, er wird daher manchmal auch Vektornorm im Gegensatz zur Körpernorm genannt.
Inhaltsverzeichnis |
Formale Definition
Spezialfall reelle und komplexe Vektorräume
Sei V ein Vektorraum über dem Körper 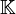 der reellen oder komplexen Zahlen. Eine Funktion
der reellen oder komplexen Zahlen. Eine Funktion 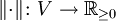 in die nichtnegativen reellen Zahlen heißt Norm auf V, wenn für alle Vektoren
in die nichtnegativen reellen Zahlen heißt Norm auf V, wenn für alle Vektoren 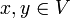 und alle Skalare
und alle Skalare 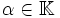 die folgenden axiomatischen Bedingungen erfüllt sind:
die folgenden axiomatischen Bedingungen erfüllt sind:
Ein Vektorraum V mit einer Norm 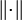 heißt normierter Vektorraum oder normierter Raum. Man schreibt dann
heißt normierter Vektorraum oder normierter Raum. Man schreibt dann 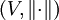 oder - wenn klar ist, um welche Norm es sich handelt - auch nur V.
oder - wenn klar ist, um welche Norm es sich handelt - auch nur V.
Allgemeiner Fall
Den Begriff einer Norm kann man wesentlich allgemeiner betrachten, indem man den Vektorraum V allgemeiner durch einen Modul M ersetzt:
Sei M ein R-(Links)-Modul über einem unitären Ring mit Betrag 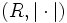 . Eine Funktion
. Eine Funktion 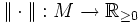 in die nichtnegativen reellen Zahlen heißt Norm auf M, wenn für alle
in die nichtnegativen reellen Zahlen heißt Norm auf M, wenn für alle 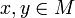 und alle Skalare
und alle Skalare 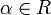 die folgenden axiomatischen Bedingungen erfüllt sind:
die folgenden axiomatischen Bedingungen erfüllt sind:
Bemerkungen
Einordnung
Jede Norm induziert durch 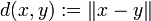 eine Metrik, jeder normierte Raum ist also auch ein metrischer Raum, und damit wiederum auch ein topologischer Raum. Diese durch die Norm definierte Topologie nennt man auch die Normtopologie. Für eine Folge (xn)n gilt
eine Metrik, jeder normierte Raum ist also auch ein metrischer Raum, und damit wiederum auch ein topologischer Raum. Diese durch die Norm definierte Topologie nennt man auch die Normtopologie. Für eine Folge (xn)n gilt 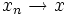 genau dann, wenn
genau dann, wenn 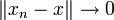 . Die Norm ist eine stetige Abbildung in Bezug auf die durch sie induzierte Topologie.
. Die Norm ist eine stetige Abbildung in Bezug auf die durch sie induzierte Topologie.
Eine Norm kann, muss aber nicht, durch ein inneres Produkt (Skalarprodukt) 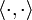 definiert sein. Jeder Innenproduktraum ist mit
definiert sein. Jeder Innenproduktraum ist mit
ein normierter Raum. Allgemein nennt man eine durch ein Skalarprodukt induzierte Norm auch Hilbertnorm.
Ein normierter Raum heißt vollständig, wenn jede Cauchy-Folge in diesem Raum einen Grenzwert besitzt. Ein vollständiger normierter Raum heißt Banachraum, und ein vollständiger normierter Innenproduktraum heißt Hilbertraum.
Äquivalenz von Normen
Zwei Normen 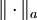 und
und 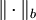 heißen äquivalent, wenn es positive Konstanten
heißen äquivalent, wenn es positive Konstanten 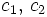 gibt mit
gibt mit
Äquivalente Normen induzieren dieselbe uniforme Struktur und damit erst recht dieselbe Topologie.
Auf einem endlichdimensionalen Vektorraum, also z.B. auf  , sind alle Normen äquivalent.
, sind alle Normen äquivalent.
Betragsnormen
Normen auf Körpern (siehe z.B. p-adische Zahlen) sind die absoluten Beträge.
Vektornormen
p-Normen
Für endlichdimensionale Räume 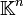 sind die so genannten p-Normen definiert als:
sind die so genannten p-Normen definiert als:
Dabei ist 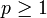 eine reelle Zahl und | xi | der Absolutbetrag der i-ten Koordinate des Vektors x. Die aus diesen Normen abgeleiteten Metriken heißen auch Minkowski-Metriken. Für p < 1 können so keine Normen definiert werden, da dann die Dreiecksungleichung verletzt ist.
eine reelle Zahl und | xi | der Absolutbetrag der i-ten Koordinate des Vektors x. Die aus diesen Normen abgeleiteten Metriken heißen auch Minkowski-Metriken. Für p < 1 können so keine Normen definiert werden, da dann die Dreiecksungleichung verletzt ist.
p = 1: Betragssummennorm
heißt auch Betragssummennorm; die von ihr abgeleitete Metrik heißt speziell im zweidimensionalen Raum 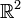 auch Taxi-, City-Block- oder Manhattan-Metrik, da sie den Abstand zweier Punkte wie die Fahrtstrecke auf einem Stadtplan im Schachbrett-Format misst, auf dem man sich nur in senkrechten und waagerechten Abschnitten bewegen kann.
auch Taxi-, City-Block- oder Manhattan-Metrik, da sie den Abstand zweier Punkte wie die Fahrtstrecke auf einem Stadtplan im Schachbrett-Format misst, auf dem man sich nur in senkrechten und waagerechten Abschnitten bewegen kann.
p = 2: Euklidische Norm
heißt auch Euklidische Norm; ein mit der 2-Norm versehener Vektorraum wird ein Euklidischer Raum genannt. Im 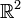 und
und  beschreibt die euklidische Norm die anschauliche Länge eines Vektors und führt über die induzierte euklidische Metrik zu dem uns gewohnten Abstandsbegriff. Die Menge aller Vektoren mit Norm 1 bildet im
beschreibt die euklidische Norm die anschauliche Länge eines Vektors und führt über die induzierte euklidische Metrik zu dem uns gewohnten Abstandsbegriff. Die Menge aller Vektoren mit Norm 1 bildet im 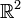 den Einheitskreis, im
den Einheitskreis, im  die Einheitskugel und allgemein im
die Einheitskugel und allgemein im  die n-dimensionale Einheitssphäre. Die euklidische Norm ist die durch das Euklidische Skalarprodukt induzierte Norm:
die n-dimensionale Einheitssphäre. Die euklidische Norm ist die durch das Euklidische Skalarprodukt induzierte Norm:
p → ∞: Maximumsnorm
heißt auch Maximumsnorm oder Tschebyschow-Norm. Sie ist formal keine p-Norm, kann aber als Grenzfall für 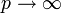 aufgefasst werden, wie im folgenden Abschnitt gezeigt wird:
aufgefasst werden, wie im folgenden Abschnitt gezeigt wird:
Zusammenhänge zwischen den p-Normen
Als Normen auf endlichdimensionalen Vektorräumen sind alle p-Normen inklusive der Maximumsnorm zueinander äquivalent; als eingrenzende Faktoren ergeben sich, wenn n die Dimension des Vektorraums ist:
Aus der zweiten Zeile folgt der schon durch die Bezeichnungen angedeutete Zusammenhang
Außerdem gilt für 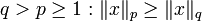 . Die Norm ist für wachsendes p monoton fallend.
. Die Norm ist für wachsendes p monoton fallend.
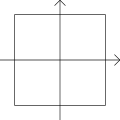
Veranschaulichung in der euklidischen Ebene
Zur Veranschaulichung betrachten wir zweidimensionale Vektoren 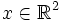 . Die Menge aller Einheitsvektoren
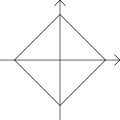
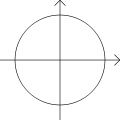
. Die Menge aller Einheitsvektoren 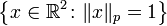 bildet einen verallgemeinerten Einheitskreis, er fällt nur für p = 2 mit dem in der Geometrie betrachteten Kreisbegriff zusammen. Mit den Normen zu p=1, p=2 und p=∞ ergeben sich in einem kartesischen Koordinatensystem folgende Darstellungen der Einheitskreise:
bildet einen verallgemeinerten Einheitskreis, er fällt nur für p = 2 mit dem in der Geometrie betrachteten Kreisbegriff zusammen. Mit den Normen zu p=1, p=2 und p=∞ ergeben sich in einem kartesischen Koordinatensystem folgende Darstellungen der Einheitskreise:
lp-Normen
Die „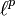 -Normen“ sind eine Verallgemeinerung der p-Normen auf spezielle unendlichdimensionale Vektorräume.
-Normen“ sind eine Verallgemeinerung der p-Normen auf spezielle unendlichdimensionale Vektorräume.
Wir gehen zunächst von der Menge 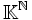 aller Zahlenfolgen in einem Körper (z.B.
aller Zahlenfolgen in einem Körper (z.B. 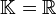 ) aus. Dabei wollen wir die Null als zu
) aus. Dabei wollen wir die Null als zu 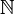 gehörend ansehen. Für eine reelle Zahl
gehörend ansehen. Für eine reelle Zahl 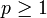 bzw. das Symbol
bzw. das Symbol 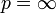 betrachten wir die Teilmengen
betrachten wir die Teilmengen
aller „in p-ter Potenz summierbaren Folgen“ bzw. aller beschränkten Folgen. Die so erklärten Teilmengen 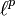 sind
sind 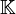 -Vektorräume, auf denen man die so genannte lp-Norm wie folgt definiert:
-Vektorräume, auf denen man die so genannte lp-Norm wie folgt definiert:
Versehen mit diesen Normen werden die Vektorräume 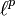 zu vollständigen normierten Räumen.
zu vollständigen normierten Räumen.
Lp-Normen
Die Definition der Lp-Räume und -Normen wird hier nur kurz angerissen, ausführlichere Informationen dazu finden sich im Artikel Lp-Raum.
Analog zu den Folgenräumen kann man den Vektorraum der Funktionen 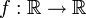 betrachten, und darin die "in p-ter Potenz integrierbaren Funktionen" herausgreifen, für die man so genannte Lp-Normen definiert. Das ist jedoch zunächst nur eine Halbnorm, da
betrachten, und darin die "in p-ter Potenz integrierbaren Funktionen" herausgreifen, für die man so genannte Lp-Normen definiert. Das ist jedoch zunächst nur eine Halbnorm, da 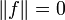 nicht ausschließlich für die Nullfunktion gilt. Man geht deshalb über zu einem Faktorraum (den man Lp nennt), auf dem die Lp-Halbnorm dann eine Norm induziert.
nicht ausschließlich für die Nullfunktion gilt. Man geht deshalb über zu einem Faktorraum (den man Lp nennt), auf dem die Lp-Halbnorm dann eine Norm induziert.
Operatornormen
Für einen linearen Operator 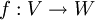 wird seine Operatornorm (anschaulich der größtmögliche Streckungsfaktor) bezüglich der Vektornormen folgendermaßen definiert:
wird seine Operatornorm (anschaulich der größtmögliche Streckungsfaktor) bezüglich der Vektornormen folgendermaßen definiert:
Ist 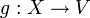 ein weiterer linearer Operator so sind die jeweiligen Operatornormen zusätzlich zu den üblichen Normeigenschaften submultiplikativ:
ein weiterer linearer Operator so sind die jeweiligen Operatornormen zusätzlich zu den üblichen Normeigenschaften submultiplikativ:
Dabei ist die Operatornorm von linearen Abbildungen zwischen endlich-dimensionalen Vektorräumen stets endlich, da die Einheitskugel eine kompakte Menge ist, und damit eine echte Norm. In unendlich-dimensionalen Vektorräumen ist dies nicht immer gegeben. Operatoren, deren Norm unendlich als Wert annimmt, werden unbeschränkt genannt. Dabei handelt es sich streng genommen nicht mehr um Normen im obigen Sinne. Man kann zeigen, dass ein linearer Operator zwischen normierten Räumen genau dann eine endliche Operatornorm hat, wenn er stetig ist.
Matrixnormen
Für reelle oder komplexe Matrizen können verschiedene Normen angegeben werden, wobei in der Literatur teilweise die Submultiplikativität als weitere definierende Eigenschaft verlangt wird. Es gibt jedoch Matrixnormen mit den üblichen Normeigenschaften, die nicht submultiplikativ sind. Eine Matrixnorm kann von einer Vektornorm induziert oder mit verschiedenen Vektornormen verträglich sein.
Eine Matrixnorm 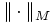 heißt induziert von einer Vektornorm
heißt induziert von einer Vektornorm 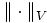 , wenn sie von ihr in der oben beschriebenen Weise (als Operatornorm) abgeleitet ist, falls also gilt:
, wenn sie von ihr in der oben beschriebenen Weise (als Operatornorm) abgeleitet ist, falls also gilt:
Dabei wird das Supremum angenommen (sup kann durch max ersetzt werden), weil die Normabbildung stetig und die Menge der Einheitsvektoren (im endlichdimensionalen Vektorraum 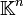 ) kompakt ist.
) kompakt ist.
Als Operatornorm ist eine induzierte Matrixnorm stets submultiplikativ, mit Matrizen ausgedrückt gilt also:
Eine Matrixnorm 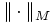 heißt mit einer Vektornorm
heißt mit einer Vektornorm 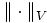 verträglich, wenn gilt:
verträglich, wenn gilt:
Offensichtlich ist die von einer Vektornorm induzierte Matrixnorm mit dieser Vektornorm verträglich.
Matrixnormen haben einige nützliche Eigenschaften, so ist beispielsweise der Spektralradius einer Matrix (der betragsgrößte Eigenwert) niemals größer als der Wert einer beliebigen submultiplikativen Matrixnorm. Sie werden insbesondere in der numerischen Mathematik benutzt.
Beispiele für Matrixnormen
| Name | Definition | Zusammenhänge mit Vektornormen |
|---|---|---|
| Spaltensummennorm | 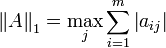 |
induziert durch Betragssummennorm |
| Spektralnorm | 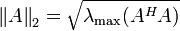 , ,wobei AH die adjungierte (oder hermitesierte) Matrix und λmax den betragsmäßig größten Eigenwert des Matrixprodukts AHA bezeichnet. |
induziert durch Euklidische Norm |
| Zeilensummennorm | 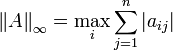 |
induziert durch Maximumsnorm |
| Gesamtnorm | 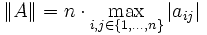 |
verträglich mit Betragssummennorm, Euklidischer Norm, Maximumsnorm |
| Frobeniusnorm | 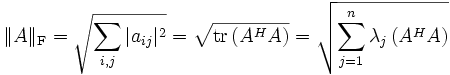 , ,
wobei |
verträglich mit Euklidischer Norm |
Ein Beispiel für eine nicht submultiplikative Matrixnorm ist 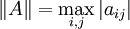 .
.
Weitere Matrixnormen sind die Ky-Fan-Normen.
Wikimedia Foundation.

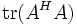 die
die 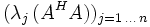 die Liste aller
die Liste aller