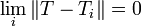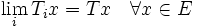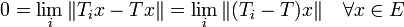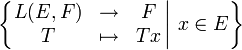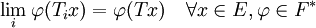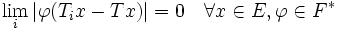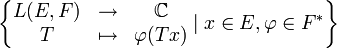- Starke Operatortopologie
-
Der Begriff Linearer Operator wurde in der Funktionalanalysis (einem Teilgebiet der Mathematik) eingeführt und ist synonym zum Begriff der linearen Abbildung. Eine lineare Abbildung ist eine strukturerhaltende Abbildung zwischen Vektorräumen über einem gemeinsamen Körper. Werden Vektorräume über dem Körper der reellen oder komplexen Zahlen betrachtet und sind diese mit einer Topologie versehen (lokalkonvexe Räume, normierte Räume, Banachräume), so spricht man vorzugsweise von linearen Operatoren.
Man unterscheidet zwischen beschränkten und unbeschränkten linearen Operatoren.
Inhaltsverzeichnis
Definition
Es seien X und Y reelle oder komplexe Vektorräume. Ein Operator T von X in Y heißt linearer Operator, wenn für alle
 und
und 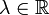 (bzw.
(bzw. 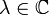 ) die folgenden Bedingungen gelten:
) die folgenden Bedingungen gelten:- T ist homogen: T(λx) = λT(x)
- T ist additiv: T(x + y) = T(x) + T(y).
Antilinearer Operator
Seien X und Y komplexe Vektorräume. Ein Operator T von X in Y heißt antilinearer Operator, wenn für alle
 und
und 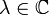 die folgenden Bedingungen gelten:
die folgenden Bedingungen gelten:- T ist antihomogen:
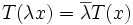
- T ist additiv: T(x + y) = T(x) + T(y).
Beispiele linearer Operatoren
- Es sei A eine reelle
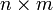 -Matrix. Dann ist die lineare Abbildung
-Matrix. Dann ist die lineare Abbildung 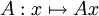 ein linearer Operator von
ein linearer Operator von 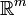 in
in  .
.
- Jedes lineare Funktional auf einem Vektorraum ist ein linearer Operator.
- Die Menge der linearen Operatoren zwischen zwei fixierten Vektorräumen wird durch die Definition der Addition (S + T)(x): = S(x) + T(x) und skalaren Multiplikation (λS)(x): = λS(x) selbst zu einem Vektorraum.
- Der Ableitungsoperator, der einer Funktion ihre Ableitung zuordnet
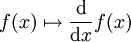 ist ein linearer Operator.
ist ein linearer Operator.
- Der Integraloperator
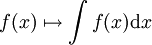 ist ein linearer Operator.
ist ein linearer Operator.
Beispiel einer antilinearen Abbildung
Ist H ein komplexer Hilbertraum und
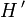 sein Dualraum, so gibt es nach dem rieszschen Darstellungssatz zu jedem
sein Dualraum, so gibt es nach dem rieszschen Darstellungssatz zu jedem 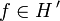 genau ein
genau ein 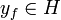 , so dass
, so dass 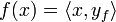 für alle
für alle 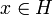 gilt. Die Abbildung
gilt. Die Abbildung 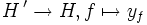 ist antilinear.
ist antilinear.Bedeutung und Anwendungen
Die Bedeutung linearer Operatoren besteht darin, dass sie die lineare Struktur des unterliegenden Raumes respektieren, d.h. sie sind Homomorphismen zwischen Vektorräumen.
Anwendungen linearer Operatoren sind:
- Die Beschreibung von Koordinatentransformationen im dreidimensionalen Euklidischen Raum (Spiegelung, Drehung, Streckung) und der Lorentztransformation in der vierdimensionalen Raumzeit durch Matrizen.
- Die Darstellung von Observablen in der Quantenmechanik und die Beschreibung der Dynamik eines quantenmechanischen Systems durch seinen Hamilton-Operator H in der Schrödingergleichung.
- Die Entwicklung von Lösungstheorien für Differential- und Integralgleichungen, siehe Sobolew-Raum und Distribution.
- In der Vierpoltheorie (Elektrotechnik) werden die Beziehungen zwischen den Eingangsgrößen (Stromstärke und Spannung) und den Ausgangsgrößen (Stromstärke und Spannung) als wechselseitig voneinander linear abhängig betrachtet werden. Die Abhängigkeiten können durch 2x2 Matrizen beschrieben werden.
Beschränkte lineare Operatoren
Betrachten wir zwei normierte Räume V und W und eine lineare Abbildung
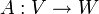 . Die Operatornorm von A ist definiert durch:
. Die Operatornorm von A ist definiert durch: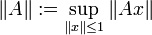 .
.
Ist die Operatornorm endlich, so heißt der Operator beschränkt, andernfalls unbeschränkt.
Die Menge aller beschränkten linearen Operatoren vom normierten Raum V in den normierten Raum W nennt man
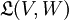 . Falls V mit W identisch ist, wird auch abkürzend
. Falls V mit W identisch ist, wird auch abkürzend 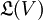 geschrieben. Die beschränkten linearen Operatoren lassen sich wie folgt charakterisieren:
geschrieben. Die beschränkten linearen Operatoren lassen sich wie folgt charakterisieren:Ist T ein linearer Operator aus
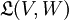 , dann sind die folgenden Aussagen äquivalent:
, dann sind die folgenden Aussagen äquivalent:- T ist beschränkt.
- T ist stetig in jedem Punkt von V.
- T ist stetig im Nullpunkt von V.
Beispiele beschränkter linearer Operatoren
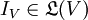 mit
mit 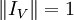 , wobei IV der Identische Operator auf V ist.
, wobei IV der Identische Operator auf V ist.
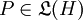 mit
mit 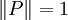 , wobei P eine orthogonale Projektion auf dem Hilbertraum H ist.
, wobei P eine orthogonale Projektion auf dem Hilbertraum H ist.
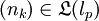 mit
mit 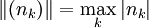 , wobei die Folge (nk) beschränkt ist und als Diagonaloperator auf dem Folgenraum lp mit
, wobei die Folge (nk) beschränkt ist und als Diagonaloperator auf dem Folgenraum lp mit 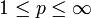 interpretiert wird.
interpretiert wird.
- Der Shiftoperator
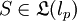 ist beschränkt mit
ist beschränkt mit 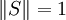 , wobei
, wobei  auf dem Folgenraum lp mit
auf dem Folgenraum lp mit 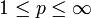 definiert ist.
definiert ist.
- Es sei K eine kompakte Menge und
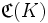 der Banachraum der stetigen Funktionen auf K mit der Supremumsnorm. Weiter sei
der Banachraum der stetigen Funktionen auf K mit der Supremumsnorm. Weiter sei 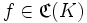 und der lineare Operator
und der lineare Operator 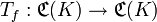 ist definiert durch Tf(g)(k): = (fg)(k) für
ist definiert durch Tf(g)(k): = (fg)(k) für 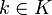 . Dann ist
. Dann ist 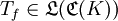 und
und 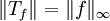 .
.
- Es sei
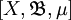 ein Maßraum und
ein Maßraum und 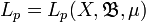 der Banachraum der p-integrablen messbaren Funktionen, Lp-Raum oder Lebesgue-Raum, (Äquivalenzklassen von Funktionen) auf X mit der p-Norm für
der Banachraum der p-integrablen messbaren Funktionen, Lp-Raum oder Lebesgue-Raum, (Äquivalenzklassen von Funktionen) auf X mit der p-Norm für 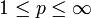 . Weiter sei
. Weiter sei 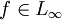 und der lineare Operator
und der lineare Operator 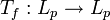 ist definiert durch Tf(g)(x): = (fg)(x) für
ist definiert durch Tf(g)(x): = (fg)(x) für  . Dann ist
. Dann ist 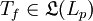 und
und 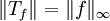 .
.
Anwendungen
- Funktionalkalkül, d.h. für eine beschränkte, reelle bzw. komplexwertige messbare Funktion f und einem beschränkten linearen Operator T kann f(T) definiert werden.
Unbeschränkte lineare Operatoren
Der Definitionsbereich eines unbeschränkten linearen Operators ist im allgemeinen ein linearer Unterraum eines topologischen Vektorraums und der Operator wird in diesem Fall als eine partielle lineare Abbildung aufgefasst. Der Definitionsbereich eines Operators wird als Domäne bezeichnet.
Ein Operator heißt dicht definiert, wenn seine Domäne eine dichte Teilmenge des Ausgangsraumes ist. Das Interesse an unbeschränkten Operatoren ist durch die Untersuchung von Differentialoperatoren und deren Eigenwertspektrum und Observablenalgebren begründet.
Eine große Klasse unbeschränkter linearer Operatoren bilden die abgeschlossenen Operatoren. Das sind Operatoren
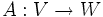 deren Graph
deren Graph 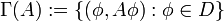 in der Produkttopologie von
in der Produkttopologie von 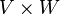 abgeschlossen ist. Für abgeschlossene Operatoren kann z. B. das Spektrum definiert werden.
abgeschlossen ist. Für abgeschlossene Operatoren kann z. B. das Spektrum definiert werden.Beispiel
Betrachte den Differentialoperator
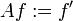 auf dem Banachraum C[a,b] der stetigen Funktion auf dem Interval [a,b]. Wählt man als Definitionsbereich
auf dem Banachraum C[a,b] der stetigen Funktion auf dem Interval [a,b]. Wählt man als Definitionsbereich 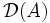 die einmal stetig differenzierbaren Funktionen
die einmal stetig differenzierbaren Funktionen ![\mathcal{D}(A):=C^{1}[a, b]](/pictures/dewiki/51/37ebffc160075b2f2c97d9a2f3be4de8.png) , dann ist A ein abgeschlossener Operator, der nicht beschränkt ist.
, dann ist A ein abgeschlossener Operator, der nicht beschränkt ist.Anwendungen
- Differential- und Multiplikationsoperatoren sind i. a. unbeschränkt.
- Die Darstellung von Observablen der Quantenmechanik erfordert unbeschränkt lineare Operatoren, da die den Observablen zugeordneten Operatoren i. a. unbeschränkt sind.
Konvergenzbegriffe / Topologien auf Operatorräumen
Ist der zugrundeliegende Vektorraum endlichdimensional mit Dimension n, so ist L(V) ein Vektorraum der Dimension n2. In diesem Fall sind alle Normen äquivalent. d.h. sie liefern den gleichen Konvergenzbegriff und die gleiche Topologie.
Im Unendlichdimensionalen gibt es dagegen verschiedene nicht-äquivalente Topologien. Seien nun E und F Banachräume und
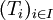 eine Folge (oder auch ein Netz) in L(E,F).
eine Folge (oder auch ein Netz) in L(E,F).Normtopologie
Ti konvergiert in der Normtopologie gegen T genau dann wenn:
Die Normtopologie ist die Topologie, die durch die offenen Kugeln erzeugt wird.
Starke Operatortopologie
Ti konvergiert in der starken Operatortoplogie (kurz stop) gegen T genau dann wenn:
oder anders ausgedrückt:
Die zugehörige Topologie ist die Initialtopologie, die durch die Menge von linearen Abbildungen
erzeugt wird. Dies ist die kleinste Topologie, in der all diese Abbildungen stetig sind. L(E,F) mit der starken Operatortoplogie ist also ein lokal konvexer Raum.
Schwache Operatortopologie
Ti konvergiert in der schwachen Operatortoplogie gegen T genau dann wenn:
oder anders ausgedrückt:
(Hierbei bezeichnet F * den stetigen Dualraum von F)
Die zugehörige Topologie ist die Initialtopologie, die durch die Menge von linearen Funktionalen
erzeugt wird. Dies ist die kleinste Topologie, in der all diese Funktionale stetig sind. L(E,F) mit der schwachen Operatortoplogie ist also ebenfalls ein lokal konvexer Raum.
Literatur
- Hans Wilhelm Alt: Lineare Funktionalanalysis : eine anwendungsorientierte Einführung. 5. Auflage. Springer-Verlag, 2006, ISBN 3-540-34186-2
Wikimedia Foundation.