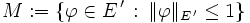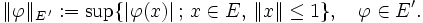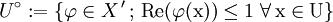Satz von Alaoglu

Der Satz von Banach-Alaoglu (auch Satz von Alaoglu oder Satz von Alaoglu-Bourbaki bzw. in einer allgemeineren Version Satz von Banach-Alaoglu-Bourbaki) ist ein Kompaktheitssatz und wird im Allgemeinen dem Gebiet der Funktionalanalysis zugeordnet, obwohl er eine rein topologische Aussage enthält und im Wesentlichen aus dem Satz von Tychonoff folgt.

Der Satz

Es sei E ein normierter Raum. Dann ist die Menge

$M := \{\varphi \in E^{\,\prime}\,:\,\|\varphi\|_{E^{\,\prime}} \leq 1\}$

kompakt bezüglich der schwach-*-Topologie in 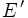$E^{\,\prime}$, wobei 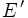$E^{\,\prime}$ den topologischen Dualraum von E bezeichnet.

Diskussion

Die Bedeutung dieser Aussage ergibt sich vor allem aus dem Vergleich mit dem Lemma von Riesz, wonach die normabgeschlossene Einheitskugel eines normierten Raumes genau dann kompakt bezüglich der Normtopologie ist, wenn der Raum endliche Dimension hat. Der topologische Dualraum 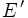$E^{\,\prime}$, also der Raum aller stetigen linearen Funktionale auf einem normierten Raum E, ist selbst wieder normiert vermöge

$\|\varphi\|_{E^{\,\prime}} := \sup\{|\varphi(x)|\,;\,x \in E, \, \|x\| \leq 1\}, \quad \varphi \in E'.$

Die normabgeschlossene Einheitskugel in 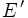$E^{\,\prime}$ ist gerade die Menge M. Mit E ist auch 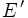$E^{\,\prime}$ von unendlicher Vektorraum-Dimension. Angewandt auf 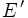$E^{\,\prime}$ folgt aus dem Lemma von Riesz, dass M im Fall 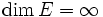$\dim E = \infty$ nicht normkompakt ist. Wohl aber ist M kompakt in der schwächeren schwach-*-Topologie.

Man beachte an dieser Stelle nochmals, dass zur Konstruktion von M die Norm von 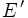$E^{\,\prime}$ verwendet wird, die Kompaktheit aber nicht inder Normtopologie, sondern in der schwach-*-Topologie gilt.

Im Zusammenhang mit obigem Vergleich lässt sich auch die Einordnung des Satzes von Banach-Alaoglu in den Bereich der Funktionalanalysis begründen, denn erst bei unendlicher Dimension des zugrunde liegenden normierten Raumes ist die Aussage nichttrivial (E und 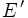$E^{\,\prime}$ mit obiger Norm sind im Endlichdimensionalen topologisch isomorph, und die schwach-*-Topologie ist gleich der Normtopologie).

Anwendung

Kompakte Mengen sind in der (Funktional-)Analysis immer von großer Bedeutung. Da sie in unendlichdimensionalen normierten Räumen (nach dem oben genannten Lemma von Riesz) eher rar sind und der Wechsel zu der schwächeren *-Topologie aber in vielen Situationen keine große Einschränkung bedeutet bzw. diese Topologie auf natürlichem Wege ins Spiel kommt, gibt einem dieser Satz eine Fülle „neuer“ kompakter Mengen an die Hand. Als prominentes Beispiel soll hier der Beweis des Satzes von Gelfand und Neumark aus der Theorie der C*-Algebren genannt werden, der einen isometrischen Isomorphismus zwischen einer C*-Algebra A und den stetigen Funktionen C(Γ_A) auf einer kompakten Menge Γ_A herstellt. Die Kompaktheit der Menge Γ_A folgt dabei aus einer Anwendung des Satzes von Banach-Alaoglu.

Verallgemeinerungen und andere Formulierungen

Verallgemeinerung: Satz von Alaoglu-Bourbaki

Der Satz von Banach-Alaoglu kann für allgemeinere Vektorräume formuliert werden.

Sei X ein lokal konvexer Raum. Für eine Nullumgebung U in X ist

$U^{\circ} := \{\varphi \in X^{\,\prime}\,;\,\rm{Re}(\varphi(x)) \leq 1\ \forall\,x \in U\}$

(die sog. Polare von U) eine 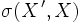$\sigma(X^{\,\prime},X)$-kompakte Menge.

Für Banachräume

Die Einheitskugel 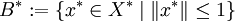$B^*:=\{ x^*\in X^*\mid \|x^*\| \leq 1\}$ im Dualraum X ^* eines Banachraumes X ist schwach-*-kompakt.

Für separable Banachräume

Die Einheitskugel 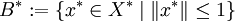$B^*:=\{ x^*\in X^*\mid \|x^*\| \leq 1\}$ im Dualraum X ^* eines separablen Banachraumes X ist mit der schwach-*-Topologie kompakt und metrisierbar.

Literatur

• Dirk Werner: Funktionalanalysis. Springer, Berlin 1995, ISBN 3-540-59168-0, S. 335 f.
• Herbert Schröder: Funktionalanalysis. 2. Auflage. Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1623-3, S. 93 f.
• Klaus Jänich: Topologie. 4. Auflage. Springer, Berlin 1994, ISBN 3-540-57471-9, S. 201 f.